Bài tập tự luyện
-
1278 lượt thi
-
19 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
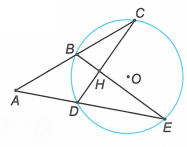
Cho tam giác ABC, vẽ đường tròn tâm O đi qua A và tiếp xúc với BC tại B. Kẻ dây BD song song với AC. Gọi I là giao điểm của CD với đường tròn.
Chứng minh .
 Xem đáp án
Xem đáp án
Ta có: (cùng chắn cung ).
Mặt khác nên (so le trong).
Do đó .
Câu 2:
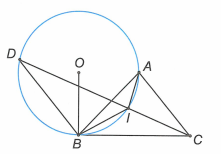
Cho hai đường tròn và cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn cắt tại C và tiếp tuyến tại A của đường tròn cắt tại D.
Chứng minh .
 Xem đáp án
Xem đáp án
Trong đường tròn có (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn ).
Tương tự trong đường tròn ta cũng có .
Xét và có và nên .
Câu 3:
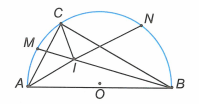
Cho nửa đường tròn (O) đường kính AB và dây AC căng cung AC có số đo bằng 60 độ.
a) So sánh các góc của tam giác ABC.
 Xem đáp án
Xem đáp án
a) Tam giác có: (góc nội tiếp chắn nửa đường tròn).
.
Vậy .
Câu 4:
b) Gọi M, N lần lượt là điểm chính giữa của các cung AC và BC. Hai dây AN và BM cắt nhau tại I. Chứng minh rằng tia CI là tia phân giác của góc ACB.
 Xem đáp án
Xem đáp án
b) Vì là điểm chính giữa của cung AC và BC nên các tia AN,BM là các tia phân giác của các góc A và B. Mà AN và BM cắt nhau tại I nên CI là đường phân giác thứ ba của tam giác ABC hay CI là tia phân giác của góc ACB.
Câu 5:
Cho tam giác ABC cân tại A( góc A < 90 độ). Vẽ đường tròn đường kính AB cắt BC tại D, cắt AC tại E. Chứng minh rằng:
a) Tam giác DBE cân.
 Xem đáp án
Xem đáp án
a) (góc nội tiếp chắn nửa đường tròn)
là trung điểm BC (do cân).
Tam giác EBC vuông tại E có ED là đường trung tuyến ứng với cạnh huyền BC nên .
Vậy tam giác DBE cân.
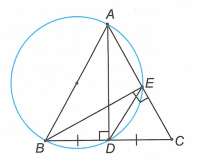
Câu 7:
Cho tam giác nội tiếp trong đường tròn (O). Vẽ đường kính (điểm M thuộc cung BC không chứa A). Chứng minh rằng các tia AM, AN lần lượt là các tia phân giác trong và ngoài tại đỉnh A của tam giác ABC.
 Xem đáp án
Xem đáp án
Vì nên M là điểm chính giữa của cung
. Do đó AM là tia phân giác của góc BAC.
Ta có: (góc nội tiếp chắn nửa đường tròn). (1)
. (2)
Từ (1) và (2) suy ra là tia phân giác của góc ngoài tại đỉnh A của tam giác ABC.
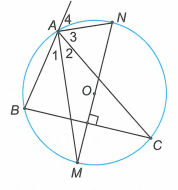
Câu 8:
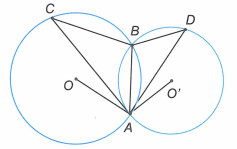
Cho đường tròn và hai dây vuông góc với nhau. Gọi lần lượt là điểm chính giữa của các cung nhỏ MA và MB. Gọi P là giao điểm của AK và BI.
a) Chứng minh rằng ba điểm A,O,B thẳng hàng.
 Xem đáp án
Xem đáp án
a) Gọi .
Vì I,K lần lượt là điểm chính giữa của cung nên . Suy ra là hình chữ nhật.
Ta có:
thẳng hàng.
Câu 9:
b) Chứng minh rằng P là tâm đường tròn nội tiếp tam giác MAB.
 Xem đáp án
Xem đáp án
b) Dễ thấy AK và BI lần lượt là tia phân giác của góc .
Mà P là giao điểm của AK và BI nên P là tâm đường tròn nội tiếp tam giác MAB.
Câu 10:
c) Giả sử MA=12cm, MB=16cm, tính bán kính của đường tròn nội tiếp tam giác MAB
 Xem đáp án
Xem đáp án
c) Áp dụng định lí Pitago trong tam giác vuông MAB ta được AB=20cm.
Ta có: .
Mà .
Câu 11:
Cho tam giác ABC nội tiếp đường tròn (O), hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF.
a) Tứ giác BFCH là hình gì?
 Xem đáp án
Xem đáp án
a) Ta có (góc nội tiếp chắn nửa đường tròn).
Suy ra
(cùng vuông góc với AB).
(cùng vuông góc với AC).
Do đó là hình bình hành.
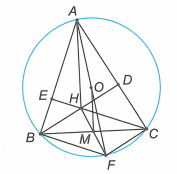
Câu 12:
b) Gọi M là trung điểm BC. Chứng minh rằng ba điểm H,M,F thẳng hàng.
 Xem đáp án
Xem đáp án
b) Do là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường. Mà M là trung điểm của BC nên M cũng là trung điểm của HF.
Vậy H,M,F thẳng hàng.
Câu 13:
c) Chứng minh rằng .
 Xem đáp án
Xem đáp án
c) Vì M là trung điểm của BC nên (quan hệ đường kính và dây cung) (1)
Lại có H là trực tâm của nên . (2)
Từ (1) và (2) suy ra . Mặt khác, M là trung điểm của BC nên OM là đường trung bình của tam giác AHF. Do đó .
Câu 14:
Cho đường tròn (O) đường kính AB, M là điểm chính giữa của một nửa đường tròn. C là điểm bất kì trên nửa đường tròn kia, CM cắt AB tại D. Vẽ dây AE vuông góc với CM tại F.
a) Chứng minh rằng tứ giác ACEM là hình thang cân.
 Xem đáp án
Xem đáp án
a) Ta có (vì M là điểm chính giữa của ).
Do đó là tam giác vuông cân.
Tương tự, ta cũng có là tam giác vuông cân.
(hai góc ở vị trí so le trong).
Suy ra là hình thang.
Dễ thấy nên là hình thang cân.
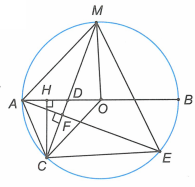
Câu 15:
b) Vẽ CH vuông góc với AB. Chứng minh rằng tia CM là tia phân giác của góc HCO.
 Xem đáp án
Xem đáp án
b) Tam giác cân tại O (vì OC=OM).
(1)
Vì M là điểm chính giữa của nên . Mà .
Suy ra (hai góc so le trong) (2)
Từ (1) và (2) suy ra là tia phân giác của góc .
Câu 16:
c) Chứng minh rằng .
 Xem đáp án
Xem đáp án
c) Ta có .
Vì M là điểm chính giữa của một nửa đường tròn, C là điểm bất kì trên nửa đường tròn kia nên
(do là hình thang cân).
Vậy .
Câu 17:
Cho đường tròn (O) và một dây AB. Vẽ đường kính CD vuông góc với AB (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm N. Các đường thẳng CN và DN lần lượt cắt đường thẳng AB tại F và E. Tiếp tuyến của đường tròn (O) tại N cắt đường thẳng AB tại I. Chứng minh rằng:
a) Các tam giác INE và INF là tam giác cân.
 Xem đáp án
Xem đáp án
a) Ta có: (góc nội tiếp chắn nửa đường tròn).
(tính chất tiếp tuyến).
(cùng phụ với ) (1)
Tam giác cân tại O nên (2)
Mà
(3)
Từ (1), (2) và (3) suy ra cân tại I .
Chứng minh hoàn toàn tương tự, ta cũng có: cân tại ![]() .
.