Dạng 4: Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại một góc bằng nhau
-
1091 lượt thi
-
11 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Trên các cạnh BC, BD của hình vuông ABCD ta lấy lần lượt các điểm M, N sao cho MAN = 45. Đường thẳng BD cắt các đường thẳng AM, AN tương ứng tại các điểm P, Q.
a) Chứng minh rằng các tứ giác ABMQ và ADNP nội tiếp.
Xem đáp án
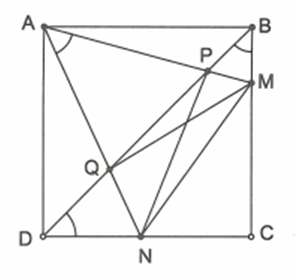
Các đỉnh A và B cùng nhìn đoạn thẳng MQ dưới một góc 45.
Vì vậy tứ giác ABMQ nội tiếp.
Tương tự ta suy ra tứ giác ADNP nội tiếp.
Câu 2:
b) Chứng minh rằng các điểm M, N, P, Q, C nằm trên cùng một đường tròn.
Xem đáp án
Do ABMQ là tứ giác nội tiếp nên AQM + ABM = 180 => AQM = 90.
Tương tự tứ giác ADNP nội tiếp suy ra APN = 90.
Tứ giác MNPQ là tứ giác nội tiếp vì có hai đỉnh Q và P cùng nhìn cạnh MN dưới một góc 90.
Suy ra bốn điểm M , Q , P cùng thuộc một đường tròn. (1)
Tứ giác MCNP là tứ giác nội tiếp vì MCN + MPN = 90 + 90 = 180.
Suy ra bốn điểm M , C , N , P cùng thuộc một đường tròn. (2)
Từ (1) và (2) suy ra các điểm M , N , P , Q , C cùng nằm trên một đường tròn.
Câu 3:
Cho hình vuông ABCD có hai đường chéo cắt nhau tại E. Lấy I thuộc cạnh AB, M thuộc cạnh BC sao cho IEM = 90 (I và M không trùng với các đỉnh của hình vuông).
a) Chứng minh rằng BIEM là tứ giác nội tiếp.
Xem đáp án
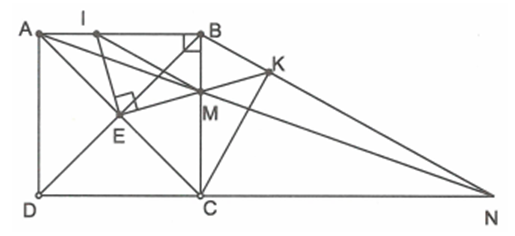
Theo giả thiết có:
IBM = IEM = 90 => IBM + IEM = 180.
Vậy tứ giác BIEM nội tiếp đường tròn đường kính IM.
Câu 4:
b) Tính số đo của góc IME.
Xem đáp án
Tứ giác BIEM nội tiếp suy ra:
IME = IBE = 45 (hai đỉnh cùng nhìn cạnh IE và ABCD là hình vuông).
Câu 5:
c) Gọi N là giao điểm của tia AM và tia DC; K là giao điểm của BN và tia EM. Chứng minh BKCE là tứ giác nội tiếp.
Xem đáp án
Xét EBI và ECM có: IBE = MCE = 45 (do ABCD là hình vuông);
BE = CE (do ABCD là hình vuông);
BEI = CEM (do cùng phụ với BEM).
=> EBI = ECM => MC = IB (hai cạnh tương ứng) => MB = IA.
Vì CN // BA nên theo định lí Ta-lét, ta có: . Suy ra IM // BN (định lí Ta-lét đảo).
=> IKE = IME. Lại có BCE = 45 (do ABCD là hình vuông).
Suy ra BKE = BCE. Tứ giác BKCE có hai đỉnh K và C kề nhau và cùng nhìn cạnh BE dưới một góc bằng nhau nên BKCE là tứ giác nội tiếp.
Câu 6:
Cho đường tròn đường kính AB, các điểm C , D nằm trên đường tròn đó sao cho C , D nằm khác phía đối với đường thẳng AB, đồng thời AD > AC. Gọi điểm chính giữa của các cung nhỏ AC, AD lần lượt là M , N; giao điểm của MD với CN là K; giao điểm của MN và AC, AD lần lượt là H , I.
a) Chứng minh ACN = DMN. Từ đó suy ra tứ giác MCKH.
Xem đáp án
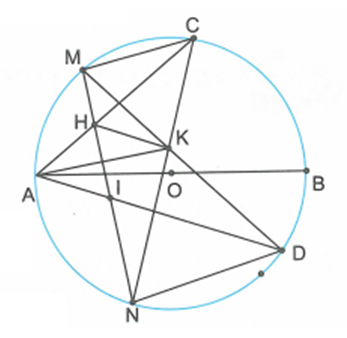
Vì N là điểm chính giữa của cung AD => AN = DN.
=> ACN = DMN (hai góc nội tiếp chắn hai cung bằng nhau AN, DN).
Khi đó tứ giác CMHK có hai đỉnh M và C cùng nhìn cạnh HK dưới một góc bằng nhau nên CMHK là tứ giác nội tiếp.
Câu 7:
b) Chứng minh KH song song với AD.
Xem đáp án
Theo câu a) có CMHK là tứ giác nội tiếp nên
CHK = CMK (cùng chắn cung CK). (1)
Xét đường tròn đường kính AB có
CMK = CAD (cùng chắn CD) (2)
Từ (1) và (2) suy ra CHK = CAD. Mà hai góc này ở vị trí đồng vị, suy ra HK // AD (đpcm).
Câu 8:
c) Tìm hệ thức liên hệ giữa sđ AC và sđ AD để AK song song với ND.
Xem đáp án
AK // ND <=> KAD = ADN = KMI => MAIK là tứ giác nội tiếp.
ADN = ACN = AMI = AKI => KAI = AKI => AKI cân tại I.
Mà IM là phân giác của góc AIK => MI AK.
Lại có AK // ND => MI ND hay MN ND => MND = 90 .
MD là đường kính của đường tròn đường kính AB.
=> MAD = 180 <=> sđ MA + sđ AD = 180 <=> sđ + sđ AD = 180.
Câu 9:
Cho đường tròn ( O ; R) và dây BC cố định, A là điểm di động trên cung lớn BC (A khác B, C) sao cho tam giác ABC nhọn. Các đường cao BD và CE của tam giác ABC cắt nhau tại điểm H. Kẻ đường kính AF của đường tròn ( O ), AF cắt BC tại điểm N.
a) Chứng minh tứ giác BEDC là tứ giác nội tiếp.
Xem đáp án
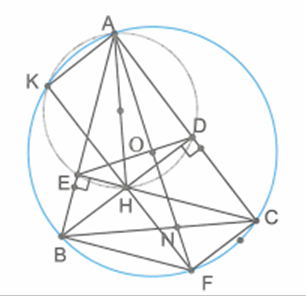
Tứ giác BEDC có BEC = BDC = 90 (giả thiết). Suy ra tứ giác BEDC là tứ giác nội tiếp (hai góc kề cùng nhìn cạnh BC dưới một góc bằng nhau).
Câu 10:
b) Chứng minh AE.AD = AD.AC
Xem đáp án
Tứ giác BEDC nội tiếp suy ra AED = ACB (góc ngoài của tứ giác nội tiếp).
Xét AED và ACB có: AED = ACB (chứng minh trên);
và BAC chung
=> AED đồng dạng ACB (g.g) => (hai cạnh tương ứng)
=> AE.AD = AD.AC.
Câu 11:
c) Chứng minh tứ giác BHCF là hình bình hành.
Xem đáp án
Ta có: BD // CF (vì cùng vuông góc với AC).
BF // EC (vì cùng vuông góc với AB).
Do đó BHCF là hình bình hành.
d) Ta thấy tứ giác ADHE nội tiếp đường tròn đường kính AH => AKH = 90 (1)
Mà AKF nội tiếp đường tròn đường kính AF => AKF = 90 (2)
Từ (1) và (2) suy ra ba điểm K , H , F thẳng hàng.