Dạng 3: Tứ giác có bốn đỉnh cách đều một điểm có đáp án
-
1090 lượt thi
-
4 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho hình thang ABCD ( AB // CD, AB < CD ) có C = D = 60, CD = 2AB. Chứng minh bốn điểm A, B, C, D cùng thuộc một đường tròn.
Xem đáp án
Gọi I là trung điểm CD, ta có: IC = AB và IC // AB => ICBA là hình bình hành.
=> BC = AI. (1)
Tương tự ABID là hình bình hành nên AD = BI. (2)
ABCD là hình thang có C = D = 60 nên ABCD là hình thang cân (3).
Từ (1), (2) và (3) ta có hai tam giác IAD = IBC đều hay IA = IB = IC = ID hay bốn điểm A, B ,C, D cùng thuộc một đường tròn.
Câu 2:
Cho nửa đường tròn tâm O đường kính AB = 2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (O) ( C là tiếp điểm). AC cắt OM tại E; MB cắt nửa đường tròn (O) tại D (D khác B). Chứng minh AMCO và AMDE là các tứ giác nội tiếp đường tròn.
Xem đáp án
Vì MA, MC là tiếp tuyến nên: MAO = MCO = 90
=> AMCO là tứ giác nội tiếp đường tròn đường kính MO.
ADB = 90 (góc nội tiếp chắn nửa đường tròn).
=> ADM = 90. (1)
Ta có OA = OC = R, MA = MC (tính chất tiếp tuyến).
Suy ra OM là đường trung trực của AC.
=> AEM = 90. (2)
Từ (1) và (2) suy ra AMDE là tứ giác nội tiếp đường tròn đường kính MA.
Câu 3:
Cho đường tròn tâm O. Kẻ đường kính AB và CD vuông góc với nhau. Gọi E là điểm chính giữa của cung nhỏ CB. EA cắt CD tại F, ED cắt AB tại M.
a) Các tam giác CEF và EMB là những tam giác gì?
Xem đáp án
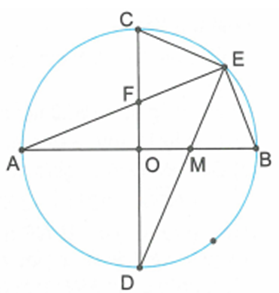
Ta thấy CFE là góc có đỉnh nằm bên trong đường tròn và chắn hai cung CE, AD.
FCE là góc nội tiếp chắn cung ED. Mà CE = EB, AD = BD nên FCE = CFE => CFE cân tại E.
Câu 4:
b) Chứng minh rằng bốn điểm C, F, M, B thuộc đường tròn tâm E.
Xem đáp án
Theo câu a), ECF và EBM là hai tam giác cân nên CE = EF, EM = EB.
Lại có CE = EB => CE = EB. Do đó CE = EF = EM = EB.
Vậy bốn điểm F, C, M, B thuộc đường tròn tâm E .