Trắc nghiệm Đường kính và dây của đường tròn có đáp án (Thông hiểu)
-
2008 lượt thi
-
5 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
Cho đường tròn (O) có bán kính R = 5cm. Khoảng cách từ tâm đến dây AB là 3cm. Tính độ dài dây AB.
Xem đáp án
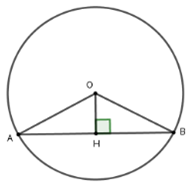
Kẻ OHAB tại H suy ra H là trung điểm AB
Xét tam giác OHB vuông tại H có OH = 3cm; OB = 5cm. Theo định lý Pytago ta có: HB = = 4
Mà H là trung điểm của AB nên AB = 2HB = 8cm
Vậy AB = 8cm
Đáp án cần chọn là: B
Câu 2:
Cho đường tròn (O) có bán kính R = 6,5cm. Khoảng cách từ tâm đến dây AB là 2,5cm. Tính độ dài dây AB
Xem đáp án
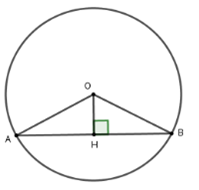
Kẻ OHAB tại H suy ra H là trung điểm AB
Xét tam giác OHB vuông tại H có OH = 2,5cm; OB = 6,5cm. Theo định lý Pytago ta có: HB = = 6
Mà H là trung điểm của AB nên AB = 2HB = 12cm
Vậy AB = 12cm
Đáp án cần chọn là: D
Câu 3:
Cho đường thẳng d cắt đường tròn (O) tại hai điểm phân biệt A, B. Biết khoảng cách từ điểm O đến đường thẳng d bằng 3cm và độ dài đoạn thẳng AB bằng 8cm. Bán kính của đường tròn (O) bằng:
Xem đáp án
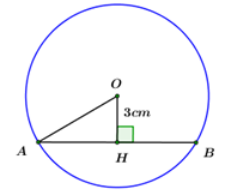
Kẻ OHAB. Khi đó H là trung điểm của AB (mối liên hệ giữa đường kính và dây cung)
Áp dụng định lý Pytago cho AOH vuông tại H ta có:
OA2 = AH2 + HO2 = 42 + 32 = 25 R = OA = 5cm
Đáp án cần chọn là: D
Câu 4:
Cho đường tròn (O), dây cùng AB và CD với CD < AB. Giao điểm K của các đường thẳng AB và CD nằm ngoài đường tròn. Vẽ đường tròn (O; OK), đường tròn này cắt KA và KC lần lượt tại M và N. So sánh KM và KN.
Xem đáp án
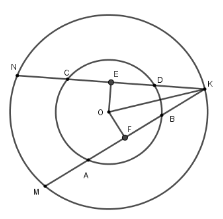
Xét đường tròn (O; OB)
Kẻ OECD; OFAB tại E; F mà CD < AB OE > OF (dây nào lớn hơn thì gần tâm hơn)
Xét đường trong (O; OK) có OEKN; OFKM tại El F mà OE > OF
KN < KM (liên hệ giữa dây và khoảng cách từ tâm đến dây)
Đáp án cần chọn là: B
Câu 5:
Cho đường tròn (O), dây cùng AB và CD với CD = AB. Giao điểm K của các đường thẳng AB và CD nằm ngoài đường tròn. Vẽ đường tròn (O; OK), đường tròn này cắt KA và KC lần lượt tại M và N. So sánh KM và KN.
Xem đáp án
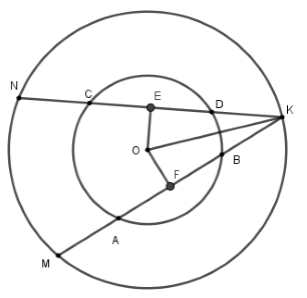
Xét đường tròn (O; OB)
Kẻ OECD; OFAB tại E; F mà CD = AB OE = OF (dây nào lớn hơn thì gần tâm hơn)
Xét đường trong (O; OK) có OEKN; OFKM tại El F mà OE = OF
KN = KM (liên hệ giữa dây và khoảng cách từ tâm đến dây)
Đáp án cần chọn là: C