10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán hình 9 ôn tập chương II có đáp án (Thông hiểu)

Trắc nghiệm Toán hình 9 ôn tập chương II có đáp án

Trắc nghiệm Toán hình 9 ôn tập chương II có đáp án (Thông hiểu)

2388 lượt thi
10 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

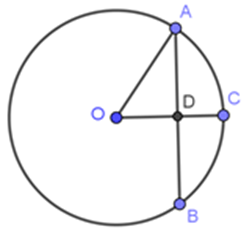
Trong hình vẽ bên cho OC $⊥$ AB, AB = 12cm, OA = 10cm. Độ dài AC là:

A. 8cm

B. 2 $\sqrt{10}$ cm

C. 4 $\sqrt{7}$ cm

D. 2cm

Xem đáp án

Vì OC vuông góc với AB nên D là trung điểm của AB (mối quan hệ giữa đường kính và dây) AD = $\frac{A B}{2} = \frac{12}{2}$ = 6cm

Xét tam giác AOD vuông tại D nên OD² = OA² – AD² = 10² – 6² = 64

OD = 8cm

Có OD + DC = OC nên DC = OC – OD = 10 – 8 = 2cm

Xét tam giác ADC vuông tại D nên AC² = AD² + DC² = 6² + 2² = 40

Vậy AC = 2 $\sqrt{10}$ cm

Đáp án cần chọn là: B

Câu 2:

Cho hai đường tròn (O; 4cm) và (O’; 3cm) biết OO’ = 5cm. Hai đường tròn cắt nhau tại A và B. Độ dài AB là:

A. 2,4cm

B. 4,8cm

C. $\frac{5}{12}$ cm

D. 5cm

Xem đáp án

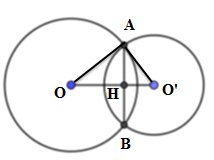
Xét tam giác OAO’ có OA² + O’A² = OO’² (vì 4² + 3² = 5²) nên tam giác OAO’ vuông tại A

Xét tam giác OAO’ có AH là đường cao nên AH.OO’ = OA.OA’

AH = $\frac{O A . O' A}{O O'} = \frac{4.3}{5} = \frac{12}{5}$

Mà AB = 2AH nên AB = $\frac{24}{5}$ = 4,8cm

Đáp án cần chọn là: B

Câu 3:

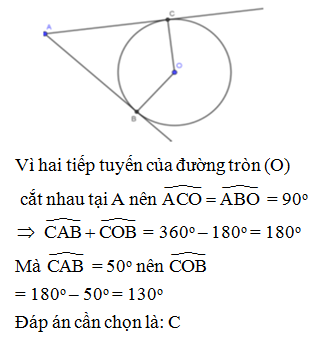
Hai tiếp tuyến tại A và B của đường tròn (O; R) cắt nhau tại M. Nếu MA = R $\sqrt{3}$ thì góc $\hat{A O B}$ bằng:

A. 120^o

B. 90^o

C. 60^o

D. 45^o

Xem đáp án

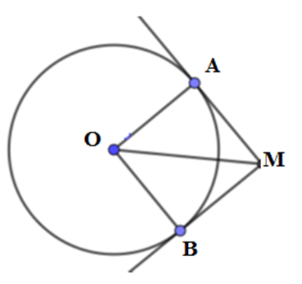
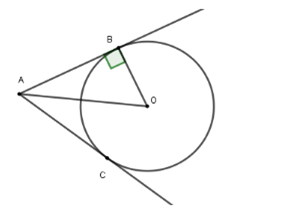
Có AM là tiếp tuyến của đường tròn (O) nên AM vuông góc với OA

Xét tam giác AOM vuông tại A nên có tan = $\hat{A O M}$ = $\frac{A M}{O A} = \frac{R \sqrt{3}}{R} = \sqrt{3}$

$\hat{A O M}$ = 60^o

Mà hai tiếp tuyến AM và BM cắt nhau tại M nên ta có OM là phân giác của $\hat{A O B}$

Vậy $\hat{A O B}$ = 2 $\hat{A O M}$ = 2.60^o = 120^o

Đáp án cần chọn là: A

Câu 4:

Cho hai đường tròn (O; 5) và (O’; 5) cắt nhau tại A và B. Biết OO’ = 8. Độ dài dây cung AB là

A. 6cm

B. 7cm

C. 5cm

D. 8cm

Xem đáp án

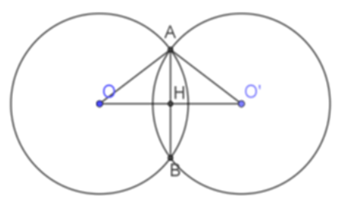
Ta có OA = O’A = 5cm nên tam giác AOO’ cân tại A.

Mà AH vuông góc với OO’ nên H là trung điểm của OO’. Suy ra OH = 4cm

Xét tam giác AOH vuông tại H nên suy ra

AH² = OA² – OH² = 5² – 4² = 9 = 3²

Vậy AH = 3cm

Mà AB = 2AH (mối quan hệ giữa đường nối tâm và dây cung)

Vậy AB = 6cm

Đáp án cần chọn là: A

Câu 5:

Cho đường tròn (O; 25cm) và dây AB bằng 40cm. Khi đó khoảng cách từ tâm O đến dây AB là:

A. 15cm

B. 7cm

C. 20cm

D. 24cm

Xem đáp án

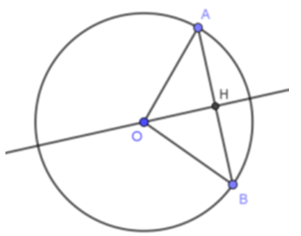
Từ O kẻ OH vuông góc với AB

Vậy H là trung điểm của AB (mối quan hệ giữa đường kính và dây)

suy ra AH = $\frac{A B}{2}$ = 20cm

Xét tam giác OAH vuông tại H nên theo định lý Pytago ta có:

OH² = OA² – AH² = 25² – 20² = 225 = 15²

Vậy OH = 15cm

Đáp án cần chọn là: A

Câu 6:

Cho tam giác ABC có AB = 5, AC = 12, BC = 13. Khi đó :

A. AB là tiếp tuyến của đường tròn (C; 5)

B. AC là tiếp tuyến của đường tròn (B; 5)

C. AB là tiếp tuyến của đường tròn (B; 12)

D. AC là tiếp tuyến của đường tròn (C; 13)

Xem đáp án

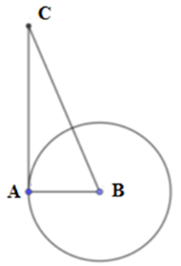
Xét $∆$ ABC có:

AB² + AC² = 5² + 12² = 169 = 13² = BC²

Áp dụng định lý Pytago đảo ta có ABC vuông tại A. Do đó AB AC

AB là tiếp tuyến của đường tròn (C; 12)

AC là tiếp tuyến của đường tròn (B; 5)

Đáp án cần chọn là: B

Câu 7:

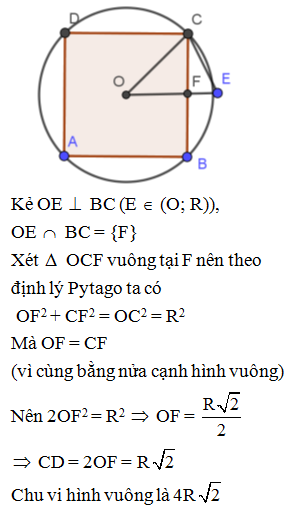
Cho hình vuông nội tiếp đường tròn (O; R). Chu vi của hình vuông là:

A. 2R $\sqrt{2}$

B. 3R $\sqrt{2}$

C. 4R $\sqrt{2}$

D. 6R

Xem đáp án

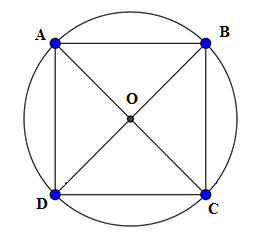
Hình vuông ABCD nội tiếp đường tròn tâm O

Khi đó đường chéo BD là đường kính của (O)

Suy ra BD = 2R

Xét tam giác BDC vuông cân tại C, theo định lý Pytago ta có:

BC² + CD² = BD² 2BC² = 4R² BC = R $\sqrt{2}$

Chu vi hình vuông ABCD là 4 R $\sqrt{2}$

Đáp án cần chọn là: C

Chú ý

Câu 8:

Hai tiếp tuyến tại hai điểm B, C của một đường tròn (O) cắt nhau tại A tạo thành $\hat{B A C}$ = 50^o. Số đo của góc $\hat{B O C}$ bằng:

A. 30^o

B. 40^o

C. 130^o

D. 310^o

Xem đáp án

Câu 9:

Cho hình vẽ dưới đây. Biết $\hat{B A C}$ = 60^o; AO = 10cm. Chọn đáp án đúng.

Độ dài bán kính OB là:

A. 4 $\sqrt{3}$

B. 5

C. 5 $\sqrt{3}$

D. 10 $\sqrt{3}$

Xem đáp án

Câu 10:

Cho tam giác ABC nhọn và có các đường cao BD, CE. So sánh BC và DE

A. BC = DE

B. BC < DE

C. BC > DE

D. BC = $\frac{2}{3}$ DE

Xem đáp án

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán hình 9 ôn tập chương II có đáp án

Trắc nghiệm Toán hình 9 ôn tập chương II có đáp án (Thông hiểu)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương