15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán hình 9 ôn tập chương II có đáp án

Câu 1:

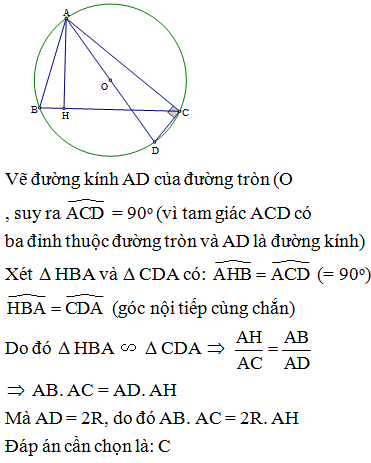
Cho đường tròn (O; R), đường kính AB cố định và dây AC. Biết rằng khoảng cách từ O lần lượt đến AC và BC là 8cm và 6cm. Lấy D đối xứng với A qua C. Chọn câu sai?

A. AC = 12cm; BC = 16cm

B. Khi C di chuyển trên đường tròn (O) thì điểm D thuộc đường tròn cố định tâm B và bán kính bằng 2R

C. $∆$ ABD cân tại B

D. Khi C di chuyển trên đường tròn (O) thì điểm D thuộc đường tròn cố định tâm B và bán kính bằng $\frac{3}{2}$ R

Xem đáp án

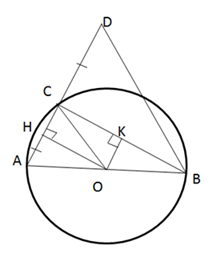
Kẻ OH, OK lần lượt vuông góc với AC và BC, ta có:

OH = 8 (cm); OK = 6 (cm) và HA = HC = $\frac{A C}{2}$ ; KB = KC = $\frac{BC}{2}$ (định lí đường kính dây cung)

AB là đường kính nên $\hat{A C B}$ = 90^o

Do đó tứ giác CHOK là hình chữ nhật (có ba góc vuông)

OH = CK = 8 (cm) BC = 16 (cm)

Tương tự ta có AC = 12 (cm)

Xét tam giác vuông OHC, ta có:

OC = $\sqrt{O H^{2} + H C^{2}} = \sqrt{8^{2} + 6^{2}}$ = q0 (cm) (Định lý Pytago)

$∆$ ABD có đường cao BC đồng thời là đường trung tuyến nên ABD cân tại B

Ta có BD = BA = 2R (cm), điểm B cố định, 2R không đổi.

Vậy D thuộc đường tròn cố định tâm B và bán kính bằng 2R. Do đó D sai

Đáp án cần chọn là: D

Câu 2:

Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax và By (Ax và By và nửa đường tròn cùng thuộc về một nửa mặt phẳng bờ là AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax và By theo thứ tự tại C và D. Tìm vị trí điểm M để tứ giác ABDC có chu vi nhỏ nhất.

A. M là trung điểm của CD

B. OM // AB

C. OM $⊥$ AB

D. OM // Ax

Xem đáp án

Câu 3:

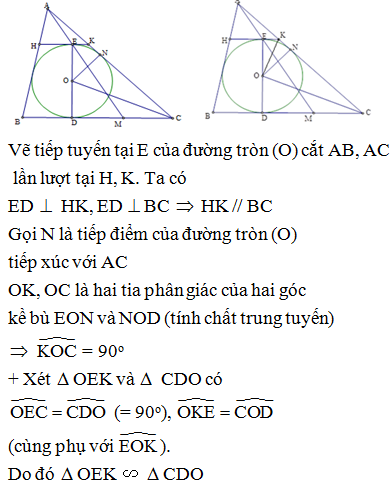
Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax và By (Ax và By và nửa đường tròn cùng thuộc về một nửa mặt phẳng bờ là AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax và By theo thứ tự tại C và D. Tìm vị trí điểm C và D để hình thang ABDC có chu vi bằng 14, biết AB = 4cm

A. AC = 4cm; BD = 1cm hoặc AC = 1cm; BD = 4cm

B. AC = 4cm; BD = 1cm

C. AC = 3cm; BD = 2cm hoặc AC = 2cm; BD = 3cm

D. AC = 3cm; BD = 1cm hoặc AC = 1cm; BD = 3cm

Xem đáp án

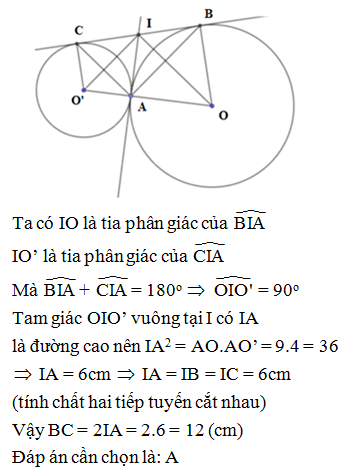
Theo tính chất hai tiếp tuyến cắt nhau: AC = CM và BD = DM

Xét tứ giác ABDC có: AC // BD ABDC là hình thang

IO là đường trung bình của hình thang ABDC

IO // AC // BD mà AC $⊥$ AB => IO $⊥$ AB (1)

IO = $\frac{A C + B D}{2} = \frac{C M + D M}{2} = \frac{C D}{2}$ (2)

Suy ra tam giác COD vuông tại O

C_ABDC = 14 => AB + 2CD = 14 =>CD = $\frac{14 - A B}{2} = \frac{14 - 4}{2}$ = 5cm

Lại có: CD = CM + DM = AC + BD AC = CD – BD = 5 – BD

Mà tam giác COD vuông tại O

Áp dụng hệ thức lượng vào tam giác vuông COD ta có:

OM² = CM . DM 2² = AC . BD AC . BD = 4 (5 – BD). BD = 4

5BD – BD² = 4 BD² – 5BD + 4 = 0 BD² – BD – 4BD + 4 = 0

BD (BD – 1) – 4(BD – 1) = 0 (BD – 1) (BD – 4) = 0

$\Leftrightarrow [\begin{array}{l} B D - 1 = 0 \\ B D - 4 = 0 \end{array} \Leftrightarrow [\begin{array}{l} B D = 1 \Rightarrow A C = 4 \\ B D = 4 \Rightarrow A C = 1 \end{array}$

Vậy với AC = 4cm; BD = 1cm hoặc AC = 1cm; BD = 4cm thì chu vi của hình thang ABDC bằng 14

Đáp án cần chọn là: A

Câu 4:

Cho nửa đường tròn (O) có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn cùng thuộc về một nửa mặt phẳng bờ là AB). Qua một điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt Ax và By theo thứ tự ở C và D. Gọi N = AD BC, H = MN AB. Chọn câu đúng nhất.

A. MN $⊥$ AB

B. MN > NH

C. Cả A, B đều đúng

D. Cả A, B đều sai

Xem đáp án

Câu 5:

Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B $\in$ (O) và C $\in$ (O’). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC tại I. Tính độ dài BC biết OA = 9cm, O’A = 4cm

A. 12 cm

B. 18cm

C. 10cm

D. 6cm

Xem đáp án

Câu 6:

Cho tam giác ABC nội tiếp đường tròn (O; R) có AB = 5cm, AC = 12cm và đường cao AH = 3cm (H nằm ngoài BC), khi đó R bằng?

A. 6cm

B. 6,5cm

C. 5cm

D. 7,5cm

Xem đáp án

Câu 7:

Tam giác đều có cạnh 8cm thì bán kính đường tròn nội tiếp tam giác là?

A. 2 $\sqrt{3}$ cm

B. 4 $\sqrt{3}$ cm

C. $\frac{2 \sqrt{3}}{3}$ cm

D. $\frac{4 \sqrt{3}}{3}$ cm

Xem đáp án

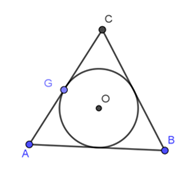
Gọi O là tâm đường tròn nội tiếp tam giác đều ABC. Vậy O là giao điểm 3 đường phân giác của tam giác mà tam giác ABC đều nên O là giao điểm 3 đường trung tuyến của tam giác ABC. Vậy bán kính đường tròn (O) là OG với BG là trung tuyến của tam giác ABC

Vì tam giác ABC đều nên ta tính được:

BG = $\sqrt{B C^{2} - C G^{2}} = \sqrt{8^{2} - 4^{2}} = 4 \sqrt{3}$ cm => OG = $\frac{B G}{3} = \frac{4 \sqrt{3}}{3}$ cm

Đáp án cần chọn là: D

Câu 8:

Hai tiếp tuyến tại A và B của đường tròn (O; R) cắt nhau tại M. Nếu MA = R thì góc ở tâm $\hat{A O B}$ bằng:

A. 120^o

B. 90^o

C. 60^o

D. 45^o

Xem đáp án

Câu 9:

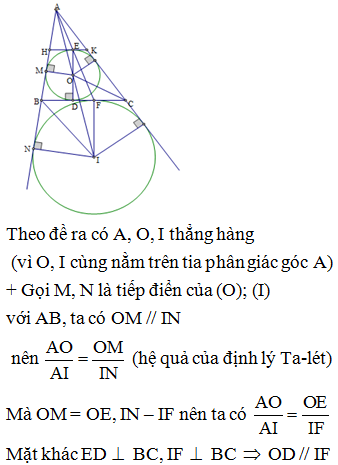
Cho đường tròn (O; R), AC và BD là hai đường kính. Xác định vị trí của hai đường kính AC và BD để diện tích tứ giác ABCD lớn nhất

A. AC $⊥$ BD

B. AC tạo với BD góc 45^o.

C. AC tạo với BD góc 30^o.

D. AC tạo với BD góc 60^o.

Xem đáp án

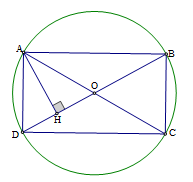
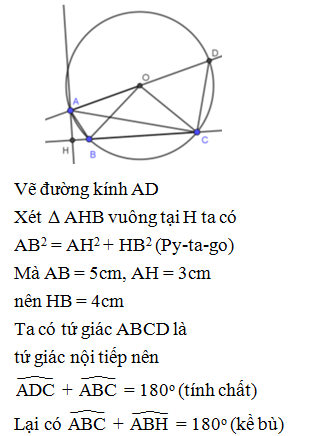
Vẽ AH $⊥$ BD (H $\in$ BD)

Tứ giác ABCD có OA = OC = R, OB = OD = R nên là hình bình hành

Mà AC = BD = 2R do đó tứ giác ABCD là hình chữ nhật, suy ra S_ABCD = AB.AD

$∆$ ABD có $\hat{A}$ = 90^o, AH $⊥ DB$ nên AB.AD = AH.DB

Vì AH AO, DB = 2R nên S_ABCD 2R² (không đổi).

Dấu “=” xảy ra H $\equiv$ O => AC $⊥$ BD

Vậy khi hai đường kính AC và BD vuông góc với nhau thì diện tích tứ giác ABCD lớn nhất.

Đáp án cần chọn là: A

Câu 10:

Cho đường tròn (O; R) đường kính AB. CD là dây cung của (O), $\hat{C O D}$ = 90^o, CD cắt AB tại M (D nằm giữa C và M) và OM = 2R. Tính độ dài các đoạn thẳng MD, MC theo R.

A. MC = $\frac{R \sqrt{2}}{2} (\sqrt{5} + 1)$ ; MD = $\frac{R \sqrt{2}}{2} (\sqrt{5} - 1)$

B. MC = $\frac{R \sqrt{3}}{2} (\sqrt{7} + 1)$ ; MD = $\frac{R \sqrt{3}}{2} (\sqrt{7} - 1)$

C. MC = $\frac{R}{2} (\sqrt{7} + 1)$ ; MD = $\frac{R}{2} (\sqrt{7} - 1)$

D. MC = $\frac{R \sqrt{2}}{2} (\sqrt{7} + 1)$ ; MD = $\frac{R \sqrt{2}}{2} (\sqrt{7} - 1)$

Xem đáp án

Câu 11:

Cho đường tròn (O; r) nội tiếp tam giác ABC tiếp xúc với BC tại D. Vẽ đường kính DE; kéo dài AE cắt BC tại M. chọn câu đúng nhất.

A. BD > CM

B. BD < CM

C. BD = CM

D. Không đủ điều kiện so sánh

Xem đáp án

Câu 12:

Cho tam giác ABC. Một đường tròn tâm O nội tiếp tam giác ABC và tiếp xúc với BC D. Đường tròn tâm I là đường tròn bàng tiếp trong góc A của tam giác ABC và tiếp xúc với BC tại F. Vẽ đường kính DE của đường tròn (O). Chọn đáp án đúng nhất.

A. $\frac{A O}{A I} = \frac{O E}{I F}$

B. $\hat{AOE} = \hat{AIF}$

C. A, E, F thẳng hàng

D. Cả A, B, C đều đúng

Xem đáp án

Câu 13:

Đường tròn tâm I nội tiếp tam giác ABC tiếp xúc với BC, AB, AC lần lượt ở D, E, F. Đường thẳng qua E song song với BC cắt AD, DF lần lượt ở M, N. Khi đó M là trung điểm của đoạn thẳng

A. EN

B. AD

C. Cả A, B đều đúng

D. Cả A, B đều sai

Xem đáp án

Câu 14:

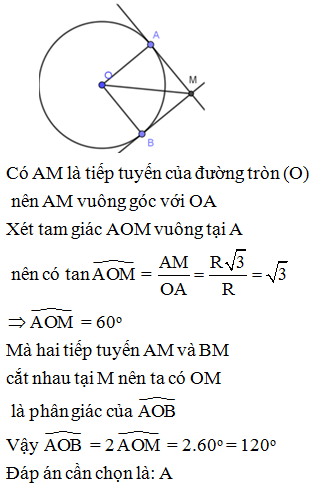
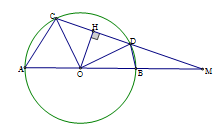
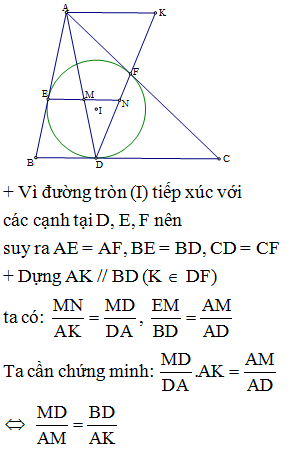
Cho tam giác nhọn ABC. Gọi O là trung điểm của BC. Dựng đường tròn tâm O đường kính BC. Vẽ đường cao AD của tam giác ABC và các tiếp tuyến AM, AN với đường tròn (O) (M, N là các tiếp điểm). Gọi E là giao điểm của MN với AD. Chọn câu đúng.

A. AE . AD = 2 . AM

B. AE . AD = AM²

C. AE . AO = AM²

D AD . AO = AM²

Xem đáp án

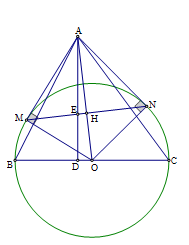
AM, AN là các tiếp tuyến của đường tròn (O), gọi H là giao điểm của AO và MN

Theo tính chất hai tiếp tuyến cắt nhau ta có: AM = AN; OM = ON nên AO là đường trung trực của đoạn MN

Suy ra AO $⊥$ MN

Ta có tam giác AHE đồng dạng với tam giác ADO (vì $\hat{AHE} = \hat{ADO}$ = 90^o; $\hat{DAO}$ chung) nên AE. AD = AH. AO (1)

Cũng theo hệ thức lượng trong tam giác vuông AMO ta có: AH. AO = AM². (2)

Từ (1) và (2) suy ra AE. AD = AM²

Đáp án cần chọn là: B

Câu 15:

Cho tam giác ABC nội tiếp đường tròn (O; R), AH là đường cao (H BC). Chọn câu đúng.

A. AB. AC = R. AH

B. AB. AC = 3R. AH

C. AB. AC = 2R. AH

D. AB. AC = R². AH

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán hình 9 ôn tập chương II có đáp án

Trắc nghiệm Toán hình 9 ôn tập chương II có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương