Dạng 4. Giải bài toán hệ thức lượng bằng phương pháp đại số
-
1232 lượt thi
-
6 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC vuông ở A, đương cao AH. Biết AB = 20cm, HC = 9cm. Tính độ dài AH.
 Xem đáp án
Xem đáp án
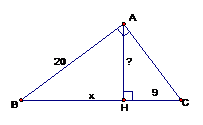
Đặt . Áp dụng hệ thức lượng trong tam giác ABC vuông ở A, có đường cao AH. Ta được: hay
Thu gọn ta được phương trình :
Giải phương trình này ta được ; (loại)
Dùng định lý Pitago tính được AH = 12 cm
Lưu ý : Giải PT bậc 2 nên dùng máy tính để giải cho nhanh.
Thuộc một số bộ ba số Pitago càng tốt để mau chóng ghi kết quả
Câu 2:
Cho tam giác ABC , , BC = 8cm; AB + AC = 12cm . Tính độ dài cạnh AB.
 Xem đáp án
Xem đáp án
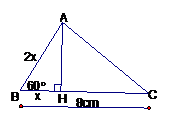
Kẻ AH BC. Đặt . Từ đó tính được và ;
Áp dụng định lí Pitago ta cho tam giác AHC vuông tại H
Ta có: AC =
Do AB + AC = 12 nên
Giải PT trên ta được : x = 2,5
AB = 2.2,5 = 5cm
Chú ý: Ta cũng tính được chu vi tam giác ABC = 20cm .
Diện tích tam giác ABC = cm.
Câu 3:
Cho tam giác ABC vuông tại A có BD là phân giác. Biết rằng AD = 1cm; BD = cm. Tính độ dài cạnh BC (nhập kết quả dưới dạng số thập phân)
 Xem đáp án
Xem đáp án
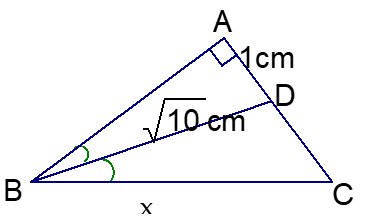
Áp dụng định lí Pitago tính được AB = 3cm.
Đặt BC = x , dùng Pitago tính được .
Do AD = 1 nên DC = – 1
Tam giác ABC có BD là phân giác góc ABC nên :
hay . Từ đó ta được phương trình
Giải phương trình tìm được x = 3,75cm
Trả lời : BC = 3,75cm
Câu 4:
Cho hình thang cân ABCD, đáy lớn CD = 10cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên . Tính độ dài đường cao của hình thang cân đó.
 Xem đáp án
Xem đáp án
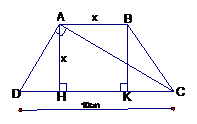
Kẻ AH CD ; BK CD. Đặt AH = AB = x HK = x
(cạnh huyền- góc nhọn)
Suy ra : .
Vậy
Áp dụng hệ thức lượng cho tam giác ADC vuông ở A có đường cao AH
Ta có : hay
Giải phương trình trên ta được và (loại)
Vậy :
Câu 5:
Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6cm, đường cao ứng với cạnh bên dài 12cm. Tính độ dài cạnh đáy BC.
 Xem đáp án
Xem đáp án
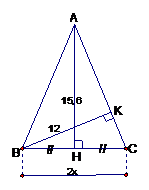
Đặt , từ tính chất của tam giác cân ta suy ra
Áp dụng định lí Pitago tính được
Từ hai tam giác vuông KBC và HAC đồng dạng ta được:
hay
Đưa về phương trình
Giải phương trình trên ta được nghiệm dương x = 6,5
Vậy (cm)
Câu 6:
Tính độ dài cạnh AB của tam giác ABC vuông tại A có hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm.
 Xem đáp án
Xem đáp án
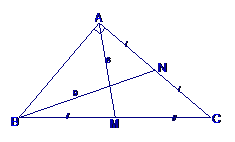
Đặt
Áp dụng tính chất đường trung tuyến trong tam giác vuông ứng với cạnh huyền ta được (cm)
Dùng định lí Pitago cho hai tam giác vuông ABC và ABN vuông tại A
Ta được:
và
Thay (2) vào (1) ta được phương trình :
Thu gọn phương trình trên ta được phương trình :
Nghiệm dương của phương trình :
Trả lời: cm
