14 câu hỏi trắc nghiệm thuộc Dạng 2. Tỉ số lượng giác của góc nhọn

Câu 1:

Cho tam giác vuông tại A, trong đó AC = 0,9m; AB = 1,2 m.Tính các tỉ số lượng giác của góc B, từ đó suy ra tỉ số lượng giác của góc C.

Xem đáp án

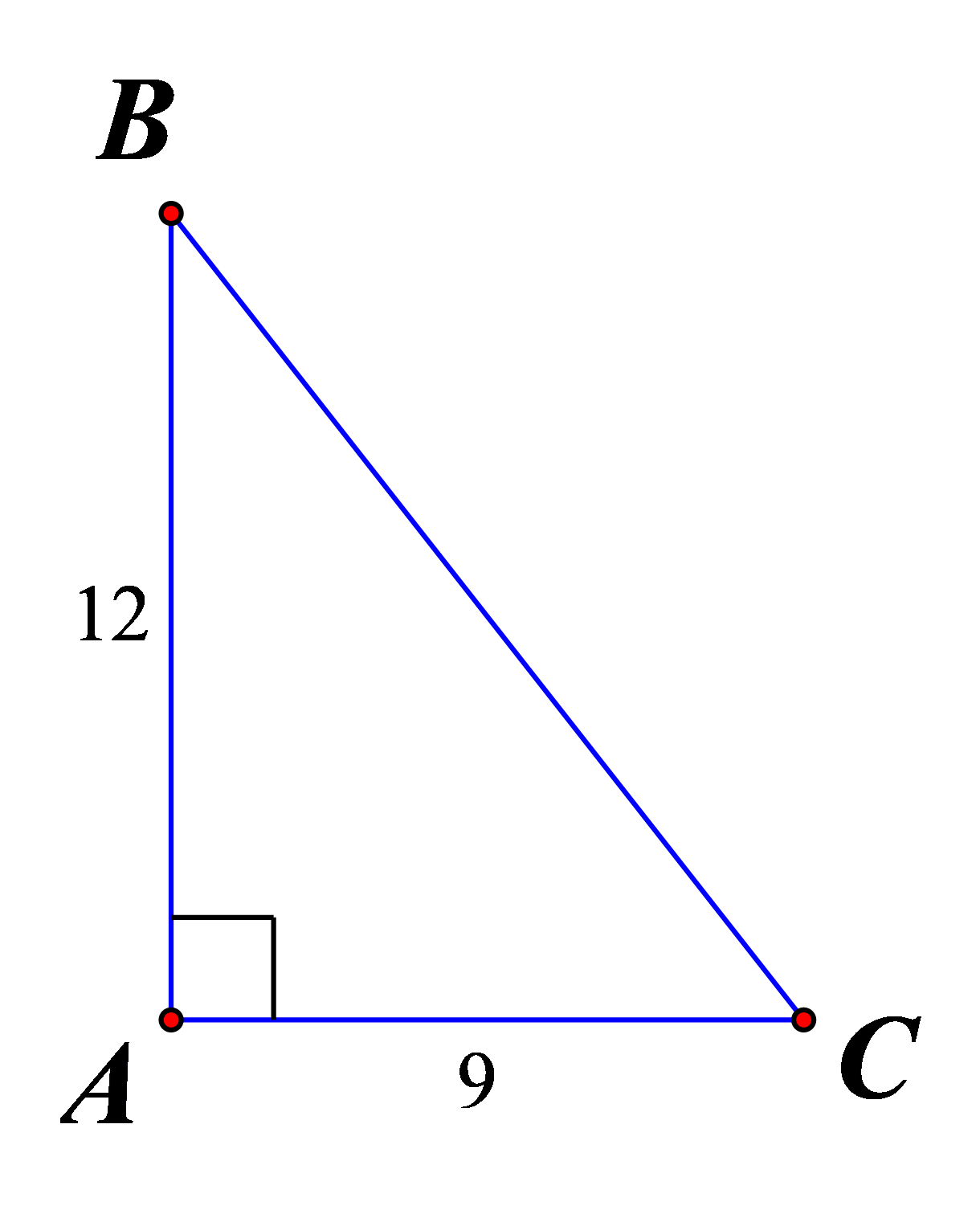
Ta có AC = 9 dm, AB = 12 dm.Theo định lí Pitago, ta có

$B C = \sqrt{A C^{2} + A B^{2}} = \sqrt{9^{2} + 12^{2}} = 15$ (dm)

Vậy $s i n B = \frac{A C}{B C} = \frac{9}{15} = \frac{3}{5}$

$C o s B = \frac{A B}{B C} = \frac{12}{15} = \frac{4}{5}; t a n B = \frac{A C}{A B} = \frac{9}{12} = \frac{3}{4}; c o t B = \frac{A B}{A C} = \frac{12}{9} = \frac{4}{3}$

Vì góc B và góc C là hai góc phụ nhau nên:

$S i n B = c o s C = \frac{3}{5}; C o s B = s i n C = \frac{4}{5}; t a n B = c o t C = \frac{3}{4}; c o t B = t a n C = \frac{4}{3}$

Câu 2:

Chứng minh các hệ thức:

$1 + \tan^{2} α = \frac{1}{\cos^{2} α}$

Xem đáp án

Ta có

1 + \tan^{2} α = 1 + {(\frac{\sin α}{\cos α})}^{2} = 1 + \frac{\sin^{2} α}{\cos^{2} α} = \frac{\cos^{2} α + \sin^{2} α}{\cos^{2} α} = \frac{1}{\cos^{2} α}

Câu 3:

Chứng minh các hệ thức:

1 + \cot^{2} α = \frac{1}{\sin^{2} α}

Xem đáp án

Ta có $1 + \cot^{2} α = 1 + {(\frac{\cos α}{\sin α})}^{2} = 1 + \frac{\cos^{2} α}{\sin^{2} α} = \frac{\sin^{2} α + \cos^{2} α}{\sin^{2} α} = \frac{1}{\sin^{2} α}$

Nhận xét: Trong cách giải trên ta đã biến đổi vế trái thành vế phải. Ta cũng có thể biến đổi vế phải thành vế trái theo chiều ngược lại.

Hai hệ thức trên cũng là hệ thức cơ bản, nên nhớ để sau này vận dụng.

Câu 4:

Cho $α$ là một góc nhọn. Chứng minh rằng:

$s i n α < t a n α$

Xem đáp án

Media VietJack

Ta có $\sin α = \frac{A C}{B C}; \tan α = \frac{A C}{A B}$ mà BC > AB nên $\frac{AC}{BC} < \frac{AC}{AB}$

Do đó $s i n α < t a n α;$

Câu 5:

Cho

α

là một góc nhọn. Chứng minh rằng:

c o s α < c o t α

Xem đáp án

Ta có $\cos α = \frac{A B}{B C}; \cot α = \frac{A B}{A C}$ mà BC > AC nên $\frac{A B}{B C} < \frac{A B}{A C}$

Do đó $c o s α < c o t α$

Nhận xét: Phương pháp giải ví dụ này là dùng định nghĩa của tỉ số lượng giác.

Câu 6:

Chứng minh định lí sin: Trong một tam giác nhọn, độ dài các cạnh tỉ lệ với sin của các góc đối diện:

\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}

Xem đáp án

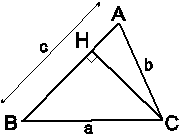
* Tìm cách giải:

Để có sin A (hoặc sin B, sin C) thì phải xét tam giác vuông với A là một góc nhọn. Do đó phải vẽ thêm đường cao.

* Trình bày lời giải:

Vẽ đường cao CH.

Xét DACH vuông tại H ta có: $\sin A = \frac{CH}{AC}$ (1)

Xét DBCH vuông tại H ta có: $\sin B = \frac{CH}{BC}$ (2)

Từ (1) và (2) suy ra $\frac{\sin A}{\sin B} = \frac{C H}{A C} : \frac{C H}{B C} = \frac{B C}{A C} = \frac{a}{b}$ . Do đó $\frac{a}{\sin A} = \frac{b}{\sin B}$

Chứng minh tương tự ta được $\frac{b}{\sin B} = \frac{c}{\sin C}$

Vậy $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Lưu ý: Nếu DABC có $\hat{C} \geq 90^{°}$ thì ta vẫn có: $\frac{a}{\sin A} = \frac{b}{\sin B}$

Câu 7:

Tìm góc x, biết rằng: $t a n x = 3 c o t x$

Xem đáp án

$t a n x = 3 c o t x;$ . Suy ra $\tan x = \frac{3}{\tan x}$ (vì $\cot x = \frac{1}{\tan x}$ ).

Do đó $t a n^{2} x = 3$ Þ $\tan x = \sqrt{3} = \tan 60^{°}$ Vậy $x = 60^{o} .$

Câu 8:

Tìm góc x, biết rằng:

\sin x + \cos x = \sqrt{2}

Xem đáp án

Bình phương hai vế ta được: $s i n^{2} x + 2 s i n x . c o s x + c o s^{2} x = 2$

Û $2 s i n x . c o s x + 1 = 2$ (vì $s i n^{2} x + c o s^{2} x = 1$ )

Û $2 s i n x . c o s x = 1$ Û $1 - 2 s i n x . c o s x = 0$ Û $s i n^{2} x - 2 s i n x . c o s x + c o s^{2} x = 0$

Û ${(s i n x - c o s x)}^{2} = 0$ . Do đó $s i n x = c o s x$

Û $s i n x = s i n (90^{o} - x)$ (vì $c o s x = s i n (90^{o} - x)$ )

Dẫn tới $x = 90^{o} - x \Leftrightarrow 2 x = 90^{o} \Leftrightarrow x = 45^{o} .$

Nhận xét: Phương pháp chung để giải ví dụ này là tìm cách đưa phương trình có hai tỉ số lượng giác về dạng còn một tỉ số lượng giác bằng cách vận dụng quan hệ giữa các tỉ số lượng giác đó

Câu 9:

Không dùng máy tính hoặc bảng số, tính giá trị của các biểu thức sau bằng cách hợp lí:

$P = \sin^{2} 1^{°} + \sin^{2} 2^{°} + \sin^{2} 3^{°} + \dots + \sin^{2} 88^{°} + \sin^{2} 89^{°}$

Xem đáp án

Áp dụng định lí nếu hai góc phụ nhau thì sin của góc này bằng côsin góc kia, tang của góc này bằng côtang góc kia, ta có:

$P = \sin^{2} 1^{°} + \sin^{2} 2^{°} + \sin^{2} 3^{°} + \dots + \sin^{2} 88^{°} + \sin^{2} 89^{°}$

$= (\sin^{2} 1^{°} + \sin^{2} 89^{°}) + (\sin^{2} 2^{°} + \sin^{2} 88^{°}) + .... + (\sin^{2} 44^{°} + \sin^{2} 46^{°}) + \sin^{2} 45^{°} = (\sin^{2} 1^{°} + c {os}^{2} 1^{°}) + (\sin^{2} 2^{°} + c {os}^{2} 2^{°}) + .... + (\sin^{2} 44^{°} + c {os}^{2} 44^{°}) + \sin^{2} 45^{°}$

= $1 + 1 + 1 + ... + 1 + {(\frac{\sqrt{2}}{2})}^{2} = 44, 5$

Câu 10:

Không dùng máy tính hoặc bảng số, tính giá trị của các biểu thức sau bằng cách hợp lí:

Q = \tan 15^{0} . \tan 25^{0} . \tan 35^{0} . \tan 45^{0} . \tan 55^{0} . \tan 65^{0} . \tan 75^{0}

Xem đáp án

Áp dụng định lí nếu hai góc phụ nhau thì sin của góc này bằng côsin góc kia, tang của góc này bằng côtang góc kia, ta có:

$Q = \tan 15^{0} . \tan 25^{0} . \tan 35^{0} . \tan 45^{0} . \tan 55^{0} . \tan 65^{0} . \tan 75^{0} = (\tan 15^{0} . \tan 75^{0}) . (\tan 25^{0} . \tan 65^{0}) . (\tan 35^{0} . \tan 55^{0}) . \tan 45^{0} = (\tan 15^{0} . c o t 15^{0}) . (\tan 25^{0} . c o t 65^{0}) . (\tan 35^{0} . c o t 35^{0}) . \tan 45^{0} = 1.1.1.1 = 1$

Câu 11:

Không dùng máy tính hoặc bảng số, tính giá trị của các biểu thức sau bằng cách hợp lí: Biết $\cos α = \frac{20}{29}$ Tính $s i n α, t a n α$ và $\cot α .$

Xem đáp án

Áp dụng định lí nếu hai góc phụ nhau thì sin của góc này bằng côsin góc kia, tang của góc này bằng côtang góc kia, ta có:

Ta có $s i n^{2} α + c o s^{2} α = 1 \Rightarrow \sin^{2} α = 1 - \cos^{2} α = 1 - {(\frac{20}{29})}^{2} = \frac{441}{841}$

Do đó $\sin α = \frac{21}{29}; \tan α = \frac{\sin α}{\cos α} = \frac{21}{29} : \frac{20}{29} = \frac{21}{20}; \cos α = \frac{20}{21}$

Câu 12:

Cho tam giác ABC vuông tại A, đường cao AH. Tính sin B, sin C biết rằng:

AB = 13 và BH = 5

Xem đáp án

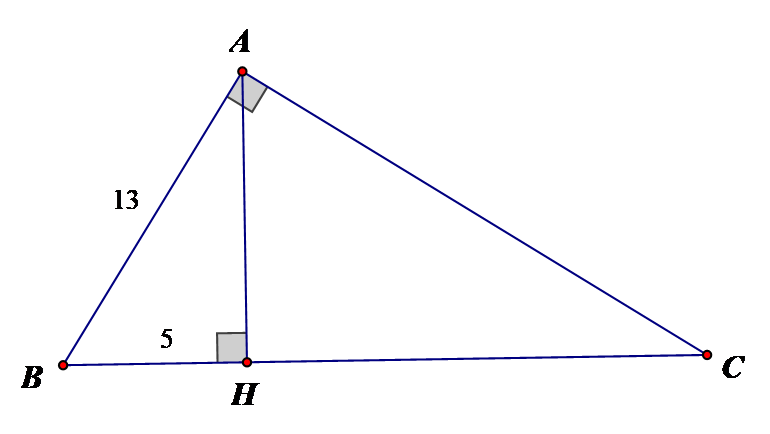
Tam giác ABC vuông tại A, đường cao AH ta có

$A B^{2} = B H . B C$ $\Rightarrow B C = \frac{A B^{2}}{B H} = \frac{13^{2}}{5} = 33, 8$

Áp dụng định lý Pytago trong tam giác vuông ABC ta có: $A C = \sqrt{B C^{2} - A B^{2}} = 31, 2$

$S i n B = \frac{A C}{B C} = \frac{31, 2}{33, 8} = \frac{12}{13} S i n C = \frac{A B}{B C} = \frac{13}{33, 8} = \frac{5}{13}$

Câu 13:

Cho tam giác ABC vuông tại A, đường cao AH. Tính sin B, sin C biết rằng:BH = 3 và CH = 4.

Xem đáp án

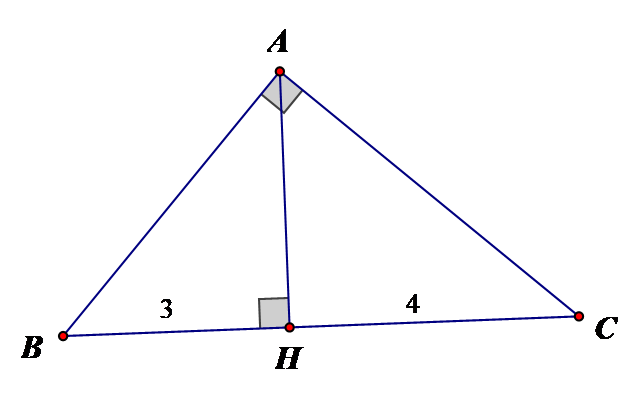
Tam giác ABC vuông tại A, đường cao AH ta có $A H^{2} = B H . C H = 3.4 \Rightarrow A H = 2 \sqrt{3}$

Tam giác ABH vuông. Theo định lý Pytago ta có

$A B = \sqrt{H B^{2} + A H^{2}} = \sqrt{3^{2} + 12} = \sqrt{21} S i n B = \frac{A H}{A B} = \frac{2 \sqrt{3}}{\sqrt{21}} = \frac{2}{\sqrt{7}}$

Tam giác ABC vuông, $B C = B H + H C = 3 + 4 = 7$

Theo định lý Pytago ta có $A C = \sqrt{B C^{2} - A B^{2}} = \sqrt{49 - 21} = \sqrt{28} = 2 \sqrt{7}$

$S i n C = \frac{A B}{B C} = \frac{\sqrt{21}}{7}$

Cách 2: Tam giác AHC vuông tại H; Theo định lý Pytago có

$A C = \sqrt{A H^{2} + H C^{2}} = \sqrt{12 + 16} = \sqrt{28} S i n C = \frac{A H}{A C} = \frac{\sqrt{12}}{\sqrt{28}} = \sqrt{\frac{3}{7}} = \frac{\sqrt{21}}{7}$

Nhận xét: Học sinh vận dụng các hệ thức giữa cạnh và đường cao trong tam giác vuông từ đó tính ra tỉ số lượng giác của các góc nhọn trong tam giác vuông.

Câu 14:

Cho tam giác ABC vuông tại A . Chứng minh rằng $\tan \frac{\hat{A B C}}{2} = \frac{A C}{A B + B C}$

Xem đáp án

Vẽ đường phân giác BD của $Δ$ ABC ( D $\in$ AC ).

Theo tính chất đường phân giác của tam giác ta có : $\frac{A D}{D C} = \frac{A B}{B C} \Leftrightarrow \frac{A D}{A B} = \frac{D C}{B C}$

$\Rightarrow \frac{A D}{A B} = \frac{A D + D C}{A B + B C} \Rightarrow \frac{A D}{A B} = \frac{A C}{A B + B C}$

Xét ABD có $\hat{B A D} = 90^{0} \Rightarrow \tan \hat{A B D} = \frac{A D}{A B}$

$\Leftrightarrow \tan \frac{\hat{A B C}}{2} = \frac{A C}{A B + B C}$

Vậy $\tan \frac{\hat{A B C}}{2} = \frac{A C}{A B + B C}$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập Toán 9 Chủ đề 1: Hệ thức lượng trong tam giác vuông có đáp án

Dạng 2. Tỉ số lượng giác của góc nhọn

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương