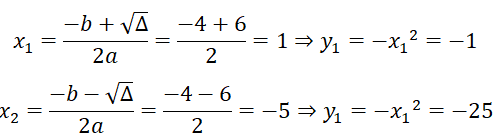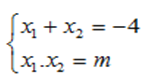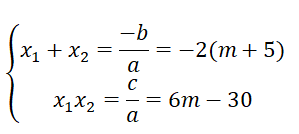Đề kiểm tra 1 tiết Toán 9 Chương 4 Đại số có đáp án
-
496 lượt thi
-
13 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Phần trắc nghiệm
Nội dung câu hỏi 1
Đồ thị hàm số y = a đi qua điểm A(2;-1) thì hệ số a là:
Xem đáp án
Đáp án là C
Câu 2:
Cho phương trình + (m + 2)x + m = 0. Giá trị của m để phương trình có 2 nghiệm cùng âm là:
Xem đáp án
Đáp án là A
Câu 3:
Trong các phương trình sau đây phương trình nào là phương trình bậc hai ẩn x?
Xem đáp án
Đáp án là C
Câu 5:
Biết tổng hai nghiệm của phương trình bằng 5 và tích hai nghiệm của phương trình bằng 4. Phương trình bậc hai cần lập là:
Xem đáp án
Đáp án là B
Câu 6:
Cho parabol (P): y = /4 và đường thẳng (d): y = -x - 1. Tọa độ giao điểm của (P) và (d) là:
Xem đáp án
Đáp án là A
Câu 7:
Phần tự luận
Nội dung câu hỏi 1
Cho hàm số y= - (P) và đường thẳng (d): y = 2mx - 5
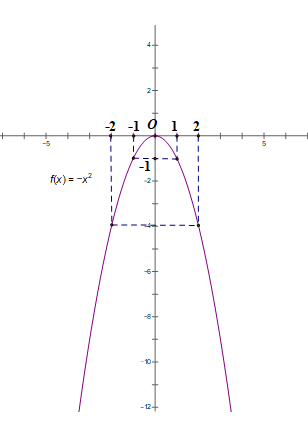
a) Vẽ đồ thị (P) của hàm số y = -
Xem đáp án
a) Lập bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y = - | -4 | -1 | 0 | -1 | -4 |
Đồ thị hàm số y = - là một đường parabol nằm phía dưới trục hoành, nhận trục Oy làm trục đối xứng, nhận gốc O (0; 0) làm đỉnh và là điểm cao nhất.
Câu 8:
Cho hàm số y= - (P) và đường thẳng (d): y = 2mx - 5
b) Chứng tỏ rằng trên mặt phẳng Oxy đường thẳng (d) và parabol (P) luôn cắt nhau tại hai điểm phân biệt. Tìm tọa độ hai giao khi m = 2.
Xem đáp án
b) Phương trình hoành độ giao điểm của (P) và (d) là:
- = 2mx - 5 ⇔ + 2mx - 5 = 0
Δ'= + 5 > 0 với ∀m ∈ R
Vậy trên mặt phẳng Oxy đường thẳng (d) và Parabol (P) luôn cắt nhau tại hai điểm phân biệt.
Khi m = 2, phương trình hoành độ giao điểm của (P) và (d) là:
-= 4x - 5 ⇔ + 4x - 5 = 0
Δ = - 4.1.(-5) = 36
⇒ Phương trình có 2 nghiệm
Vậy tọa độ hai giao điểm là M(1;-1) và N(-5;-25)
Câu 9:
Cho phương trình bậc hai + 4x + m = 0 (1)
a) Giải phương trình (1) khi m = -5.
Xem đáp án
a) Khi m = -5 ta được phương trình + 4x - 5 = 0
Ta có a + b + c = 1 + 4 + (-5) = 0 nên phương trình có hai nghiệm phân biệt là = 1; = c/a = (-5)/1 = -5
Tập nghiệm của phương trình S = {1; -5}
Câu 10:
Cho phương trình bậc hai + 4x + m = 0 (1)
b) Xác định m để phương trình (1) có nghiệm kép.
Xem đáp án
b) Δ' = 2.2 - m = 4 - m
Phương trình có nghiệm kép ⇔ Δ'= 0 ⇔ 4 - m = 0 ⇔ m = 4
Câu 11:
Cho phương trình bậc hai + 4x + m = 0 (1)
c) Xác định m để phương trình (1) có hai nghiệm và thỏa mãn = 10.
Xem đáp án
c) Để phương trình (1) có hai nghiệm x1 và x2 ⇔ Δ' ≥ 0 ⇔ 4 - m ≥ 0 ⇔ m ≤ 4
Theo Vi-et ta có: 
Ta có: = 10 ⇔ - 2x1x2 = 10
⇔ - 2m = 10 ⇔ 16 - 2m = 10 ⇔ m = 3 (TM)
Vậy với m = 3 thì phương trình (1) có hai nghiệm thõa mãn: = 10
Câu 12:
Cho phương trình + 2(m + 5)x + 6m - 30 = 0.
a) Với giá trị nào của m thì phương trình có 2 nghiệm phân biệt
Xem đáp án
+ 2(m + 5)x + 6m - 30 = 0
a) Δ' = - ac = - (6m - 30)
= + 10m + 25 - 6m + 30 = + 4m + 55
= + 4m + 4 + 51 = + 51 > 0 ∀m
Vậy phương trình đã cho luôn có 2 nghiệm phân biệt với mọi m
Câu 13:
Cho phương trình + 2(m + 5)x + 6m - 30 = 0.
b) hãy tìm 1 hệ thức liên hệ giữa 2 nghiệm không phụ thuộc vào giá trị của m
Xem đáp án
b) Theo định lí Vi-et ta có:
⇒ 3( + ) + = -6(m + 5) + 6m - 30
= -6m - 30 + 6m - 30 = -60
Vậy hệ thức liên hệ giữa 2 nghiệm không phụ thuộc vào giá trị của m là
3( + ) +