42 câu hỏi trắc nghiệm thuộc Dạng 2: Góc nội tiếp- góc tạo bởi tiếp tuyến và dây cung có đáp án

Câu 1:

Cho đường tròn (O) có các dây cung AB, BC, CA. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây MN song song với BC và gọi S là giao điểm của MN và AC. Chứng minh SM = SC và SN = SA.

Xem đáp án

Trình bày lời giải

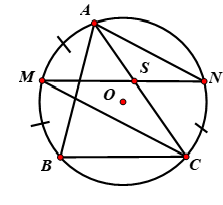
Cho đường tròn (O) có các dây cung AB, BC, CA. Gọi M là điểm chính giữa của cung nhỏ AB. (ảnh 1)

Do M là điểm chính giữa cung nhỏ AB nên sđ $\overset{⏜}{M B} =$ sđ $\overset{⏜}{M A}$

Do MN // BC nên $\hat{N M C} = \hat{M C B}$ $\Rightarrow$ sđ $\overset{⏜}{M B}$ = sđ $\overset{⏜}{N C}$

Vậy sđ sđ $\overset{⏜}{M B}$ =sđ $\overset{⏜}{N C}$

$\hat{N A S} = \hat{A N S}$ (hai góc nội tiếp cùng chắn hai cung bằng nhau)

$\hat{S M C} = \hat{S C M}$ (hai góc nội tiếp cùng chắn hai cung bằng nhau)

Vậy các tam giác ASN và MSC cân tại C

Nhận xét: Ở bài toán này học sinh có thể nhớ tới bài toán: Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau từ đó nhìn ra $\overset{⏜}{M B} = \overset{⏜}{C N}$

Câu 2:

Cho tam giác ABC nội tiếp đường tròn (O). Tia phân giác góc A cắt BC tại D và cắt đường tròn tại điểm thứ hai là M. Kẻ tiếp tuyến AK với đường tròn (M, MB), K là tiếp điểm. Chứng minh rằng DK vuông góc với AM.

Xem đáp án

Trình bày lời giải:

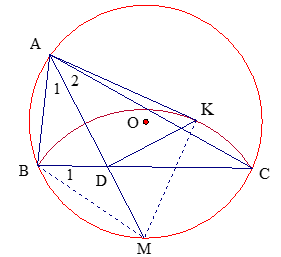
Cho tam giác ABC nội tiếp đường tròn (O). Tia phân giác góc A cắt BC tại D và cắt đường tròn tại điểm thứ hai là M. (ảnh 1)

$\hat{A_{1}} = \hat{A_{2}}$ mà $\hat{B_{1}} = \hat{A_{2}}$ ( góc nội tiếp) nên $\hat{B_{1}} = \hat{A_{1}}$ .

$Δ M B D ∽ Δ M A B$ (g.g) $\Rightarrow \frac{M D}{M B} = \frac{M B}{M A} \Rightarrow \frac{M D}{M K} = \frac{M K}{M A}$

Kết hợp với $\hat{D M K} = \hat{A M K}$ (góc chung)

ta có: $Δ D M K Δ K M A$ (c.g.c) $\Rightarrow \hat{MDK} = \hat{MKA} = 90^{°}$

Vậy DK ^AM.

Câu 3:

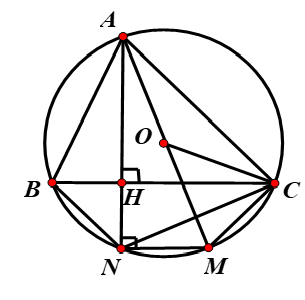
Cho tam giác ABC có ba góc nhọn, đường cao AH và nội tiếp đường tròn tâm O, đường kính AM.

a) Tính $\hat{A C M}$ ;

Xem đáp án

a) Ta có $\hat{A C M} = 90^{0}$ (góc nội tiếp).

Cho tam giác ABC có ba góc nhọn, đường cao AH và nội tiếp đường tròn tâm O, đường kính AM. a) Tính góc ACM ; (ảnh 1)

Câu 4:

b) Chứng minh $\hat{B A H} = \hat{O C A}$ ;

Xem đáp án

b) Vì $\hat{A B C} = \hat{A M C}$ (cùng chắn cung AC) và $\hat{A H B} = \hat{A C M} = 90^{0}$

Nên $Δ A B H$ và đồng dạng $Δ A M C$ ( g-g)

$\Rightarrow \begin{array}{l} \hat{B A H} = \hat{O A C} \\ \hat{O C A} = \hat{O A C} \end{array}\} \Rightarrow \hat{B A H} = \hat{O C A}$

Câu 5:

c) Gọi N là giao điểm AH với đường tròn (O). Tứ giác BCMN là hình gì? Vì sao?

Xem đáp án

c) $\hat{A N M} = 90^{0}$ , $A N ⊥ N M$ và nên MN // BC $\Rightarrow M N B C$ là hình thang

$B C / / M N \Rightarrow$ sđ $\overset{⏜}{B N} =$ sđ $\overset{⏜}{C M}$ (xem chứng minh Bài 1)

sđ $\overset{⏜}{B N} =$ sđ $\overset{⏜}{C N} \Rightarrow B M = C N$ $\Rightarrow M N B C$ là hình thang cân.

Câu 6:

Cho đường tròn tâm O và một dây AB của đường tròn đó. Các tiếp tuyến vẽ từ A và B của đường tròn cắt nhau tại C. Gọi D là một điểm trên đường tròn có đường kính OC ( D khác A và B). CD cắt cung AB của đường tròn (O) tại E. (E nằm giữa C và D). Chứng minh rằng:

a) $\hat{B E D} = \hat{D AE}$ .

Xem đáp án

a)

Cho đường tròn tâm O và một dây AB của đường tròn đó. Các tiếp tuyến vẽ từ A và B của đường tròn cắt nhau tại C. (ảnh 1)

Ta có : $\hat{EBC} = \hat{EAB}$ ; $\bar{DCB} = \hat{DAB}$ nên $\hat{EBC} + \hat{D C B} = \hat{E A B} + \hat{D A B}$ .

Mặt khác : $\hat{EBC} + \hat{DCB} = \hat{BED}, \hat{EAB} + \hat{DAB} = \hat{DAE}$ . Vậy $\hat{B E D} = \hat{D AE}$ .

Câu 7:

Chứng minh rằng:

b,

D E^{2} = D A . D B .

Xem đáp án

b) Ta có : $\hat{ADE} = \hat{ABC} = \hat{CAB} = \hat{EDB}$ mà theo câu a): $\hat{B E D} = \hat{D AE}$ , suy ra:

$Δ B E D ∽ Δ E A D$ (g-g) $\Rightarrow \frac{DE}{DA} = \frac{DB}{DE} \Rightarrow {DE}^{2} = DA . DB$

Câu 8:

Tam giác ABC nội tiếp đường tròn tâm O. Các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.

Xem đáp án

Trình bày lời giải:

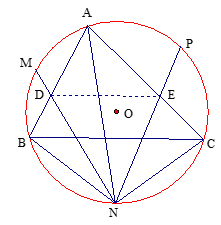
Tam giác ABC nội tiếp đường tròn tâm O. Các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. (ảnh 1)

$\overset{⏜}{A P} = \overset{⏜}{P C} \Rightarrow$ NE là đường phân giác của $Δ ANC \Rightarrow \frac{AE}{EC} = \frac{AN}{NC}$ (1)

$\overset{⏜}{A M} = \overset{⏜}{M B} \Rightarrow$ ND là đường phân giác của $Δ ANB \Rightarrow \frac{AD}{DB} = \frac{AN}{NB}$ (2)

$\overset{⏜}{B N} = \overset{⏜}{N C} \Rightarrow$ NB = NC (3)

Từ (1), (2) và (3) suy ra $\frac{AE}{EC} = \frac{AD}{DB}$ , do đó DE // BC.

Câu 9:

Từ điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB và một cát tuyến MCD. Gọi I là giao điểm của AB và CD. Chứng minh rằng: $\frac{I C}{I D} = \frac{M C}{M D}$ .

Xem đáp án

Trình bày lời giải

Từ điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB và một cát tuyến MCD. (ảnh 1)

Ta có $\hat{M A C} = \hat{A D C}$ (góc tạo bởi tiếp tuyến và dây cung); $\hat{AMD}$ chung. Suy ra $Δ M A C ∽ Δ M D A$ (g-g) suy ra: $M A^{2} = M C . M D$ và $\frac{M A}{M D} = \frac{A C}{A D}$

Tương tự: $Δ M B C ∽ Δ M D B$ suy ra: $\frac{M B}{M D} = \frac{B C}{B D}$

Xét $\frac{MC}{MD} = \frac{MC.MD}{{MD}^{2}} = \frac{{MA}^{2}}{{MD}^{2}} = \frac{MA}{MD} \cdot \frac{MB}{MD} = \frac{AC}{AD} \cdot \frac{BC}{BD} (1)$

Mặt khác : $Δ I A C ∽ Δ I D B$ suy ra: $\frac{I C}{I B} = \frac{A C}{B D}$

$Δ I B C ∽ Δ I D A$ suy ra: $\frac{I B}{I D} = \frac{B C}{A D}$ ;

Do đó: $\frac{AC}{AD} \cdot \frac{BC}{BD} = \frac{AC}{BD} \cdot \frac{BC}{AD} = \frac{IC}{IB} \cdot \frac{IB}{ID} = \frac{IC}{ID} (2)$

Từ (1) và (2) suy ra: $\frac{I C}{I D} = \frac{M C}{M D}$ .

Câu 10:

Gọi CA, CB lần lượt là các tiếp tuyến của đường tròn (O; R) với A, B là các tiếp điểm. Vẽ đường tròn tâm I qua C và tiếp xúc với AB tại B. Đường tròn (I) cắt đường tròn (O) tại M. Chứng minh rằng đường thẳng AM đi qua trung điểm của BC.

Xem đáp án

Trình bày lời giải

Gọi CA, CB lần lượt là các tiếp tuyến của đường tròn (O; R) với A, B là các tiếp điểm. (ảnh 1)

Gọi K là giao điểm của AM và BC.

Xét ∆KBM và ∆KAB có: $\overset{⏜}{K}$ chung; $\hat{K B M} = \hat{K A B}$ ( góc tạo bởi tia tiếp tuyến, dây cung và góc nội tiếp chắn cùng chắn cung của (O) )

Do đó: $Δ KBM Δ KAB \Rightarrow \frac{KB}{KA} = \frac{KM}{KB} \Rightarrow {KB}^{2} = KM.KA$ (1)

$\hat{MCK} = \hat{M B A}$ (góc tạo bởi tia tiếp tuyến dây cung và góc nội tiếp cùng chắn cung $\overset{⏜}{B M}$ của (I)).

$\hat{K A C} = \hat{M B A}$ (góc tạo bởi tia tiếp tuyến dây cung và góc nội tiếp cùng chắn cung $\overset{⏜}{A M}$ cuả (O)).

Do đó: $\hat{MCK} = \hat{KAC}$ . Xét ∆KCM và ∆KAC có: $\overset{⏜}{K}$ chung , $\hat{MCK} = \hat{KAC}$ . Do đó $Δ KCM Δ KAC \Rightarrow \frac{KC}{KA} = \frac{KM}{KC} \Rightarrow {KC}^{2} = KM.KA$ (2).

Từ (1) và (2) ta có: ${KC}^{2} = {KB}^{2} \Rightarrow KC = KB$ . Vậy AM đi qua trung điểm K của BC.

Câu 11:

Cho hình bình hành ABCD, góc A < 90⁰. Đường tròn ngoại tiếp tam giác BCD cắt AC ở E. Chứng mình rằng BD là tiếp tuyến của đường tròn ngoại tiếp tam giác AEB.

Xem đáp án

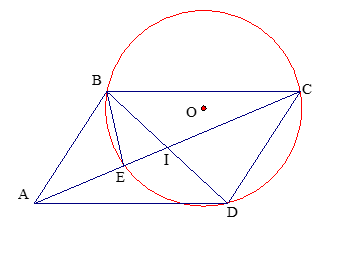
Cho hình bình hành ABCD, góc A < 900. Đường tròn ngoại tiếp tam giác BCD cắt AC ở E. (ảnh 1)

Gọi I là giao điểm hai đường chéo của hình bình hành.

IA = IC Þ $I E . I A = I E . I C$

$Δ I B E Δ I C D$ (g.g) Þ $I E . I C = I B . I D$

Từ đó suy ra: IE.IA = IE.IC = IB.ID = IB² . $\Rightarrow \frac{I B}{I E} = \frac{I A}{I B}$

Ta có ∆IBE và ∆IAB có $\frac{I B}{I E} = \frac{I A}{I B}$ và $\hat{BIA}$ chung , suy ra $Δ I B E Δ I A B$ (c.g.c) nên $\hat{I B E} = \hat{IAB}$ .

Suy ra BD là tiếp tuyến của đường tròn ngoại tiếp tam giác AEB( định lí bổ sung)

Câu 12:

Mỗi khẳng định sau đúng hay sai:

A. Góc tạo bởi tia tiếp tuyến và dây cung luôn nhỏ hơn 90⁰.

B. Trong một đường tròn, các góc nội tiếp bằng nhau chắn các cung bằng nhau.

C. Góc vuông nội tiếp thì chắn nửa đường tròn.

D. Góc tù nội tiếp thì có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.

Xem đáp án

Chọn đáp án A

Câu 13:

Cho hình vẽ, biết AB là đường kính của đường tròn (O), xy là tiếp tuyến của đường tròn tại A. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

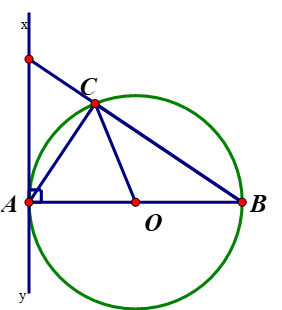
Cho hình vẽ, biết AB là đường kính của đường tròn (O), xy là tiếp tuyến của đường tròn tại A. (ảnh 1)

A. Góc CAx là góc tạo bởi tia tiếp tuyến và dây cung.

B. Góc BAy là góc tạo bởi tia tiếp tuyến và dây cung

C. Góc ACB là góc tù.

D. $\hat{C A x} < \hat{B C O}$

Xem đáp án

Chọn đáp án B

Câu 14:

Ghép mỗi ý ở cột bên trái với mỗi ý ở cột bên phải để được khẳng định đúng

A. Góc nội tiếp là góc	1) có số đo bằng 90⁰
B. Góc nội tiếp chắn nửa đường tròn	2) bằng nhau.
C. Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì	3) có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn.
D. Trong một đường tròn, hai góc nội tiếp không bằng nhau, góc lớn hơn thì	4) chắn dây lớn hơn.
	5) có cung bị chắn lớn hơn.

Xem đáp án

Nối: A – 3; B – 1; C – 2; D – 5

Câu 15:

Tam giác ABC nội tiếp (O;R). Tia phân giác của góc A cắt (O) tại M. Tia phân giác góc ngoài tại đỉnh A cắt (O) tại N. CMR:

a) Tam giác MBC cân.

Xem đáp án

a) Chứng minh rằng tam giác MBC cân

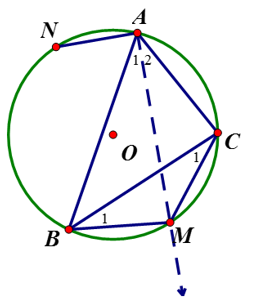
Tam giác ABC nội tiếp (O;R). Tia phân giác của góc A cắt (O) tại M. Tia phân giác góc ngoài tại đỉnh A cắt (O) tại N. CMR: (ảnh 1)

Có $\hat{A_{1}} = \hat{C_{1}}$ ; $\hat{A_{2}} = \hat{B_{1}}$ . Mà $\hat{A_{1}} = \hat{A_{2}}$ => $\hat{C_{1}} = \hat{B_{1}}$ . Vậy tam giác MBC cân tại M.

Câu 16:

b,3 điểm M, O, N thẳng hàng.

Xem đáp án

b) Chứng minh ba điểm M; O; N thẳng hàng:

Có AM và AN là 2 tia phân giác của hai góc kể bù

=> AM $⊥$ AN => $\hat{M A N} = 90^{0}$ => MN là đường kính của (O)

=> M; O; N thẳng hàng.

Câu 17:

Cho (O) và hai dây AB, CD bằng nhau và cắt nhau tại M. ( C thuộc cung nhỏ AB, B thuộc cung nhỏ CD).

a) CMR: cung AC = cung DB.

Xem đáp án

a)

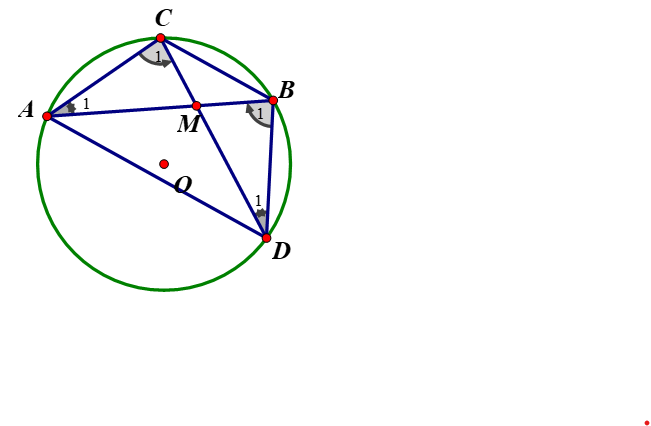
Cho (O) và hai dây AB, CD bằng nhau và cắt nhau tại M. ( C thuộc cung nhỏ AB, B thuộc cung nhỏ CD). a) CMR: cung AC = cung DB. (ảnh 1)

Chứng minh rằng: $\overset{⏜}{A C} = \overset{⏜}{D B}$

- Có sđ $\overset{⏜}{A C}$ + sđ $\overset{⏜}{C B}$ = sđ $\overset{⏜}{A B}$

- Có sđ $\overset{⏜}{B D}$ + sđ $\overset{⏜}{C B}$ = sđ $\overset{⏜}{D C}$

ð $\overset{⏜}{A C} = \overset{⏜}{D B}$ .

Câu 18:

b, CMR: ∆MAC = ∆MDB.

Xem đáp án

b, Chứng minh ∆MAC = ∆MDB.

- Có $\hat{C_{1}} = \hat{B_{1}}$ ; AC = BD; $\hat{A_{1}} = \hat{D_{1}}$

\Rightarrow

∆MAC = ∆MDB

Câu 19:

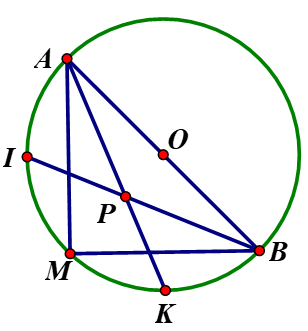
Cho (O) và hai dây MA và MB vuông góc với nhau. Gọi I, K lần lượt là điểm chính giữa của các cung nhỏ MA, MB. Gọi P là giao điểm của AK và BI.

a) CMR: A, O, B thẳng hàng.

Xem đáp án

a) Chứng minh rằng 3 điểm A; O; B thẳng hàng.

Cho (O) và hai dây MA và MB vuông góc với nhau. Gọi I, K lần lượt là điểm chính giữa của các cung nhỏ MA, MB. (ảnh 1)

Câu 20:

b, CMR: P là tâm đường tròn nội tiếp ∆MBA.

Xem đáp án

b, CMR: P là tâm đường tròn nội tiếp ∆MBA.

- Có I là điểm chính giữa cung nhỏ AM; K là điểm chính giữa cung nhỏ BM => AK; BI lần lượt là tia phân giác của các góc MAB và MBA của tam giác MBA => P là tâm đường tròn nội tiếp tam giác MBA.

Câu 21:

c, Giả sử MA = 12cm, MB = 16cm, tính bán kính đường tròn nội tiếp ∆MBA.

Xem đáp án

c, Giả sử MA = 12cm, MB = 16cm, tính bán kính đường tròn nội tiếp ∆MBA.

Giả sử r là bán kính đường tròn nội tiếp ∆MBA, a là độ dài cạnh huyền, p là nửa chu vi ∆MBA. Ta có: r = p – a

Câu 22:

Cho tam giác ABC nhọn nội tiếp đường tròn (O). Tia phân giác của góc A cắt (O) tại M.
a) CMR : tam giác BMC cân.

Xem đáp án

Chứng minh rằng : tam giác BMC cân

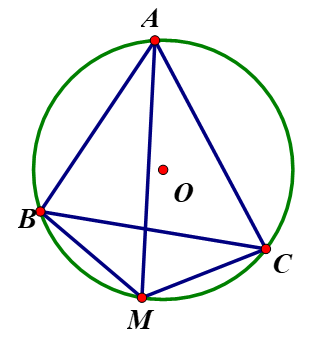
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Tia phân giác của góc A cắt (O) tại M. a) CMR : tam giác BMC cân. (ảnh 1)

- Có AM là tia phân giác của góc BAC => $\overset{⏜}{B M} = \overset{⏜}{M C}$ => BM = MC => tam giác BMC cân

Câu 23:

b, CMR : góc BMC = góc ABC + góc ACB.

Xem đáp án

b, Chứng minh rằng: $\hat{B M C} = \hat{A B C} + \hat{A C B}$

- Có $\hat{B M C} = \hat{A B C} + \hat{A C B}$

Mà: $\hat{B M A} = \hat{A C B}; \hat{A M C} = \hat{A B C}$

ð $\hat{B M C} = \hat{A B C} + \hat{A C B}$

Câu 24:

c, Gọi D là giao điểm của AM và BC. CMR : AB. AC = AD. AM; MD. MA = MB².

Xem đáp án

c, Gọi D là giao điểm của AM và BC. CMR : AB. AC = AD. AM; MD. MA = MB².

- ∆ABD ~ ∆AMC => AB. AC = AD. AM

∆MBD ~ ∆MAB => MD. MA = MB²

Câu 25:

Cho nửa đường tròn (O) đường kính CB, A thuộc nửa đường tròn sao cho AB < AC. Tiếp tuyến tại A cắt đường thẳng BC ở I. Kẻ AH vuông góc với BC. CMR:

a) AB là tia phân giác của góc IAH.

Xem đáp án

a, CMR: AB là tia phân giác của $\hat{I A H}$

- $\hat{I A B} = \hat{A C B}$ ( góc nội tiếp, góc tạo bởi tia tiếp tuyến và dây cung)

ð $\hat{B A H} = \hat{A C B}$ (cùng phụ với $\hat{A B H}$ )

\Rightarrow \hat{I A B} = \hat{B A H}

Câu 26:

b, IA² = IB. IC.

Xem đáp án

b, CMR: IA² = IB. IC: Có ∆IAB ~ ∆ICA => IA² = IB. IC

Câu 27:

Cho tam giác ABC vuông tại A, đường cao AH. Vẽ (I) đường kính BH cắt AB ở M. Vẽ (K) đường kính CH cắt AC ở N.

a) Tứ giác AMHN là hình gì ? CM ?

Xem đáp án

a,

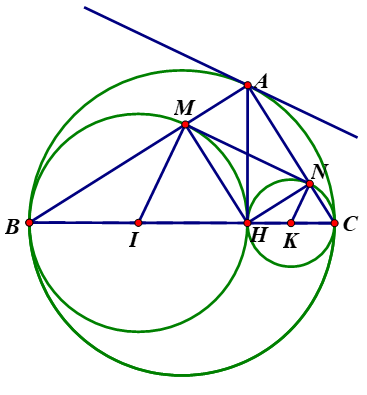
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ (I) đường kính BH cắt AB ở M. (ảnh 1)

Tứ giác AMHN là hình gì ? CM ?

Tứ giác AMHN là hình chữ nhật.

Câu 28:

b) CMR : MN là tiếp tuyến chung của hai đường tròn (I) và (K) ?

Xem đáp án

b, CMR: MN là tiếp tuyến chung của hai đường tròn (I) và (K).

- Có AMHN là hình chữ nhật

=> $\hat{N M H} = \hat{A H M}$

=> $\hat{N M H} = \hat{M B H}$ => MN là tiếp tuyến của (I)

- Chứng minh tương tự ta có MN là tiếp tuyến của (K).

Câu 29:

c, Vẽ tiếp tuyến Ax của đường tròn ngoại tiếp tam giác ABC. CMR : Ax // MN.

Xem đáp án

c, Có Ax là tiếp tuyến của (O) => $\hat{x A B} = \hat{A C B}$

=> $\hat{A C B} = \hat{N H A} = \hat{N M A}$ => $\hat{x A B} = \hat{N M A}$ => Ax // MN

Câu 30:

Trên nửa đường tròn (O) đường kính AB, lấy hai điểm M và N sao cho cung AM = cung MN = cung NB. Gọi P là giao điểm của AM và BN ; H là giao điểm của AN với BM. CMR :

a) Tứ giác AMNB là hình thang cân.

Xem đáp án

a,

Trên nửa đường tròn (O) đường kính AB, lấy hai điểm M và N sao cho cung AM = cung MN = cung NB. (ảnh 1)

Tứ giác AMNB là hình thang cân.

Tứ giác AMNB có MN // AB => AMNB là hình thang.

Lại có: AN = BM => AMNB là hình thang cân.

Câu 31:

Trên nửa đường tròn (O) đường kính AB, lấy hai điểm M và N sao cho cung AM = cung MN = cung NB. Gọi P là giao điểm của AM và BN ; H là giao điểm của AN với BM. CMR :

a) Tứ giác AMNB là hình thang cân.

Xem đáp án

a,

Tứ giác AMNB là hình thang cân.

Tứ giác AMNB có MN // AB => AMNB là hình thang.

Lại có: AN = BM => AMNB là hình thang cân.

Câu 32:

b, 4 điểm P, M, H, N cùng thuộc một đường tròn.

Xem đáp án

b, 4 điểm P, M, H, N cùng thuộc một đường tròn.

Có $\hat{A M B} = 90^{0} = > \hat{P M H} = 90^{0}$ => P; M; H cùng thuộc đường tròn đường kính PH.

Có $\hat{A N B} = 90^{0} = > \hat{P N H} = 90^{0}$ => P; N; H cùng thuộc đường tròn đường kính PH.

ð P; M; N; H cùng thuộc đường tròn đường kính PH.

Câu 33:

c, PH vuông góc với AB.

Xem đáp án

c, PH vuông góc với AB

Có H là trực tâm tam giác PAB => PH vuông góc với AB.

Câu 34:

d, 4 điểm P, M, H, N cùng thuộc một đường tròn.

Xem đáp án

d, ON là tiếp tuyến của đường tròn đường kính PH.

Có

\hat{O N A} = \hat{N P H} = \frac{1}{2}

sđ

\overset{⏜}{N H}

của đường tròn đi qua 4 điểm P; M; H; N mà cung NH nằm trong góc ONH => góc ONH là góc tạo bởi tia tiếp tuyến và dây cung chắn cung NH => ON là tia tiếp tuyến của đường tròn đi qua 4 điểm P; M; H; N

Câu 35:

Cho (O) và (O’) bằng nhau, cắt nhau tại A và B. Qua B vẽ một cát tuyến cắt các đường tròn (O) và (O’) lần lượt tại C và D.

a) CMR : AC = AD.

Xem đáp án

a,

CMR : AC = AD.

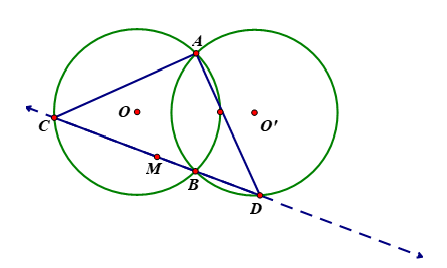
Cho (O) và (O’) bằng nhau, cắt nhau tại A và B. Qua B vẽ một cát tuyến cắt các đường tròn (O) và (O’) lần lượt tại C và D. (ảnh 1)

(O) có góc ACB là góc nội tiếp chắn cung nhỏ A_mB.

(O’) có góc ADB là góc nội tiếp chắn cung nhỏ A_nB

(O) và (O’) bằng nhau

ð $\hat{A C B} = \hat{A D B}$ => ∆ACD cân tại A

\Rightarrow

AC = AD.

Câu 36:

b, Tìm quỹ tích trung điểm M của CD khi cát tuyến CBD quay quanh B.

Xem đáp án

b, Tìm quỹ tích trung điểm M của CD khi cát tuyến CBD quay quanh B.

Tam giác ACD cân tại A có M là trung điểm của CD => AM vuông góc với CD

=>

\hat{A M B} = 90^{0}

M thuốc đường tròn đường kính AB.

Câu 37:

Cho (O) đường kính AB; C chạy trên một nửa đường tròn. Vẽ đường tròn tâm I tiếp xúc với đường tròn (O) tại C, tiếp xúc với đường kính AB tại D. Đường tròn này cắt CA, CB lần lượt tại M và N.

a) CMR: 3 điểm M, I, N thẳng hàng .

Xem đáp án

a) CMR: 3 điểm M, I, N thẳng hàng

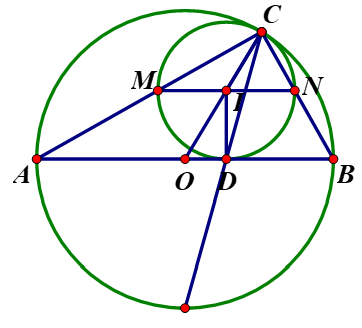
Cho (O) đường kính AB; C chạy trên một nửa đường tròn. Vẽ đường tròn tâm I tiếp xúc với đường tròn (O) tại C, tiếp xúc với đường kính AB tại D. (ảnh 1)

Có $\hat{A C B} = 90^{0}$ => $\hat{M C N} = 90^{0}$ => MN là đường kính của (I) => M; I; N thẳng hàng.

Câu 38:

b, CMR:ID vuông góc với MN .

Xem đáp án

b, CMR:ID vuông góc với MN.

Có AB là tiếp tuyến của (I) tại D => ID vuông góc với AB.

Có MN // AB => ID vuông góc với MN.

Câu 39:

c, CMR: đường thẳng CD đi qua một điểm cố định.

Xem đáp án

c, CMR: đường thẳng CD đi qua một điểm cố định.

Chứng minh CD là tia phân giác của góc ACB => CD đi qua điểm chính giữa của cung AB.

Câu 40:

d, Suy ra cách dựng đường tròn (I) nói trên.

Xem đáp án

d, Suy ra cách dựng đường tròn (I) nói trên

Câu 41:

Cho đường tròn (O) ngoại tiếp tam giác ABC, từ điểm M trên cung BC không chứa điểm A, hạ các đường vuông góc với BC; CA; AB lần lượt tại D; H; K. Chứng minh rằng: $\frac{B C}{M D} = \frac{C A}{M H} + \frac{A B}{M K}$

Xem đáp án

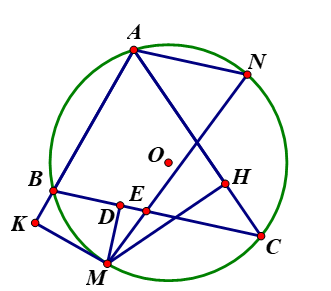
Cho đường tròn (O) ngoại tiếp tam giác ABC, từ điểm M trên cung BC không chứa điểm A, (ảnh 1)

Từ A kẻ đường thẳng song song với BC cắt (O) tại N => AB = NC => $\hat{B M N} = \hat{A M C}$

Gọi E là giao điểm của BC và MN;

\hat{C B M} = \hat{C A M}; \hat{B E M} = \frac{1}{2}

sđ

(\overset{⏜}{B M} + \overset{⏜}{C N})

= \frac{1}{2}

sđ

(\overset{⏜}{B M} + \overset{⏜}{A B}) = \hat{A C M}

ð ∆BME ~ ∆AMC, có MH và MD là 2 đường cao tương ứng=> $\frac{A C}{M H} = \frac{B E}{M D}$ (1)

$\hat{M C B} = \hat{M A B}; \hat{C M N} = \hat{A M B} (\overset{⏜}{N C} = \overset{⏜}{A B})$

ð ∆CME ~ ∆AMB; có MD; MK là 2 đường cao tương ứng => $\frac{C E}{M D} = \frac{A B}{M K}$ (2)

Từ (1) và (2) => $\frac{A C}{M H} + \frac{A B}{M K} = \frac{B E}{M D} + \frac{C E}{M D} = \frac{B C}{M D}$

Câu 42:

Hai đường tròn (O) và (O’) cắt nhau tại A và B. Các điểm M và N theo thứ tự di chuyển trên các đường tròn (O) và (O’) sao cho chiều từ A đến M và từ A đến N trên các đường tròn (O) và (O’) đều theo chiều quay của kim đồng hồ và các cung AM và AN có số đo bằng nhau. Chứng minh rằng đường trung trực của MN luôn đi qua một điểm cố định.

Xem đáp án

Kẻ các đường kính BOC, BO’D thì C; A; D thẳng hàng, CAD là cát tuyến chung cố định.

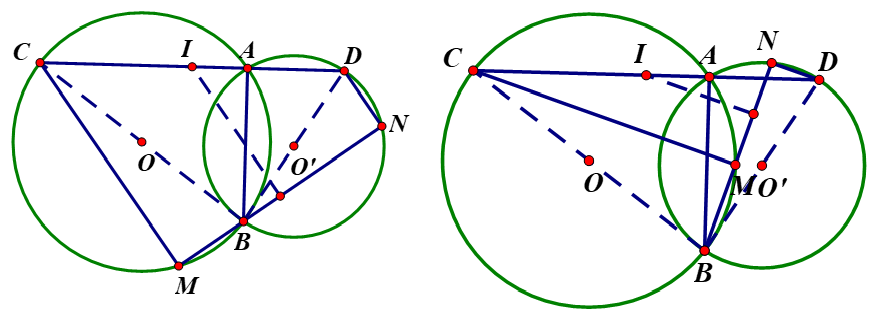
Hai đường tròn (O) và (O’) cắt nhau tại A và B. Các điểm M và N (ảnh 1)

Trường hợp M thuộc cung BC không chứa A ( Ha): $\hat{A B N} = \hat{A C M}$ , $\hat{A C M}$ bù $\hat{A B M}$ nên $\hat{A B N}$ bù $\hat{A B M}$ , do đó M; B; N thẳng hàng.

Trường hợp M thuộc cung BC có chứa A (Hb): $\hat{A B N} = \hat{A B M}$ nên M; B; N thẳng hàng.

Trong cả hai trường hợp, ta có CM và DN cùng vuông góc với MN. Do đó đường trung trực của MN luôn đi qua trung điểm I của CD, đó là điểm cố định.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập Toán 9 Chủ đề 2: Góc với đường tròn có đáp án

Dạng 2: Góc nội tiếp- góc tạo bởi tiếp tuyến và dây cung có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương