3 câu hỏi trắc nghiệm thuộc Dạng 2: Chứng minh các điểm cùng thuộc một đường tròn có đáp án

Bài tập Toán 9 Chủ đề 3: Tứ giác nội tiếp có đáp án

Dạng 2: Chứng minh các điểm cùng thuộc một đường tròn có đáp án

568 lượt thi
3 câu hỏi
50 phút

Danh sách câu hỏi

Câu 1:

Cho hình thoi ABCD có góc A bằng $60 °$ , AB = a. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng 6 điểm E, F, G, H, B, D cùng nằm trên một đường tròn. Xác định tâm và tính bán kính của đường tròn đó theo a.

Xem đáp án

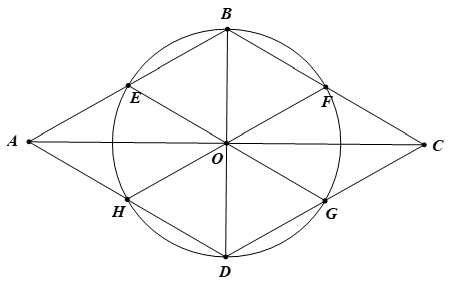
Cho hình thoi ABCD có góc A bằng 60 độ , AB = a. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. (ảnh 1)

Gọi O là giao điểm của AC và BD ta có OB = OD

Do ABCD là hình thoi nên ta có $A C ⊥ B D$ .

Ta có $\hat{B A D} = 60^{0}$ nên $\hat{B A O} = 30^{0}$ (tính chất đường chéo hình thoi)

Tam giác ABO vuông tại O có

$O B = A B s i n \hat{B A O} \Rightarrow O B = a . \sin 30^{0} = \frac{a}{2}$

Xét tam giác vuông ABO có $\hat{A B O} + \hat{B A O} = 90^{0}$ ( hai góc phụ nhau) mà $\hat{B A O} = 30^{0}$ suy ra $\hat{A B O} = 60^{0}$ hay $\hat{E B O} = 60^{0}$

$O E = \frac{1}{2} A B = E B = E A$ ( tính chất đường trung tuyến trong tam giác vuông và E là trung điểm của AB.

Tam giác EOB là tam giác cân tại E có $\hat{E B O} = 60^{0}$ nên tam giác EBO là tam giác đều $\Rightarrow O E = O B$

Chứng minh tương tự với các tam giác vuông BOC, COD và DOA ta có :

$O E = O B = O F = O C = O G = O D = O H$

Vậy 6 điểm E, F, G, H, B, D cùng nằm trên một đường tròn tâm O. Bán kính $O B = \frac{a}{2}$

Câu 2:

Cho tam giác ABC vuông tại A. Trên AC lấy điểm D. Hình chiếu của D lên BC là E, điểm đối xứng của E qua BD là F. Chứng minh 5 điểm A, B, E, D, F cùng nằm trên một đường tròn. Xác định tâm O của đường tròn đó.

Xem đáp án

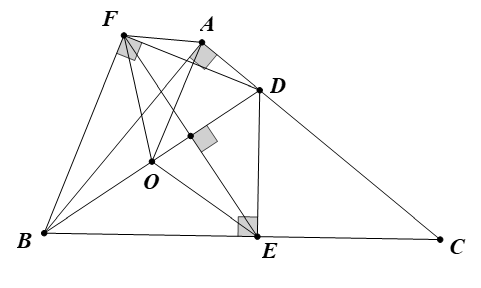
Cho tam giác ABC vuông tại A. Trên AC lấy điểm D. Hình chiếu của D lên BC là E, điểm đối xứng của E qua BD là F. (ảnh 1)

Do $D E ⊥ B C \Rightarrow \hat{D B E} = 90^{0}$

Vì E và F đối xứng với nhau qua BD nên BD là đường trung trực của đoạn thẳng EF

$\Rightarrow B F = B E; D F = D E$

$Δ B F D = Δ B E D$ (c-c-c) $\Rightarrow \hat{B F D} = \hat{B E D} = 90^{0}$

Gọi O là trung điểm của BD.

Xét tam giác vuông ABD vuông tại A có AO là trung tuyến nên $A O = \frac{1}{2} B D = O B = O D (1)$

Tam giác vuông BDE vuông tại E có OE là trung tuyến nên $E O = \frac{1}{2} B D = O B = O D (2)$

Tam giác vuông BFDvuông tại F có OF là trung tuyến nên $F O = \frac{1}{2} B D = O B = O D (3)$

Từ $(1), (2), (3) \Rightarrow O A = O B = O D = O E = OF$ . Vậy 5 điểm A, B, E, D, F cùng nằm trên một đường tròn tâm O với O là trung điểm của BC.

Câu 3:

Từ một điểm A ở ngoài đường tròn (O) vẽ các tiếp tuyến AB, AC. Cát tuyến ADE không đi qua tâm O (D nằm giữa A và E). Gọi I là trung điểm của DE.

Chứng minh 5 điểm O,B,A,C,I cùng thuộc một đường tròn.

Xem đáp án

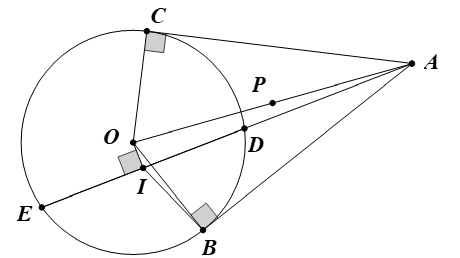
Từ một điểm A ở ngoài đường tròn (O) vẽ các tiếp tuyến AB, AC. Cát tuyến ADE không đi qua tâm O (D nằm giữa A và E). (ảnh 1)

Do AC và AB là các tiếp tuyến nên

$\hat{O C A} = \hat{O B A} = 90^{0}$

Do I là trung điểm của ED nên $O I ⊥ E D$

(đường kính đi qua trung điểm của dây thì vuông góc với dây cung)

hay $\hat{O I D} = \hat{O I A} = 90^{0}$

Gọi P là trung điểm của OA

Xét tam giác vuông OCA có CP là đường trung tuyến nên $C P = \frac{1}{2} A O = O P = P A$

Xét tam giác vuông OBA có BP là đường trung tuyến nên $B P = \frac{1}{2} A O = O P = P A$

Xét tam giác vuông OIA có IP là đường trung tuyến nên $I P = \frac{1}{2} A O = O P = P A$

Vậy $O P = P A = P C = P I = P B$ nên 5 điểm O,B,A,C,I cùng thuộc một đường tròn.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập Toán 9 Chủ đề 3: Tứ giác nội tiếp có đáp án

Dạng 2: Chứng minh các điểm cùng thuộc một đường tròn có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương