Thứ hai, 23/12/2024
Đăng ký Đăng nhập
IMG-LOGO
Trang chủ Lớp 9 Toán Bài tập Toán 9 Chủ đề 5: Bài toán chứng minh ba điểm thẳng hàng có đáp án

Bài tập Toán 9 Chủ đề 5: Bài toán chứng minh ba điểm thẳng hàng có đáp án

Dạng 2: Sử dụng tính chất đường chéo của hình đặc biệt (vd: hình bình hành) có đáp án

  • 1120 lượt thi

  • 9 câu hỏi

  • 50 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho ∆ABC có trực tâm H nội tiếp (O) đường kính CM, gọi I là trung điểm của AB. Chứng minh rằng H, I, M thẳng hàng.
Xem đáp án
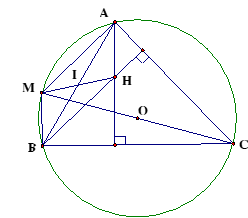
Cho  tam giác ABCcó trực tâm H nội tiếp (O) đường kính CM, gọi I là trung điểm của AB. Chứng minh rằng H, I, M thẳng hàng. (ảnh 1)

MB⊥BC, AH⊥BC (suy từ giả thiết).

⇒MB//AH.

Mà MA//BH (cùng vuông góc với AC).

⇒AMBH là hình bình hành.

⇒AB cắt MH tại trung điểm I của AB và MH  (t/c hình bình hành).

Suy ra H, I, M thẳng hàng.

Câu 2:

Cho nửa đường tròn đường kính AB trên đó có một điểm M. Trên đường kinh AB lấy một điểm C sao cho AC<CB . Trên nửa mặt phằng bờ AB có chứa điểm M, người ta kẻ các tia Ax, By vuông góc với AB; đường thẳng qua M vuông góc với MC cắt Ax tại P; đường thẳng qua C vuông góc với CP cắt By tại Q. Gọi D là giao điểm của CP và AM; E là giao điểm của CQ và BM

a) Chứng minh rằng các tứ giác ACMP, CDME nội tiếp được
Xem đáp án
a)
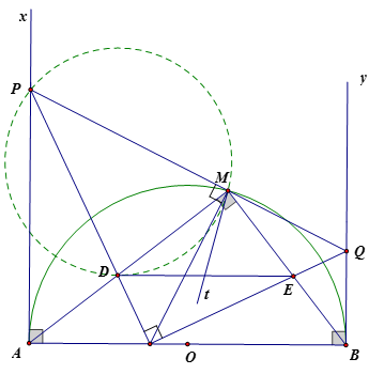
Cho nửa đường tròn đường kính AB trên đó có một điểm M. Trên đường kinh AB lấy một  điểm C (ảnh 1)
Tứ giác ACMP có A^=M^=900  nên nội tiếp được
Tứ giác CDME có C^=M^=900   nên nội tiếp được

Câu 3:

b) Chứng minh rằng hai đường thẳng AB, DE song song
Xem đáp án
b) Do các tứ giác ACMP và CDME nội tiếp được nên MAC^=MPC^ , MDE^=MCE^  mà MPC^=MCE^  ( vì cùng phụ với góc MCP^ ) nên MAC^=MDE^ . Vậy AB song song với DE

Câu 4:

c) Chứng minh rằng ba điểm P,M, Q thẳng hàng
Xem đáp án
c) Do  MBQ^=MAC^( vì cùng phụ ABM^ ) và MAC^=MDE^=MCQ^  nênMCQ^=MBQ^ . Suy ra tứ giác CMQB nội tiếp do đó CMQ^=900 . Vậy P, M, Q thẳng hàng

Câu 5:

d) Ngoài điểm M ra, các đường tròn ngoại tiếp các tam giác DMP, EMQ còn điểm chung nào nữa không? Vì sao?
Xem đáp án

d) Trên nửa mặt phẳng bờ MC không chứa điểm D , kẻ tia tiếp tuyến Mt của đường tròn ngoại tiếp tam giác DMP suy ra AMt^=MPD^  màMQC^ phụ với  MPC^ nên BMt^=MQC^ . Suy ra Mt tiếp xúc với đường tròn ngoại tiếp tam giác EMQ. Do đó hai đường tròn ngoại tiếp các tam giác DMP và EMQ tiếp xúc nhau. Vậy có duy nhất một điểm M là điểm chung của hai đường tròn nói trên

Câu 6:

Cho đường tròn (O) đường kính AB=2R và một điểm C trên đường tròn (C không trùng với A và B. Trên nửa mặt phẳng bờ AB có chứa điểm C, kẻ tia Ax tiếp xúc với đường tròn (O). Gọi M là điểm chính giữa cung nhỏ AC; P là giao điểm của AC, BM. Tia BC cắt các tia AM, Ax lần lượt tại N và Q
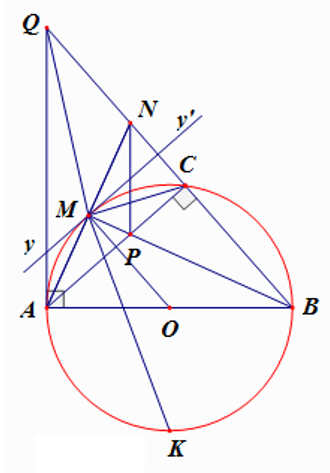
a) Chứng minh tam giác ABN cân
Xem đáp án
a)
 Media VietJack
Tam giác ABN có đường cao BM đồng thời là đường phân giác nên tam giác ABN cân tại B.

Câu 7:

b) Tứ giác APNQ là hình gì? Vì sao?
Xem đáp án

b) Vì P là trực tâm tam giác ABN nên NP ⊥  AB ⇒  NP // AQ, do đó APNQ là hình thang.

Câu 8:

c) Gọi K là điểm chính giữa của cung AB không chứa C. Hỏi có thể xảy ra ba điểm Q, M, K thẳng hàng không? Vì sao?
Xem đáp án

c) Nếu Q , M , K thẳng hàng thì từ tính chất góc có đỉnh bên ngoài đường tròn, ta có QM là đường phân giác của góc AQB. Mặt khác , BM là phân giác của góc ABQ nên AM là phân giác của góc BAQ, vô lý. Vậy ba điểm Q , M , K không thẳng hàng.

Câu 9:

d) Xác định vị trí của điểm C để đường tròn ngoại tiếp tam giác MNQ tiếp xúc với đường tròn (O).
Xem đáp án

d) Tại điểm M, kẻ tiếp tuyến yMy’ với (O) sao cho My và MA cùng phía với đường thẳng MQ. Ta có đường tròn ngoại tiếp tam giác MNQ tiếp xúc với (O) khi và chỉ khi yMy’ tiếp xúc với đường tròn ngoại tiếp tam giác MNQ tại M. Điều đó tương đương với

NQM^=NMy'^⇔NQM^=AMy^⇔NQM^=ABM^⇔NQM^=MBC^

⇔MB=MQ⇔BC=NQ( vì ΔMNC  cân).

Mà AB2=BC.BQ⇔AB2=BC.BN+NQ⇔4R2=BC.2R+BC

⇔BC=R5−1.

Vậy BC=R5−1   thì đường tròn ngoại tiếp ΔMNQ  tiếp xúc với (O).

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương