15 câu hỏi trắc nghiệm thuộc Dạng 3: Sử dụng tính chất về tâm và đường kính của đường tròn có đáp án

Câu 1:

Cho (O) đường kính AB. Điểm M chuyển động trên (O), $M \neq A$ ; $M \neq B$ . Kẻ MH vuông góc với AB. Vẽ đường tròn $(O_{1})$ đường kính MH cắt đường thẳng MA và MB tại C và D . Chứng minh rằng:

a) C ,D , $O_{1}$ thẳng hàng.

Xem đáp án

a)

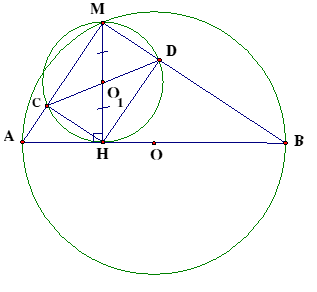
Cho (O) đường kính AB. Điểm M chuyển động trên (O), (ảnh 1)

Ta có : $\hat{A M B} = 90^{o}$

(góc nội tiếp chắn nửa (O)).

$\Rightarrow \hat{C M D} = 90^{o}$ . $\Rightarrow C D$ là đường kính của $(O_{1})$ .

Suy ra C, D, $O_{1}$ thẳng hàng.

Câu 2:

b, Chứng minh rằng: $A B C D$ nội tiếp

Xem đáp án

b) $M C H D$ là hình chữ nhật nội tiếp $(O)$ .

$\Rightarrow \hat{M C D} = \hat{M H D}$ ( 2 góc nội tiếp cùng chắn $\overset{⏜}{C D}$ ).

Mà $\hat{M C D} = \hat{B} \Rightarrow \hat{M C D} + \hat{A C D} = \hat{B} + \hat{A C D} = 180^{o}$ .

Vậy $A B C D$ nội tiếp.

Câu 3:

Cho tam giác vuông ABC nội tiếp đường tròn tâm O đường kính AB. Trên tia đối của tia CA lấy điểm D sao cho CD = AC
a) Chứng minh tam giác ABD cân

Xem đáp án

a)

Cho tam giác vuông ABC nội tiếp đường tròn tâm O đường kính AB. Trên tia đối của tia CA lấy điểm D sao cho CD = AC (ảnh 1)

Xét $Δ A B D$ có $B C ⊥ D A, C A = C D$ nên BC vừa là đường cao vừa là đường trung tuyến, do đó $Δ A B D$ cân tại B.

Câu 4:

b) Đường thẳng vuông góc với AC tại A cắt đường tròn (O) tại E. Trên tia đối của tia EA lấy điểm F sao cho EF= AE. Chứng minh ba điểm D, B, F thẳng hàng

Xem đáp án

b) $\hat{C A E} = 90^{0}$ nên CE là đường kính của đường tròn (O) C, O, E thẳng hàng.

Ta có CO là đường trung bình của tam giác ABD

CO//DB CE// BD.

Tương tự, OE là đường trung bình của

OE//BF CE//BF.

Suy ra B, D, F thẳng hàng ( theo tiên đề Owclit).

Câu 5:

c) Chứng minh đường tròn ngoại tiếp tam giác ADF tiếp xúc với đường tròn (O)

Xem đáp án

c) Theo tính chất đường trung bình của $Δ A B D; Δ A B F$ ta có $O C = \frac{1}{2} D B; O E = \frac{1}{2} B F$ mà $O C = O E \Rightarrow B D = B F = A B$

$\Rightarrow$ B là tâm đường tròn ngoại tiếp tam giác ADF $\to$ BA là bán kính.

Mà $O B = A B - O A$ nên đường tròn ngoại tiếp tam giác ADF tiếp xúc với đường tròn (O) tại A.

Câu 6:

Cho tam giác ABC vuông tại C và BC < CA. Gọi I là điểm trên AB và IB < IA. Kẻ đường thẳng d đi qua I và vuông góc với AB. Gọi giao điểm của d với AC, BC lần lượt là F và E. Gọi M là điểm đối xứng với B qua I.
a) Chứng minh rằng tam giác IME đồng dạng với tam giác IFA và IE. IF = IA. IB

Xem đáp án

a)

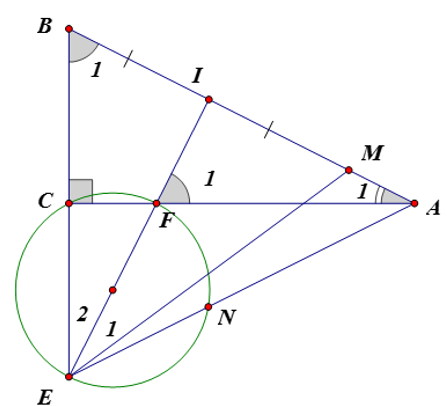
Cho tam giác ABC vuông tại C và BC < CA. Gọi I là điểm trên AB và IB < IA. Kẻ đường thẳng d đi qua I và vuông góc với AB. (ảnh 1)

Ta có IE là đường trung trực của BM

\Rightarrow Δ E B M

cân tại M

\Rightarrow \hat{B_{1}} = \hat{M_{1}}

Mà

\hat{B_{1}} = \hat{F_{1}}

( cùng phụ với

\hat{A_{1}}

)

Δ I M E Δ I F A (g . g) \Rightarrow \frac{I M}{I F} = \frac{I E}{I A} \Rightarrow I E . I F = I A . I M \Rightarrow I E . I F = I A . I B

Câu 7:

b) Đường tròn ngoại tiếp tam giác CEF cắt AE tại N. Chứng minh rằng F, N, B thẳng hàng.

Xem đáp án

b) Ta có $\hat{E C F} = 90^{0} \Rightarrow \hat{E N F} = 90^{0}$
Xét $Δ B A E$ có EI, AC là các đường cao cắt nhau tại F nên $B F ⊥ E A$ mà $F N ⊥ E A$ $\Rightarrow B, F, N$ thẳng hàng

Câu 8:

c) Cho AB cố định, C thay đổi sao cho $\hat{B C A} = 90^{0}$ . Chứng minh rằng đường tròn ngoại tiếp tam giác AEF luôn đi qua hai điểm cố định và tâm đường tròn này nằm trên đường thẳng cố định

Xem đáp án

c, Ta có

\hat{E_{1}} = \hat{A_{1}}

suy ra tứ giác AMFE nội tiếp
Từ đó suy ra đường tròn ngoại tiếp tam giác AEF luôn qua hai điểm A, M cố định. Vậy tâm đường tròn ngoại tiếp tam giác AEF luôn nằm trên đường trung trực của AM cố định

Câu 9:

Trên cạnh CD của hình vuông ABCD, lấy một điểm M, vẽ đường tròn tâm O đường kính AM. Gọi E là giao điểm của đường tròn tâm (O') đường kính CD. Hai đường tròn cắt nhau tại điểm thứ hai N. Tia DN cắt BC tại P. Chứng minh rằng:

a) Ba điểm $E, N, C$ thẳng hàng

Xem đáp án

a,

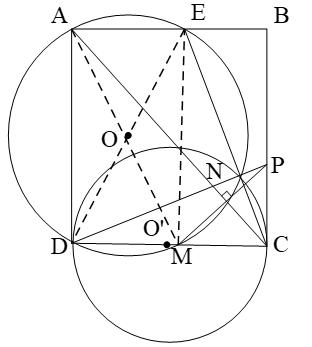
Trên cạnh CD của hình vuông ABCD, lấy một điểm M, vẽ đường tròn tâm O đường kính AM (ảnh 1)

Ta có D là giao điểm thứ nhất của (O) và (O')

Dễ thấy $A E M D$ là hình chữ nhật và ED là đường kính của (O)

Nên $\hat{E N D} = 90^{0}$ (góc nội tiếp chắn nửa cung đường tròn)

Mặt khác CD là đường kính của (O')

nên $\hat{D N C} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow \hat{E N D} + \hat{D N C} = 180^{0}$ hay ba điểm $E, N, C$ thẳng hàng.

Câu 10:

b, Chứng minh rằng:

C A ⊥ M P

Xem đáp án

Ta có $A E M D$ là hình chữ nhật

$\Rightarrow A E C M$ là hình chữ nhật

$\Rightarrow \overset{⏜}{E B} = \overset{⏜}{C M}$ (1)

Xét $Δ C B E$ và $Δ C D P$ có

$B C E = C D P$ (hai góc cùng phụ với góc $D P C$ )

$C B = D C; B = C = 90^{0}$ (gt)

Do đó: $Δ C B E = Δ D C P$ (g.c.g)

$\Rightarrow E B = C P$ (2)

Từ (1) và (2)

$\Rightarrow C M = C P$ hay $Δ P C M$ cân có là đường phân giác

$\Rightarrow C A$ cũng đồng thời là đường cao.

Vậy $C A ⊥ M P$ .

Câu 11:

Cho đường tròn (O), M là điểm ở ngoài (O), hai tiếp tuyến MAvà MB( A, B là hai tiếp tuyến), C là một điểm trên đường tròn tâm M bán kính MA và nằm trong đường tròn (O). Các tia AC và BC cắt đường tròn (O) lần lượt tại E và D.

Chứng minh ba điểm D,O,E thẳng hàng.

Xem đáp án

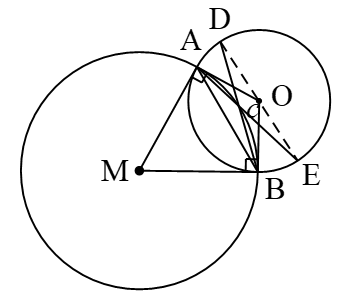
Cho đường tròn (O), M là điểm ở ngoài (O), hai tiếp tuyến MAvà MB( A, B là hai tiếp tuyến), (ảnh 1)

Trong đường tròn (O) ta có: $\hat{A B D} = \frac{1}{2} \hat{A O D}$

Mặt khác trong đường tròn (M) có:

$\hat{A B C} = \frac{1}{2} \hat{A M C}$ (góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung).

$\Rightarrow \hat{A M C} = \hat{A O D}$ (1)

Tương tự ta có: $\hat{B M C} = \hat{B O E}$ (2)

Do MA và MB là tiếp tuyến của (O) nên:

$\hat{M A O} = \hat{M B O} = 90^{0}$

Hay $\hat{M A O} = \hat{M B O} = 180^{0}$

$\Rightarrow \hat{A M B} + \hat{A O B} = 180^{0}$

Hay $\hat{A M C} + \hat{B M C} + \hat{A O B} = 180^{0}$ (3)

Từ (1), (2) và (3) ta có: $A O D + B O E + A O B = 180^{0}$

Vậy ba điểm $D, O, E$ thẳng hàng.

Câu 12:

Gọi M là một điểm bất kỳ trên đường tròn ngoại tiếp $∆ A B C$ ; P,Q,R lần lượt là hình chiếu của M trên các đường thẳng BC, CA và .

Chứng minh rằng:

a) Các điểm $M, B, P, R$ cùng thuộc một đường tròn.

Xem đáp án

a)

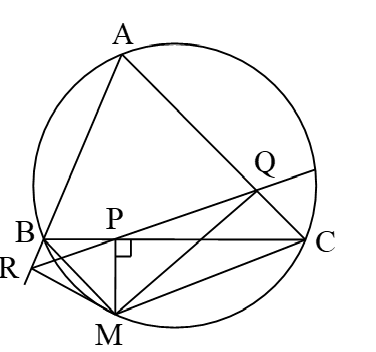
Gọi M là một điểm bất kỳ trên đường tròn ngoại tiếp tam giác ABC; P,Q,R lần lượt là hình chiếu của M trên các đường thẳng BC, CA và . (ảnh 1)

$\hat{B R M} + \hat{B P M} = 90^{0} + 90^{0} = 180^{0}$ Tứ giác $R B P M$ nội tiếp.

$\Rightarrow$ Các điểm $M, P, B, C$ cùng thuộc một đường tròn

Câu 13:

Chứng minh rằng: b) Các điểm R,P,Q thẳng hàng.

Xem đáp án

b) Chứng minh tương tự a) có tứ giác $M P Q C$ nội tiếp

$\Rightarrow \hat{M P Q} + \hat{M C Q} = 180^{0}$

Mà $\hat{R B M} = \hat{R P M}$ (tứ giác $R B P M$ nôi tiếp)

Và $\hat{R B M} = \hat{M C Q}$ (tứ giác $A B M C$ nội tiếp)

Do đó: $\hat{R P M} = \hat{M C Q}$

Ta có: $\hat{R P M} + \hat{M P Q} = \hat{M C Q} + \hat{M P Q} = 180^{0}$ $\Rightarrow R, P, Q$ thẳng hàng.

Câu 14:

Chứng minh rằng: b) Các điểm R,P,Q thẳng hàng.

Xem đáp án

b) Chứng minh tương tự a) có tứ giác $M P Q C$ nội tiếp

$\Rightarrow \hat{M P Q} + \hat{M C Q} = 180^{0}$

Mà $\hat{R B M} = \hat{R P M}$ (tứ giác $R B P M$ nôi tiếp)

Và $\hat{R B M} = \hat{M C Q}$ (tứ giác $A B M C$ nội tiếp)

Do đó: $\hat{R P M} = \hat{M C Q}$

Ta có: $\hat{R P M} + \hat{M P Q} = \hat{M C Q} + \hat{M P Q} = 180^{0}$ $\Rightarrow R, P, Q$ thẳng hàng.

Câu 15:

Chứng minh rằng: b) Các điểm R,P,Q thẳng hàng.

Xem đáp án

b) Chứng minh tương tự a) có tứ giác $M P Q C$ nội tiếp

$\Rightarrow \hat{M P Q} + \hat{M C Q} = 180^{0}$

Mà $\hat{R B M} = \hat{R P M}$ (tứ giác $R B P M$ nôi tiếp)

Và $\hat{R B M} = \hat{M C Q}$ (tứ giác $A B M C$ nội tiếp)

Do đó: $\hat{R P M} = \hat{M C Q}$

Ta có: $\hat{R P M} + \hat{M P Q} = \hat{M C Q} + \hat{M P Q} = 180^{0}$ $\Rightarrow R, P, Q$ thẳng hàng.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập Toán 9 Chủ đề 5: Bài toán chứng minh ba điểm thẳng hàng có đáp án

Dạng 3: Sử dụng tính chất về tâm và đường kính của đường tròn có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương