Luyện tập trang 77
-
1818 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Dựng góc nhọn α, biết:
Xem đáp án
Lời giải:
a)
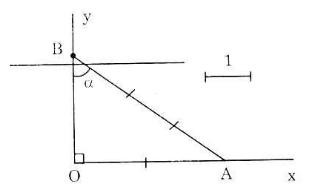
Vẽ góc vuông xOy. Trên tia Ox, lấy điểm A sao cho OA = 2cm. Lấy A làm tâm, vẽ cung tròn bán kính 3 cm sao cho cung tròn này cắt tia Oy tại B. Khi đó ∠OBA = α.
Thật vậy:
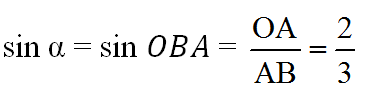
b)
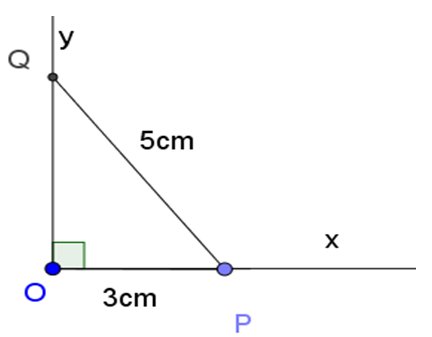
Vẽ góc vuông xOy. Trên tia Ox lấy điểm P sao cho OP = 3cm. Lấy P làm tâm, vẽ cung tròn bán kính 5 cm sao cho cung này cắt tia Oy tại Q. Khi đó ∠OPQ = α.
Thật vậy:
c)
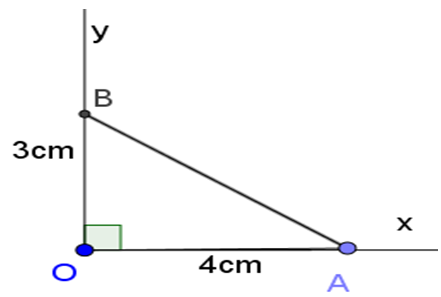
Vẽ góc vuông xOy. Trên tia Ox lấy điểm A sao cho OA = 4(cm). Trên tia Oy lấy điểm B sao cho OB = 3 cm. Khi đó ∠OAB = α.
Thật vậy:
d)
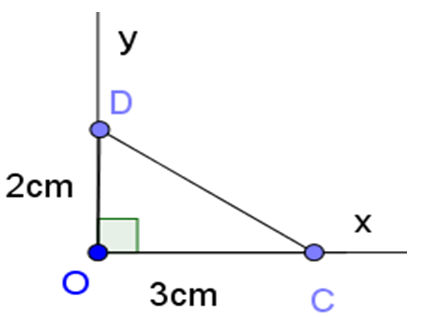
Vẽ góc vuông xOy. Trên tia Ox lấy điểm C sao cho OC = 3 cm. Trên tia Oy lấy D sao cho OD = 2 cm. Khi đó OCD = α.
Thật vậy:
Câu 2:
Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng. Với góc nhọn α tùy ý, ta có:
Gợi ý: Sử dụng định lí Pitago.
Xem đáp án
Lời giải:
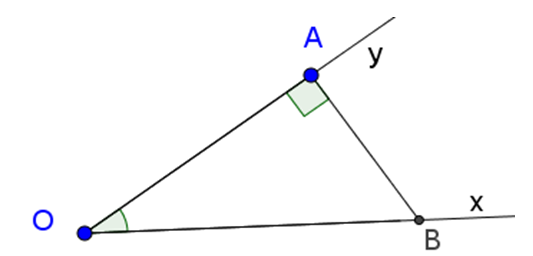
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
a) Ta có:
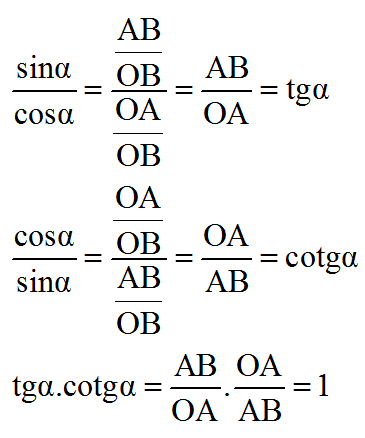
b) Áp dụng định lí pitago trong tam giác vuông OAB có:
OB2 = OA2 + AB2
Từ đó ta có:
Câu 3:
Cho tam giác ABC vuông tại A. Biết cosB = 0,8, hãy tính các tỉ số lượng giác của góc C.
Xem đáp án
Lời giải:
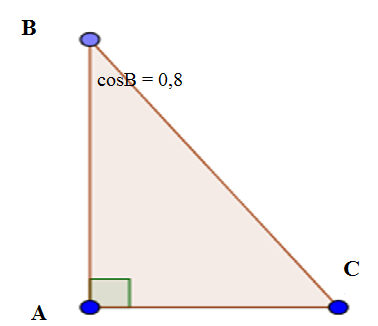
Ta có: ∠B + ∠C = 90o nên sinC = cosB = 0,8
Từ công thức sin2C + cos2C = 1 ta suy ra:
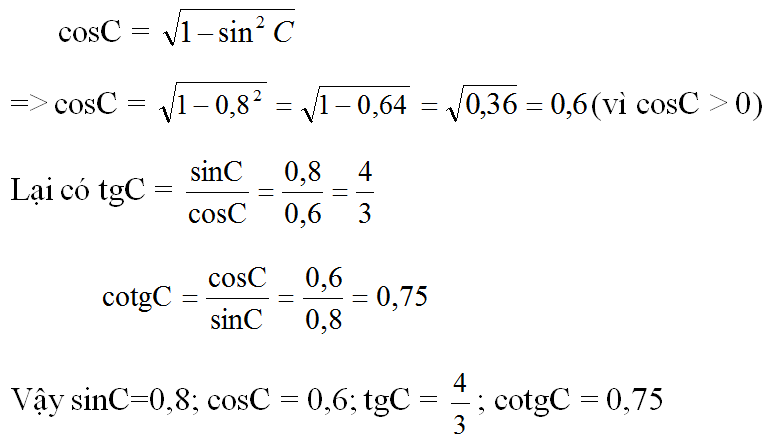
Câu 4:
Cho tam giác vuông có một góc 60o và cạnh huyền có độ dài là 8. Hãy tìm độ dài của cạnh đối diện với góc 60o.
Xem đáp án
Lời giải:
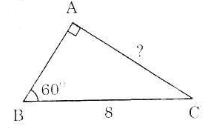
Giả sử ta có tam giác ABC như trên hình. Ta có:
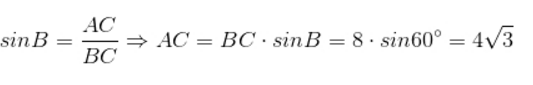
Câu 5:
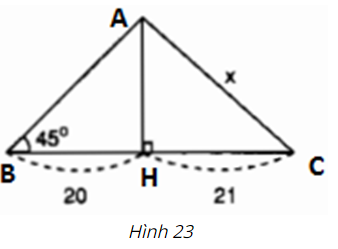
Bài 17 (trang 77 SGK Toán 9 Tập 1): Tìm x trong hình 23.
Xem đáp án
Lời giải:
Kí hiệu như hình trên.
Ta có tam giác ABH là vuông cân (vì ∠B = 45o) nên AH = 20.
Áp dụng định lí Pitago trong tam giác vuông AHC có:
x2 = AH2 + HC2 = 202 + 212 = 841
=> x = √841 = 29