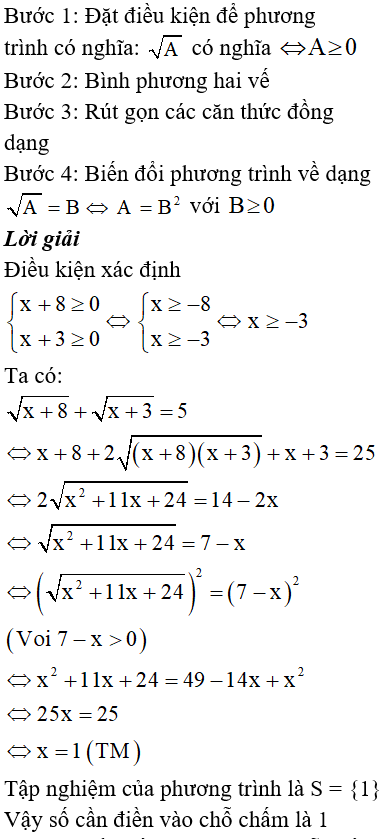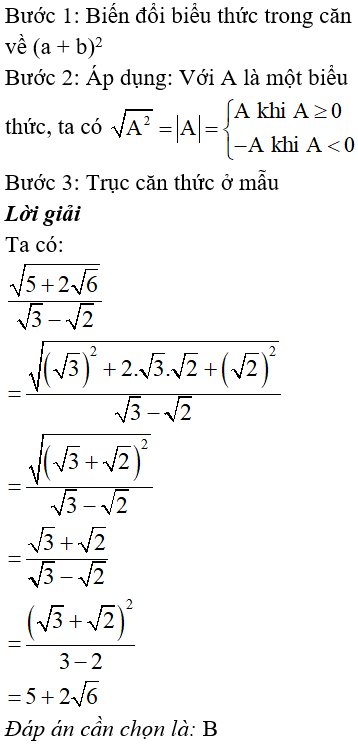10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Rút gọn biểu thức chứa căn bậc hai có đáp án (Vận dụng)

Câu 1:

Điền số thích hợp vào chỗ chấm

Giải phương trình $\sqrt{x + 8} + \sqrt{x + 3} = 5$

Tập nghiệm của phương trình là S = {…}

Câu 2:

Điền số thích hợp vào chỗ chấm

Rút gọn biểu thức $(\frac{1}{\sqrt{5} - \sqrt{2}} - \frac{1}{\sqrt{5} + \sqrt{2}} + 1) . \frac{1}{{(\sqrt{2} + 1)}^{2}} = ...$

Xem đáp án

Ta có:

$\begin{array}{l} (\frac{1}{\sqrt{5} - \sqrt{2}} - \frac{1}{\sqrt{5} + \sqrt{2}} + 1) . \frac{1}{{(\sqrt{2} + 1)}^{2}} \\ = (\frac{\sqrt{5} + \sqrt{2}}{5 - 2} - \frac{\sqrt{5} - \sqrt{2}}{5 - 2} + 1) . \frac{1}{{(\sqrt{2} + 1)}^{2}} \\ = (\frac{\sqrt{5} + \sqrt{2} - \sqrt{5} + \sqrt{2} + 3}{5 - 2}) . \frac{1}{{(\sqrt{2} + 1)}^{2}} \\ = \frac{3 + 2 \sqrt{2}}{3} . \frac{1}{3 + 2 \sqrt{2}} \\ = \frac{1}{3} \end{array}$

Vậy số cần điền vào chỗ chấm là $\frac{1}{3}$ .

Câu 3:

Lựa chọn đáp án đúng nhất:

Với x > 2. Rút gọn biểu thức $\sqrt{x + 3 + 2 \sqrt{x + 2}} - \sqrt{x + 6 - 4 \sqrt{x + 2}}$

A. $2 \sqrt{x + 2}$ .

B. $\sqrt{x + 2}$ .

C. 3.

D. 2.

Xem đáp án

Bước 1: Biến đổi biểu thức trong căn về ${(a \pm b)}^{2}$

Bước 2: Áp dụng: Quy tắc đưa thừa số ra ngoài dấu căn

Bước 3: Rút gọn biểu thức

Lời giải

Với x > 2, ta có:

$\begin{array}{l} \sqrt{x + 3 + 2 \sqrt{x + 2}} - \sqrt{x + 6 - 4 \sqrt{x + 2}} \\ = \sqrt{x + 2 + 2 \sqrt{x + 2} + 1} - \sqrt{x + 2 - 2.2. \sqrt{x + 2} + 2^{2}} \end{array}$

$\begin{array}{l} = \sqrt{{(\sqrt{x + 2} + 1)}^{2}} - \sqrt{{(\sqrt{x + 2} - 2)}^{2}} \\ = |\sqrt{x + 2} + 1| - |\sqrt{x + 2} - 2| \\ = \sqrt{x + 2} + 1 - \sqrt{x + 2} + 2 (V i x > 2 \Rightarrow \sqrt{x + 2} > \sqrt{4} \Leftrightarrow \sqrt{x + 2} > 2) \\ = 3 \end{array}$

Đáp án cần chọn là: C

Câu 4:

Lựa chọn đáp án đúng nhất:

Rút gọn biểu thức $\frac{\sqrt{5 + 2 \sqrt{6}}}{\sqrt{3} - \sqrt{2}}$ được kết quả là:

A. $2 + 5 \sqrt{6}$ .

B. $5 + 2 \sqrt{6}$ .

C. 5.

D. 2.

Xem đáp án

Câu 5:

Điền số thích hợp vào chỗ chấm

Rút gọn biểu thức $\sqrt{6 + 2 \sqrt{5} - \sqrt{29 - 12 \sqrt{5}}} = ...$

Xem đáp án

Bước 1: Biến đổi biểu thức trong căn về (a – b)²

Bước 2: Đưa thừa số ra ngoài dấu căn

Bước 3: Rút gọn biểu thức

Lời giải

Ta có:

$\begin{array}{l} \sqrt{6 + 2 \sqrt{5} - \sqrt{29 - 12 \sqrt{5}}} \\ = \sqrt{6 + 2 \sqrt{5} - \sqrt{{(2 \sqrt{5})}^{2} - 2.2. \sqrt{5} .3 + 3^{2}}} \\ = \sqrt{6 + 2 \sqrt{5} - \sqrt{{(2 \sqrt{5} - 3)}^{2}}} \\ = \sqrt{6 + 2 \sqrt{5} - 2 \sqrt{5} + 3} \\ = \sqrt{9} \\ = 3 \end{array}$

Đáp án cần chọn là: 3

Câu 6:

Hãy chọn đáp án đúng:

Cho biểu thức $A = \frac{2 \sqrt{x} - 9}{x - 5 \sqrt{x} + 6} - \frac{\sqrt{x} + 3}{\sqrt{x} - 2} - \frac{2 \sqrt{x} + 1}{3 - \sqrt{x}}$

Rút gọn A được kết quả là:

A. $\frac{\sqrt{x} - 1}{\sqrt{x} - 2}$ .

B. $\frac{\sqrt{x} + 1}{\sqrt{x} - 3}$ .

C. $\frac{\sqrt{x} - 1}{\sqrt{x} - 3}$ .

D. $\frac{\sqrt{x} + 1}{\sqrt{x} - 2}$ .

Xem đáp án

Bước 1: Xác định mẫu thức chung và quy đồng

Bước 2: Rút gọn tử thức

Bước 3: Rút gọn biểu thức

Lời giải

Điều kiện xác định: $x \geq 0; x \neq 4; x \neq 9$

Ta có:

$A = \frac{2 \sqrt{x} - 9}{x - 5 \sqrt{x} + 6} - \frac{\sqrt{x} + 3}{\sqrt{x} - 2} - \frac{2 \sqrt{x} + 1}{3 - \sqrt{x}}$

$\begin{array}{l} = \frac{2 \sqrt{x} - 9 - (\sqrt{x} + 3) (\sqrt{x} - 3) + (2 \sqrt{x} + 1) (\sqrt{x} - 2)}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{2 \sqrt{x} - 9 - x + 9 + 2 x - 3 \sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{x - \sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{x + \sqrt{x} - 2 \sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{\sqrt{x} (\sqrt{x} + 1) - 2 (\sqrt{x} + 1)}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{(\sqrt{x} - 2) (\sqrt{x} + 1)}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{\sqrt{x} + 1}{\sqrt{x} - 3} \end{array}$

Đáp án cần chọn là: B

Câu 7:

Điền số thích hợp vào chỗ chấm

Cho biểu thức $A = \frac{2 \sqrt{x} - 9}{x - 5 \sqrt{x} + 6} - \frac{\sqrt{x} + 3}{\sqrt{x} - 2} - \frac{2 \sqrt{x} + 1}{3 - \sqrt{x}}$

Với $x = \frac{2}{3 - \sqrt{5}}$ thì A = …

Xem đáp án

Bước 1: Tìm điều kiện để biểu thức A xác định và rút gọn A

Bước 2: Tính $\sqrt{x}$

Bước 3: Thay $\sqrt{x}$ vào biểu thức A đã rút gọn

Bước 4: Trục căn thức ở mẫu

Lời giải

Điều kiện xác định: $x \geq 0; x \neq 4; x \neq 9$

Ta có:

$A = \frac{2 \sqrt{x} - 9}{x - 5 \sqrt{x} + 6} - \frac{\sqrt{x} + 3}{\sqrt{x} - 2} - \frac{2 \sqrt{x} + 1}{3 - \sqrt{x}}$

$\begin{array}{l} = \frac{2 \sqrt{x} - 9 - (\sqrt{x} + 3) (\sqrt{x} - 3) + (2 \sqrt{x} + 1) (\sqrt{x} - 2)}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{2 \sqrt{x} - 9 - x + 9 + 2 x - 3 \sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{x - \sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{x + \sqrt{x} - 2 \sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{\sqrt{x} (\sqrt{x} + 1) - 2 (\sqrt{x} + 1)}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{(\sqrt{x} - 2) (\sqrt{x} + 1)}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{\sqrt{x} + 1}{\sqrt{x} - 3} \end{array}$

Ta lại có:

$\begin{array}{l} x = \frac{2}{3 - \sqrt{5}} = \frac{2 (3 + \sqrt{5})}{3^{2} - {(\sqrt{5})}^{2}} = \frac{6 + 2 \sqrt{5}}{4} = {(\frac{\sqrt{5} + 1}{2})}^{2} \\ \Rightarrow \sqrt{x} = \frac{\sqrt{5} + 1}{2} \end{array}$

Thay $\sqrt{x} = \frac{\sqrt{5} + 1}{2}$ vào biểu thức A đã rút gọn ta có:

$\begin{array}{l} A = (\frac{\sqrt{5} + 1}{2} + 1) : (\frac{\sqrt{5} + 1}{2} - 3) \\ = \frac{\sqrt{5} + 3}{2} : \frac{\sqrt{5} - 5}{2} \end{array}$

$\begin{array}{l} = \frac{\sqrt{5} + 3}{\sqrt{5} - 5} \\ = \frac{(\sqrt{5} + 3) (\sqrt{5} + 5)}{{(\sqrt{5})}^{2} - 5^{2}} \\ = \frac{20 + 8 \sqrt{5}}{- 20} \\ = - \frac{5 + 2 \sqrt{5}}{5} \approx - 1, 9 \end{array}$

Vậy số cần điền vào chỗ chấm là −1,9

Câu 8:

Điền số thích hợp vào chỗ chấm

Cho biểu thức $A = \frac{2 \sqrt{x} - 9}{x - 5 \sqrt{x} + 6} - \frac{\sqrt{x} + 3}{\sqrt{x} - 2} - \frac{2 \sqrt{x} + 1}{3 - \sqrt{x}}$

Giá trị nguyên lớn nhất của x để A < 1

Đáp số: x = …

Xem đáp án

Bước 1: Tìm điều kiện xác định của A và rút gọn biểu thức A

Bước 2: Xét hiệu A – 1 < 0

Bước 3: Kết hợp điều kiện tìm giá tri nguyên lớn nhất của x để A – 1 < 0

Lời giải

Điều kiện xác định: $x \geq 0; x \neq 4; x \neq 9$

Ta có:

$A = \frac{2 \sqrt{x} - 9}{x - 5 \sqrt{x} + 6} - \frac{\sqrt{x} + 3}{\sqrt{x} - 2} - \frac{2 \sqrt{x} + 1}{3 - \sqrt{x}}$

$\begin{array}{l} = \frac{2 \sqrt{x} - 9 - (\sqrt{x} + 3) (\sqrt{x} - 3) + (2 \sqrt{x} + 1) (\sqrt{x} - 2)}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{2 \sqrt{x} - 9 - x + 9 + 2 x - 3 \sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{x - \sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{x + \sqrt{x} - 2 \sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{\sqrt{x} (\sqrt{x} + 1) - 2 (\sqrt{x} + 1)}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{(\sqrt{x} - 2) (\sqrt{x} + 1)}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{\sqrt{x} + 1}{\sqrt{x} - 3} \end{array}$

$\begin{array}{l} A < 1 \Leftrightarrow \frac{\sqrt{x} + 1}{\sqrt{x} - 3} < 1 \\ \Leftrightarrow \frac{\sqrt{x} + 1}{\sqrt{x} - 3} - 1 < 0 \\ \Leftrightarrow \frac{4}{\sqrt{x} - 3} < 0 \\ \Leftrightarrow \sqrt{x} - 3 < 0 \\ \Leftrightarrow \sqrt{x} < 3 \\ \Leftrightarrow x < 9 \end{array}$

Kết hợp với điều kiện $x \geq 0; x \neq 4; x \neq 9$

Vậy A < 1 nếu $0 \leq x < 9; x \neq 4$

Vậy giá trị nguyên lớn nhất của x là 8.

Vậy số cần điền vào chỗ chấm là 8.

Câu 9:

Điền số thích hợp vào chỗ chấm

Cho biểu thức $A = \frac{2 \sqrt{x} - 9}{x - 5 \sqrt{x} + 6} - \frac{\sqrt{x} + 3}{\sqrt{x} - 2} - \frac{2 \sqrt{x} + 1}{3 - \sqrt{x}}$

Giá trị nguyên nhỏ nhất của x để $A \in ℤ$

Đáp số: x = …

Xem đáp án

$\begin{array}{l} = \frac{2 \sqrt{x} - 9 - (\sqrt{x} + 3) (\sqrt{x} - 3) + (2 \sqrt{x} + 1) (\sqrt{x} - 2)}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{2 \sqrt{x} - 9 - x + 9 + 2 x - 3 \sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{x - \sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{x + \sqrt{x} - 2 \sqrt{x} - 2}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{\sqrt{x} (\sqrt{x} + 1) - 2 (\sqrt{x} + 1)}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{(\sqrt{x} - 2) (\sqrt{x} + 1)}{(\sqrt{x} - 2) (\sqrt{x} - 3)} \\ = \frac{\sqrt{x} + 1}{\sqrt{x} - 3} \end{array}$

Câu 10:

$\frac{a + b}{b^{2}} \sqrt{\frac{a^{2} b^{4}}{a^{2} + 2 a b + b^{2}}}$ Hãy chọn đáp án đúng

Với a + b > 0 và b $\neq$ 0. Kết quả rút gọn của biểu thức là

A. 2a.

B. -a.

C. a.

D. |a|.

Xem đáp án

Với a + b > 0 và b $\neq$ 0, ta có:

$\begin{array}{l} \frac{a + b}{b^{2}} \sqrt{\frac{a^{2} b^{4}}{a^{2} + 2 a b + b^{2}}} \\ = \frac{a + b}{b^{2}} . \sqrt{\frac{{(a b^{2})}^{2}}{{(a + b)}^{2}}} \\ = \frac{a + b}{b^{2}} . |\frac{a b^{2}}{a + b}| \\ = \frac{a + b}{b^{2}} . \frac{|a| b^{2}}{a + b} = |a| (V i a + b > 0) \end{array}$

Đáp án cần chọn là: D

*Sai lầm cần tránh: Hàm số thường quên kiểm tra xem điều kiện của biểu thức đưa ra ngoài căn có dương không.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Rút gọn biểu thức chứa căn bậc hai có đáp án

Trắc nghiệm Rút gọn biểu thức chứa căn bậc hai có đáp án (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương