19 câu hỏi trắc nghiệm thuộc Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 11

Câu 1:

Chọn chữ cái trước đáp án đúng:

Đa thức $12 x - 36 - x^{2}$ bằng:

A. $- {(x + 6)}^{2}$

B.

${(- x - 6)}^{2}$

C.

${(- x + 6)}^{2}$

D.

$- {(x - 6)}^{2}$

Xem đáp án

Phương pháp:

Sử dụng công thức hằng đẳng thức.

Cách giải:

Đáp án D

$12 x - 36 - x^{2} = - (x^{2} - 12 x + 36) = - {(x - 6)}^{2}$

Câu 2:

Kết quả phép cộng

$\frac{3 x - 1}{3 x - 3} + \frac{- 2}{3 x - 3}$ là

A. $\frac{3 x + 1}{3 x - 3}$

B.

$\frac{x + 1}{x - 3}$

C.

$1$

D.

$\frac{3 x - 5}{3 (3 x - 3)}$

Xem đáp án

Phương pháp:

Quy đồng mẫu các phân thức sau đó tính tổng của hai phân thức.

Cách giải:

Đáp án C

Điều kiện: .

$\frac{3 x - 1}{3 x - 3} + \frac{- 2}{3 x - 3} = \frac{3 x - 1 - 2}{3 x - 3} = 1$

Câu 3:

Kết quả rút gọn biểu thức

$(x - 2 y) (x^{2} + 2 x y + 4 y^{2}) - (x + 2 y) (x^{2} - 2 x y + 4 y^{2})$ là:

A. $- 16 y^{3}$

B.

$- 4 y^{3}$

C.

$16 y^{3}$

D.

$- 12 y^{3}$

Xem đáp án

Phương pháp:Sử dụng hằng đẳng thức để rút gọn biểu thức.

Cách giải: Đáp án A

$(x - 2 y) (x^{2} + 2 x y + 4 y^{2}) - (x + 2 y) (x^{2} - 2 x y + 4 y^{2}) = x^{3} - {(2 y)}^{3} - [x^{3} + {(2 y)}^{3}]$

$= x^{3} - 8 y^{3} - x^{3} - 8 y^{3} = - 16 y^{3}$

Câu 4:

Số dư khi chia đa thức $3 x^{4} - 2 x^{3} + x^{2} - 2 x + 2$ cho đa thức $x - 2$ là:

A. 50

B. 34

C. 32

D. 30

Xem đáp án

Phương pháp:Chia đa thức bài cho đa thức $x - 2$ hoặc biến đổi biểu thức đã cho theo biểu thức $x - 2$ để tìm số dư của phép chia.

Cách giải:

Đáp án B

$3 x^{4} - 2 x^{3} + x^{2} - 2 x + 2 = 3 x^{4} - 6 x^{3} + 4 x^{3} - 8 x^{2} + 9 x^{2} - 18 x + 16 x - 32 + 34$

$= 3 x^{2} (x - 2) + 4 x^{2} (x - 2) + 9 x (x - 2) + 16 (x - 2) + 34$

$= (x - 2) (3 x^{3} + 4 x^{2} + 9 x + 16) + 34$

Vậy đa thức $3 x^{4} - 2 x^{3} + x^{2} - 2 x + 2$ chia cho đa thức $x - 2$ được $3 x^{3} + 4 x^{2} + 9 x + 16$ và dư 34.

Câu 5:

Hình vuông có độ dài đường chéo là 6cm. Độ dài cạnh hình vuông đó là:

A. $\sqrt{18} c m$

B.

$18 c m$

C. 3cm

D. 4 cm

Xem đáp án

Phương pháp:Độ dài đường chéo của hình vuông cạnh a là $a \sqrt{2}$ .

Cách giải:

Đáp án A

Độ dài cạnh hình vuông là $\frac{6}{\sqrt{2}} = 3 \sqrt{2} (c m)$ .

Câu 6:

Một hình chữ nhật có diện tích $15 c m^{2}$ . Nếu tăng chiều dài lên hai lần, chiều rộng lên ba lần thì diện tích của hình chữ nhật mới là:

A. $30 c m^{2}$

B.

$45 c m^{2}$

C.

$90 c m^{2}$

D.

$75 c m^{2}$

Xem đáp án

Phương pháp:

Công thức tính diện tích hình chữ nhật là: $S = a b$ .

Cách giải:

Đáp án C

Nếu tăng chiều dài lên hai lần, chiều rộng lên ba lần thì diện tích của hình chữ nhật mới sẽ tăng lên: $2.3 = 6$ lần $\Rightarrow$ diện tích hình chữ nhật mới là: $15.6 = 90 (c m^{2})$ .

Câu 7:

Cho hình thang cân $A B C D (A B / / C D)$ có $A = 135 °$ thì góc C bằng:

A. $35 °$

B.

$45 °$

C.

$55 °$

D. Không tính được

Xem đáp án

Phương pháp:

Sử dụng tính chất của hình thang.

Cách giải:

Đáp án B

Vì $A B C D (A B / / C D) \Rightarrow ∠ A + ∠ D = 180 °$ (hai góc trong cùng phía)

Mà ABCD là hình thang cân $\Rightarrow ∠ C = ∠ D$

$\Rightarrow ∠ C = 180 ° - ∠ A = 180 ° - 13 ° = 45 °$

Câu 8:

Tứ giác có các đỉnh là trung điểm các cạnh của một tứ giác có hai đường chéo bằng nhau là:

A. Hình thang cân

B. Hình chữ nhật

C. Hình thoi

D. Hình vuông

Xem đáp án

Phương pháp:

Vẽ hình, sử dụng dấu hiện nhận biết các hình để chọn đáp án đúng.

Cách giải:

Đáp án C

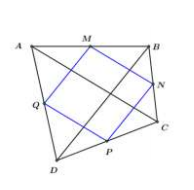
Giả sử tứ giác ABCD có hai đường chéo AC=BD.

Gọi $M, N, P, Q$ lần lượt là trung điểm của các cạnh $A B, B C, C D, D A$ .

Xét $Δ A B D$ ta có:

$M, Q$ lần lượt là trung điểm của

$A B, A D$

$\Rightarrow M Q$ là đường trung bình của $Δ A B D$

$\Rightarrow \{\begin{cases} M Q / / B D \\ M Q = \frac{1}{2} B D \end{cases}$ $(1)$

Xét $Δ B C D$ ta có:

N, P lần lượt là trung điểm của BC, CD

NP là đường trung bình của

$\Rightarrow \{\begin{cases} N P / / B D \\ N P = \frac{1}{2} B D \end{cases}$ $(2)$

Từ (1) và (2) $\Rightarrow \{\begin{cases} M Q = N P (= \frac{1}{2} B D) \\ M Q / / N P (/ / B D) \end{cases} \Rightarrow M N P Q$ là hình bình hành (dhnb).

Xét $Δ A B C$ ta có:

M,N lần lượt là trung điểm của AB, BC

MN là đường trung bình của $Δ A B C$

$\Rightarrow \{\begin{cases} M N / / A C \\ M N = \frac{1}{2} A C \end{cases}$

Mà $A C = B D (g t) \Rightarrow M N = M Q$

$\Rightarrow M N P Q$ là hình thoi. (dhnb).

Câu 9:

Phân tích đa thức sau thành nhân tử: $6 x y + 12 x - 4 y - 8$

Xem đáp án

Phương pháp:

Sử dụng các phương pháp nhóm hạng tử, đặt nhân tử chung, hằng đẳng thức…

Cách giải:

$6 x y + 12 x - 4 y - 8$

$= 6 x (y + 2) - 4 (y + 2)$

$= 2 (3 x - 2) (y + 2)$

Câu 10:

Phân tích đa thức sau thành nhân tử:

$x^{3} + 2 x^{2} - x - 2$

Xem đáp án

Phương pháp:

Sử dụng các phương pháp nhóm hạng tử, đặt nhân tử chung, hằng đẳng thức…

Cách giải:

$x^{3} + 2 x^{2} - x - 2$

$= x^{2} (x + 2) - (x + 2)$

$= (x^{2} - 1) (x + 2)$

$= (x - 1) (x + 1) (x + 2)$

Câu 11:

Chứng minh rằng giá trị biểu thức sau không phụ thuộc vào giá trị của biến:

${(x - 2)}^{2} - (x - 1) (x + 1) + 4 (x + 2)$

Xem đáp án

Phương pháp:

Dùng các phép biến đổi cơ bản.

Cách giải:

${(x - 2)}^{2} - (x - 1) (x + 1) + 4 (x + 2)$

$= x^{2} - 4 x + 4 - (x^{2} - 1) + 4 x + 8$

$= 13$

Vậy giá trị biểu thức không phụ thuộc vào biến.

Câu 12:

Tìm x, biết $(2 - x) (2 + x) = 3$

Xem đáp án

Phương pháp:

Dùng các phép biến đổi cơ bản.

Cách giải:

$(2 - x) (2 + x) = 3$

$\Leftrightarrow 4 - x^{2} = 3$

$\Leftrightarrow x^{2} = 1 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 1 \end{array}$

Vậy $x = - 1$ hoặc $x = 1$ .

Câu 13:

Thực hiện phép tính: $\frac{x + 2}{x - 3} - \frac{x^{2} + 6}{x^{2} - 3 x}$

Xem đáp án

Phương pháp:

Tìm điều kiện xác định sau đó dùng các quy tắc cộng, trừ, rút gọn phân thức để giải toán.

Cách giải:

$\frac{x + 2}{x - 3} - \frac{x^{2} + 6}{x^{2} - 3 x} (x \neq 0; x \neq 3)$

$= \frac{x + 2}{x - 3} - \frac{x^{2} + 6}{x (x - 3)} = \frac{x (x + 2) - x^{2} - 6}{x (x - 3)}$

$\begin{array}{l} = \frac{x^{2} + 2 x - x^{2} - 6}{x (x - 3)} = \frac{2 x - 6}{x (x - 3)} \\ = \frac{2 (x - 3)}{x (x - 3)} = \frac{2}{x} \end{array}$

Câu 14:

Thực hiện phép tính:

$\frac{4 x - 4}{x^{2} - 4 x + 4} : \frac{x^{2} - 1}{{(2 - x)}^{2}}$

Xem đáp án

Phương pháp:

Tìm điều kiện xác định sau đó dùng các quy tắc cộng, trừ, rút gọn phân thức để giải toán.

Cách giải:

$\frac{4 x - 4}{x^{2} - 4 x + 4} : \frac{x^{2} - 1}{{(2 - x)}^{2}} (x \neq 2, x \neq \pm 1)$

$= \frac{4 (x - 1)}{{(x - 2)}^{2}} . \frac{{(2 - x)}^{2}}{x^{2} - 1}$

$= \frac{4 (x - 1)}{{(x - 2)}^{2}} . \frac{{(x - 2)}^{2}}{(x - 1) (x + 1)}$

$= \frac{4}{x + 1}$

Câu 15:

Cho tam giác ABC có AD là phân giác của góc $B A C (D \in B C)$ . Từ D kẻ các đường thẳng song song với AB và AC, chúng cắt AC,AB tại E và E.

Chứng minh: Tứ giác AEDF là hình thoi.

Xem đáp án

Phương pháp:

Dùng dấu hiệu nhận biết hình

Cách giải:

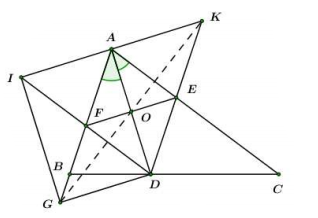
Xét tứ giác AEDF ta có:

$D E / / F A, D F / / E A (g t)$

$\Rightarrow A E D F$ nên là hình bình hành (dhnb).

Lại có AD là phân giác của $∠ F A E (g t) \Rightarrow A E D F$ là hình thoi (dhnb). (đpcm)

Câu 16:

Cho tam giác ABC có AD là phân giác của góc $B A C (D \in B C)$ . Từ kẻ các đường thẳng song song với AB và AC, chúng cắt AC, AB tại E và F.

Trên tia AB lấy điểm G sao cho F là trung điểm của AG. Chứng minh tứ giác EFGD là hình bình hành.

Xem đáp án

Phương pháp:

Dùng dấu hiệu nhận biết hình bình hành.

Cách giải:

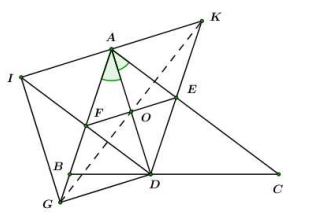
Ta có: AEDF là hình thoi (cmt)

$\Rightarrow \{\begin{cases} D E / / A F \\ D E = A F \end{cases}$ (tính chất)

Xét tứ giác DEFG có : $D E = G F (= F A), D E / / G F$

$\Rightarrow D E F G$ là hình bình hành (dhnb).

Câu 17:

Cho tam giác ABC có AD là phân giác của góc $B A C (D \in B C)$ . Từ kẻ các đường thẳng song song với AB và AC, chúng cắt AC,AB tại E và F.

Gọi I là điểm đối xứng của D qua F, tia IA cắt tia DE tại K. Gọi O là giao điểm của AD và EF. Chứng minh G đối xứng với K qua O.

Xem đáp án

Phương pháp:

Dùng tính chất của hình bình hành, hình thoi để giải quyết bài toán.

Cách giải:

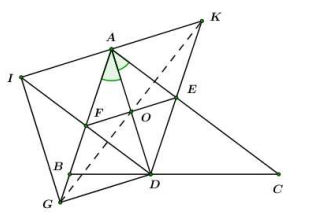
Vì $F A = F G (g t), F I = F D (g t)$ nên IADG là hình bình hành (dhnb)

$\Rightarrow I A / / D G$ (tính chất) hay $A K / / D G$ .

Lại có $D K / / G A$ (do $D E / / A B$ )

$\Rightarrow A K D G$ là hình bình hành (dhnb)

Mà O là trung điểm của AD nên O cũng là trung điểm của GK. (hai đường chéo hình hình hành cắt nhau tại trung điểm của mỗi đường).

Vậy K đối xứng với G qua O. (đpcm).

Câu 18:

Cho tam giác ABC có AD là phân giác của góc

$B A C (D \in B C)$ . Từ kẻ các đường thẳng song song với AB và AC, chúng cắt AC,AB tại E và F.

Tìm điều kiện của tam giác ABC để tứ giác ADGI là hình vuông.

Xem đáp án

Phương pháp:

Dùng dấu hiệu nhận biết của hình vuông.

Cách giải:

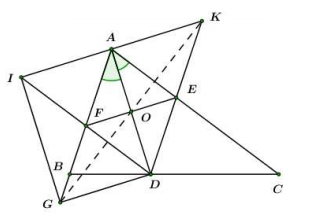
Tứ giác IADG là hình bình hành (cmt).

Ta có: AEDF là hình thoi $\Rightarrow A D ⊥ E F .$

Mà EFGD là hình bình hành $\Rightarrow D G / / E F$ .

$\Rightarrow A D ⊥ G D$ (từ vuông góc đến song song).

$\Rightarrow I A D G$ là hình chữ nhật.

$\Rightarrow I A D G$ là hình vuông $\Leftrightarrow A G ⊥ D I \Leftrightarrow A G ⊥ C A$ (Vì $D I / / C A$ )

$\Leftrightarrow Δ A B C$ vuông tại A

Vậy $Δ A B C$ vuông tại A thì IADG là hình vuông.

Câu 19:

Tính giá trị của biểu thức: $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) ... (1 - \frac{1}{2017^{2}})$

Xem đáp án

Phương pháp:

Sử dụng hằng đẳng thức, biến đổi và rút gọn biểu thức.

Cách giải:

Ta có:

$\begin{array}{l} (1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) ... (1 - \frac{1}{2017^{2}}) \\ = (1 - \frac{1}{2}) (1 + \frac{1}{2}) (1 - \frac{1}{3}) (1 + \frac{1}{3}) ... (1 - \frac{1}{2017}) (1 + \frac{1}{2017}) \\ = (1 - \frac{1}{2}) (1 - \frac{1}{3}) ... (1 - \frac{1}{2017}) . (1 + \frac{1}{2}) (1 + \frac{1}{3}) ... (1 + \frac{1}{2017}) \\ = (\frac{1}{2} . \frac{2}{3} .... \frac{2016}{2017}) . (\frac{3}{2} . \frac{4}{3} .... \frac{2018}{2017}) \\ = \frac{1}{2017} . \frac{2018}{2} \\ = \frac{1009}{2017} . \end{array}$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bộ 14 đề thi Học kì 1 Toán 8 có đáp án

Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 11

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương