Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 1
-
3193 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Phân tích các đa thức sau thành nhân tử: .
 Xem đáp án
Xem đáp án
Phương pháp:
Nhóm hạng tử, đặt hạng tử chung, hằng đẳng thức...
Cách giải:
.
Câu 2:
Tính nhanh giá trị của biểu thức: với .
 Xem đáp án
Xem đáp án
Phương pháp:
Nhóm hạng tử, đặt hạng tử chung, hằng đẳng thức...
Cách giải:
.
Thay vào biểu thức ta được:
.
Câu 3:
Tìm x biết: .
 Xem đáp án
Xem đáp án
Phương pháp:
Phân tích đa thức thành nhân tử, sử dụng tính chất của phép chia hết.
Cách giải:
Vậy hoặc .
Câu 4:
 Xem đáp án
Xem đáp án
Phương pháp:
Phân tích đa thức thành nhân tử, sử dụng tính chất của phép chia hết.
Cách giải:
Để đa thức B chia hết cho đa thức thì .
Vậy .
Câu 5:
Cho biểu thức với .
Chứng tỏ rằng .
 Xem đáp án
Xem đáp án
Phương pháp:
Áp dụng linh hoạt các kĩ năng để rút gọn biểu thức, sau đó tính giá trị biểu thức.
Phần c sử dụng phương pháp ước số
Cách giải:
với
với .
Vậy ta có điều phải chứng minh.
Câu 6:
Cho biểu thức với .
Tính giá trị của biểu thức P, với x thỏa mãn .
 Xem đáp án
Xem đáp án
Phương pháp:
Áp dụng linh hoạt các kĩ năng để rút gọn biểu thức, sau đó tính giá trị biểu thức.
Phần c sử dụng phương pháp ước số
Cách giải:
với .
Tính giá trị của biểu thức P, với x thỏa mãn .
Điều kiện: .
Ta có:
Thay thì .
Câu 7:
Cho biểu thức với .
 Xem đáp án
Xem đáp án
Phương pháp:
Áp dụng linh hoạt các kĩ năng để rút gọn biểu thức, sau đó tính giá trị biểu thức.
Phần c sử dụng phương pháp ước số
Cách giải:
với .
Tìm giá trị nguyên của x để biểu thức P có giá trị nguyên.
Điều kiện: .
Ta có: hay
Mà . Ta có bảng giá trị:
|
|
-3 |
-1 |
1 |
3 |
|
|
-8 |
-6 |
-4 (loại) |
-2 |
Vậy thì P nhận giá trị nguyên.
Câu 8:
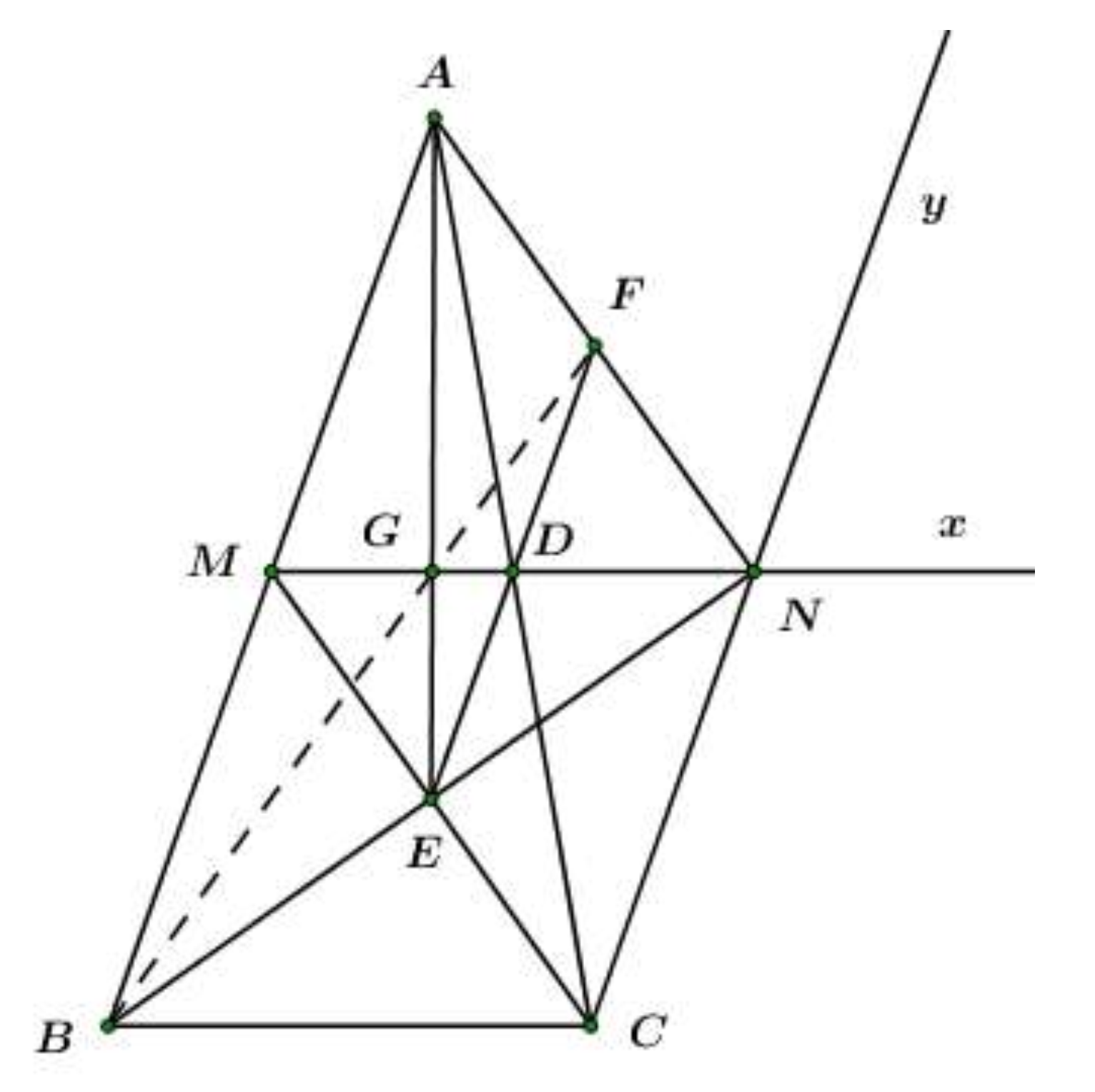
Cho tam giác ABC có , từ trung điểm M của AB kẻ tia Mx song song BC, từ C kẻ tia Cy song song AB sao cho Mx cắt Cy tại N.
Chứng minh tứ giác MBCN là hình bình hành.
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng dấu hiệu nhận biết và tính chất của hình bình hành, dấu hiệu nhận biết tam giác vuông, chứng minh tam giác bằng nhau và tính chất trọng tâm của tam giác.
Cách giải:
Tứ giác BMNC có:, nên MNBC là hình bình hành. (dhnb)
Câu 9:
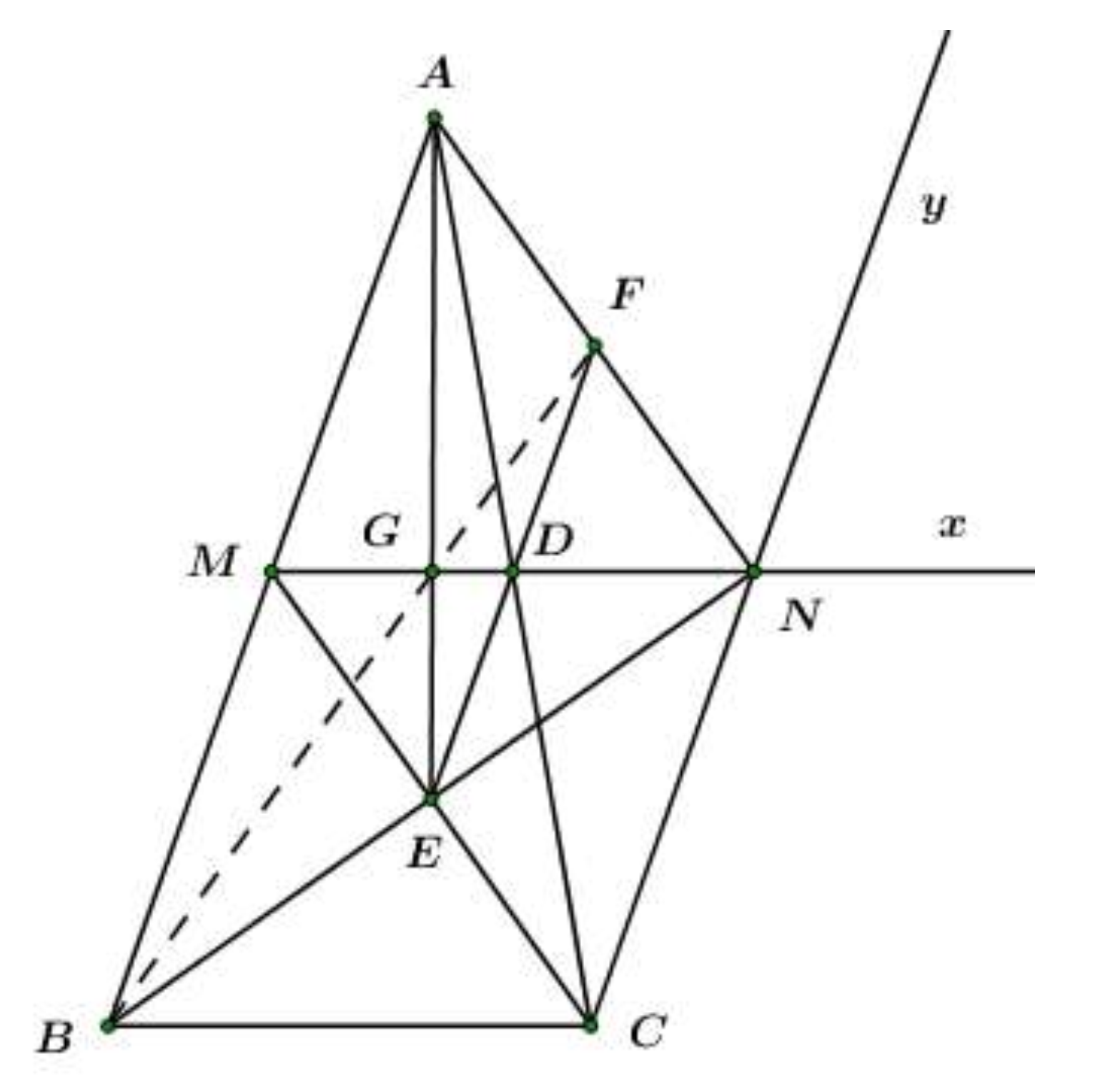
Cho tam giác ABC có , từ trung điểm M của AB kẻ tia Mx song song BC, từ C kẻ tia Cy song song AB sao cho Mx cắt Cy tại N.
Chứng minh .
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng dấu hiệu nhận biết và tính chất của hình bình hành, dấu hiệu nhận biết tam giác vuông, chứng minh tam giác bằng nhau và tính chất trọng tâm của tam giác.
Cách giải:
Vì BMNC là hình bình hành (cmt) nên .
Lại có: .
Tam giác có đường trung tuyến NM bằng nửa cạnh đối AB nên tam giác ABN vuông tại N, hay AN vuông góc với BN (đpcm).
Câu 10:
Cho tam giác ABC có , từ trung điểm M của AB kẻ tia Mx song song BC, từ C kẻ tia Cy song song AB sao cho Mx cắt Cy tại N.
Gọi D là giao điểm của MN với AC, E là giao điểm của MC với BN, F là giao điểm của ED với AN. Chứng minh .
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng dấu hiệu nhận biết và tính chất của hình bình hành, dấu hiệu nhận biết tam giác vuông, chứng minh tam giác bằng nhau và tính chất trọng tâm của tam giác.
Cách giải:
Tứ giác AMCN có
là hình bình hành (dhnb)
. (tính chất)
Xét có:
M là trung điểm của AB
là trung điểm của AC (định lý đảo).
Xét và có:
(cmt)
(hai góc đối đỉnh)
(hai góc so le trong)
(g – c – g) (đpcm).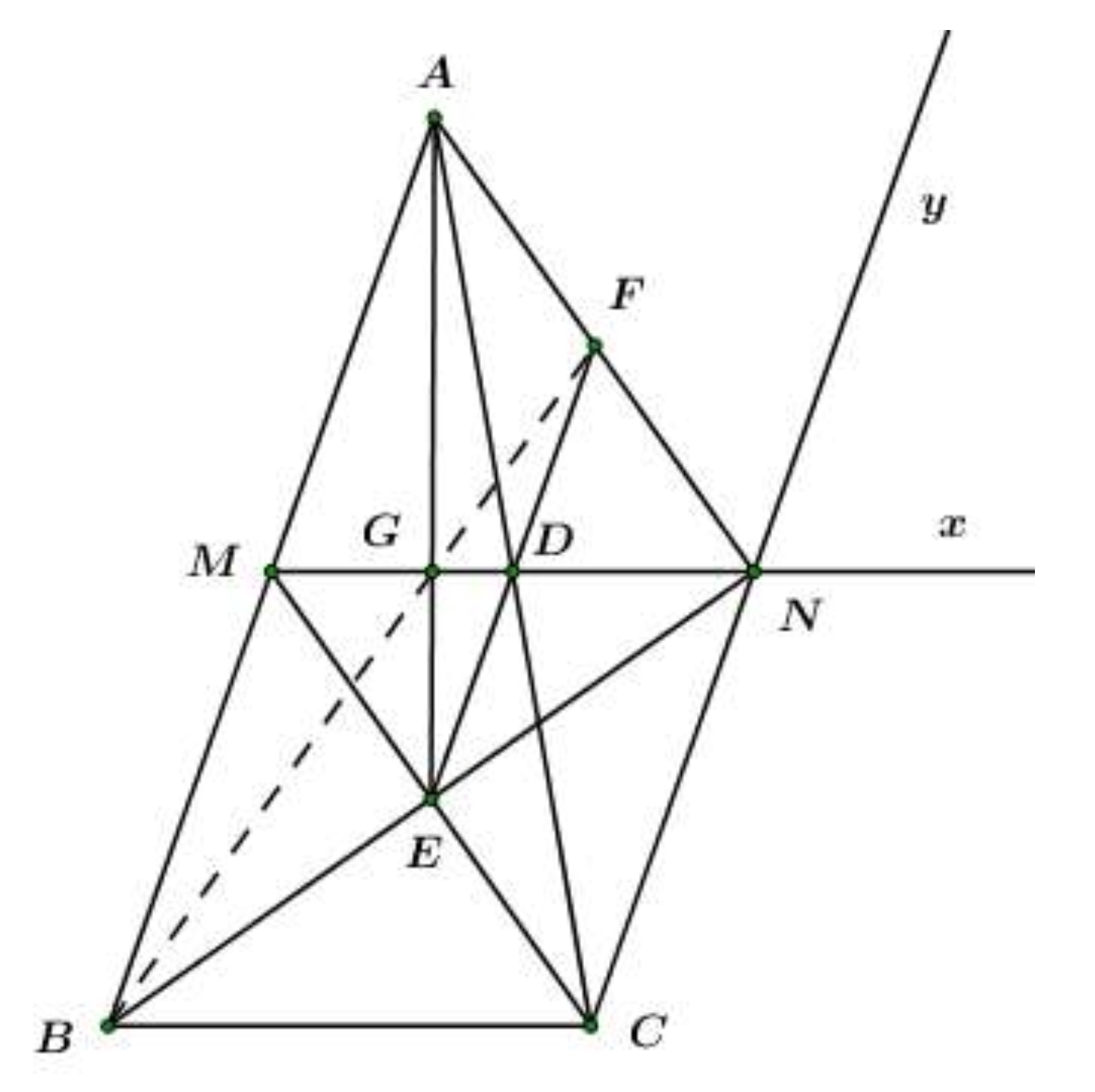
Câu 11:
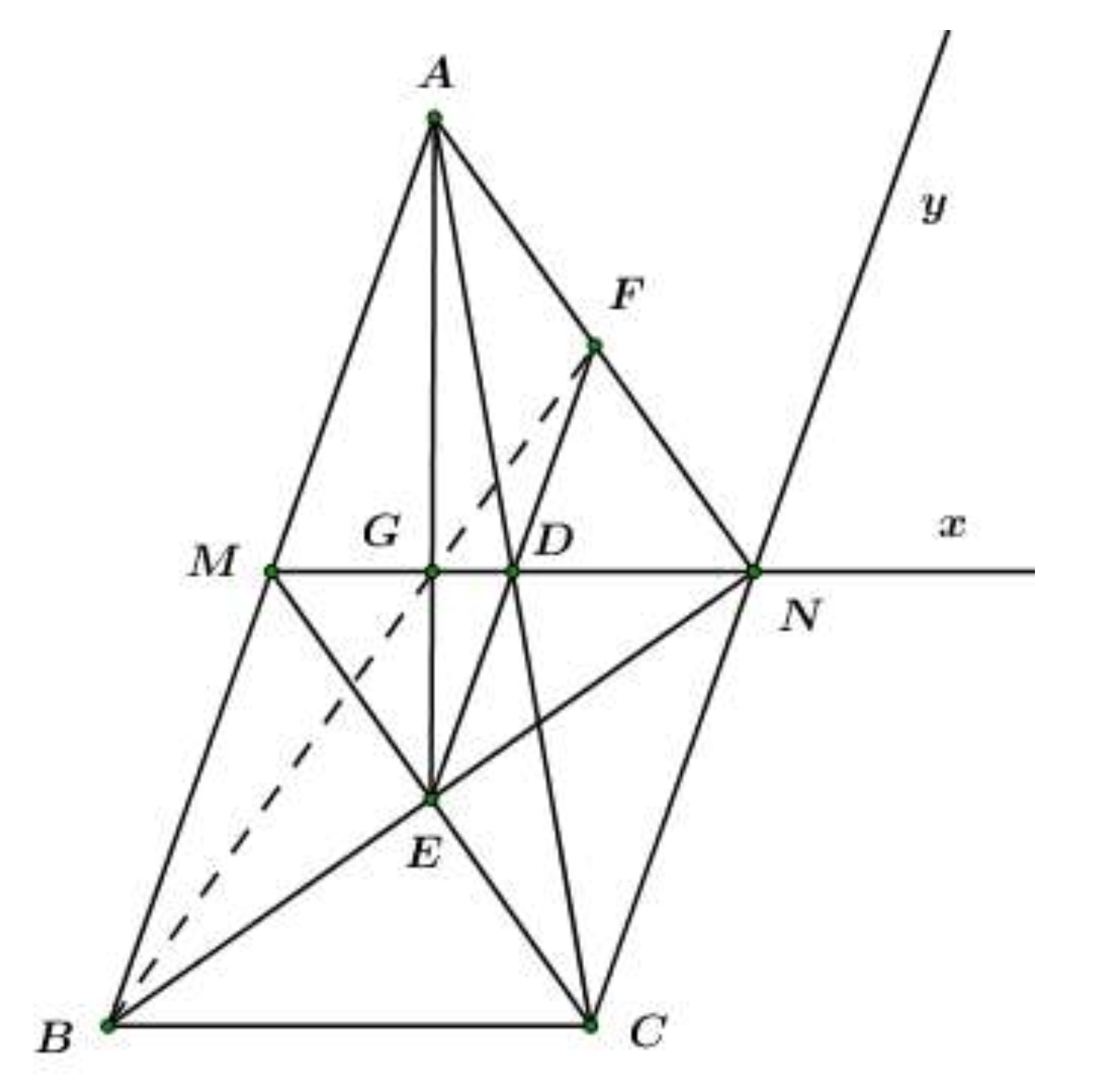
Cho tam giác ABC có , từ trung điểm M của AB kẻ tia Mx song song BC, từ C kẻ tia Cy song song AB sao cho Mx cắt Cy tại N.
Gọi G là giao điểm của AE với MN. Chứng minh B, G, F thẳng hàng.
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng dấu hiệu nhận biết và tính chất của hình bình hành, dấu hiệu nhận biết tam giác vuông, chứng minh tam giác bằng nhau và tính chất trọng tâm của tam giác.
Cách giải:
Ta có: (cmt) .
Mà (AMCN là hình bình hành) và .
Vậy F là trung điểm AN.
Xét tam giác ABN có G là giao của hai đường trung tuyến AE và NM nên G là trọng tâm của tam giác ABN.
BG đi qua trung điểm F của AN B, G, F thẳng hàng.
Câu 12:
Cho các số x, y, z dương thỏa mãn .
Tìm giá trị nhỏ nhất của biểu thức .
 Xem đáp án
Xem đáp án
Phương pháp:
Áp dụng bất đẳng thức Cauchy cho hai số dương ta có:
Cộng theo vế ba bất đẳng thức trên ta được:
Dấu “=” xảy ra .
Vậy giá trị nhỏ nhất của M là khi .
