12 câu hỏi trắc nghiệm thuộc Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 9

Câu 1:

Thực hiện các phép tính: $2 x^{2} (3 x^{2} - 2 x + 5)$

Xem đáp án

Phương pháp:

Tìm điều kiện xác định và thực hiện các phép toán cơ bản.

Cách giải:

Thực hiện các phép tính.

$2 x^{2} (3 x^{2} - 2 x + 5) = 6 x^{4} - 4 x^{3} + 10 x^{2}$ .

Câu 2:

Thực hiện các phép tính: $\frac{x}{x^{2} - 1} - \frac{1}{x^{2} - 1}$

Xem đáp án

Phương pháp:

Tìm điều kiện xác định và thực hiện các phép toán cơ bản.

Cách giải:

Thực hiện các phép tính.

$\frac{x}{x^{2} - 1} - \frac{1}{x^{2} - 1}$

Điều kiện: $x^{2} - 1 \neq 0 \Leftrightarrow x \neq \pm 1$ .

$\frac{x}{x^{2} - 1} - \frac{1}{x^{2} - 1} = \frac{x - 1}{(x - 1) (x + 1)} = \frac{1}{x + 1}$

Câu 3:

Tính số đo các góc của hình bình hành ABCD biết

∠ A + ∠ B + ∠ C = 330^{o}

.

Xem đáp án

Phương pháp: Sử dụng định lý về tổng bốn góc trong một tứ giác và tính chất hình bình hành.

Cách giải:

Ta có: $∠ A + ∠ B + ∠ C = 330^{o}$ mà $∠ A + ∠ B + ∠ C + ∠ D = 360^{o}$ (tổng các góc trong tứ giác)

$\Rightarrow ∠ D = 360^{o} - (∠ A + ∠ B + ∠ C) = 360^{o} - 330^{o} = 30^{o}$

Lại có ABCD là hình bình hành $\Rightarrow ∠ D = ∠ B = 30^{o}$ (hai góc đối trong hình bình hành)

\Rightarrow ∠ A = ∠ C = \frac{360^{o} - 2 ∠ B}{2} = \frac{360^{o} - {2.30}^{o}}{2} = 150^{o}

Câu 4:

Phân tích đa thức

x^{2} - 2 x y

thành nhân tử.

Xem đáp án

Phương pháp:

Phân tích đa thức thành nhân tử, sử dụng tính chất của phép chia hết.

Cách giải:

Phân tích đa thức thành nhân tử.

$x^{2} - 2 x y = x (x - 2 y)$ .

Câu 5:

Tìm x biết $x^{2} - 4 - 2 (x + 2) = 0$ .

Xem đáp án

Phương pháp:

Phân tích đa thức thành nhân tử, sử dụng tính chất của phép chia hết.

Cách giải:

$x^{2} - 4 - 2 (x + 2) = 0$

$\Leftrightarrow (x - 2) (x + 2) - 2 (x + 2) = 0$

$\Leftrightarrow (x + 2) (x - 4) = 0$

$\Leftrightarrow [\begin{array}{l} x + 2 = 0 \\ x - 4 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - 2 \\ x = 4 \end{array}$

Vậy $x = - 2$ hoặc $x = 4$ .

Câu 6:

Tìm m sao cho đa thức

2 x^{3} - 5 x^{2} + 6 x + m

chia hết cho đa thức

2 x - 5

.

Xem đáp án

Phương pháp:

Phân tích đa thức thành nhân tử, sử dụng tính chất của phép chia hết.

Cách giải:

$2 x^{3} - 5 x^{2} + 6 x + m = 2 x^{3} - 5 x^{2} + 6 x - 15 + 15 + m$

$= x^{2} (2 x - 5) + 3 (2 x - 5) + 15 + m$

Để đa thức $2 x^{3} - 5 x^{2} + 6 x + m$ chia hết cho đa thức $2 x - 5$ thì $15 + m = 0 \Leftrightarrow m = - 15$ .

Vậy m= -15.

Câu 7:

Cho biểu thức $A = \frac{4}{x + 2} + \frac{2}{x - 2} - \frac{5 x - 6}{x^{2} - 4}$ $(x \neq \pm 2)$

Rút gọn rồi tính giá trị biểu thức A khi $x = \frac{7}{3}$

Xem đáp án

Phương pháp:

Tìm điều kiện xác định. Áp dụng linh hoạt các kĩ năng để rút gọn biểu thức, sau đó tính giá trị biểu thức.

Cách giải:

Điều kiện: $x \neq \pm 2$ .

$A = \frac{4}{x + 2} + \frac{2}{x - 2} - \frac{5 x - 6}{x^{2} - 4} = \frac{4 (x - 2) + 2 (x + 2) - (5 x - 6)}{(x + 2) (x - 2)}$

$= \frac{x + 2}{(x + 2) (x - 2)} = \frac{1}{x - 2}$

Thay $x = \frac{7}{3}$ vào biểu thức ta được: $A = \frac{1}{x - 2} = \frac{1}{\frac{7}{3} - 2} = 3$

Vậy với $x = \frac{7}{3}$ thì $A = 3$ .

Câu 8:

Cho biểu thức $A = \frac{4}{x + 2} + \frac{2}{x - 2} - \frac{5 x - 6}{x^{2} - 4}$ $(x \neq \pm 2)$

Tìm giá trị của $x \neq 0$ để $A . \frac{1}{x} = - 1$ .

Xem đáp án

Phương pháp:

Tìm điều kiện xác định. Áp dụng linh hoạt các kĩ năng để rút gọn biểu thức, sau đó tính giá trị biểu thức.

Cách giải:

Điều kiện $x \neq 0; x \neq \pm 2$

A . \frac{1}{x} = - 1 \Leftrightarrow \frac{1}{x - 2} . \frac{1}{x} = - 1

\Leftrightarrow - (x^{2} - 2 x) = 1 \Leftrightarrow x^{2} + 2 x + 1 = 0

\Leftrightarrow {(x - 1)}^{2} = 0 \Leftrightarrow x - 1 = 0 \Leftrightarrow x = 1

(tm)

Vậy $x = 1$

Câu 9:

Cho tam giác ABC vuông tại $(A B < A C)$ , đường cao AH. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC.

Chứng minh tứ giác AMPN là hình chữ nhật.

Xem đáp án

Phương pháp:

Sử dụng dấu hiệu nhận biết và tính chất của hình bình hành, hình chữ nhật, hình thang cân và công thức tính diện tích tam giác.

Cách giải:

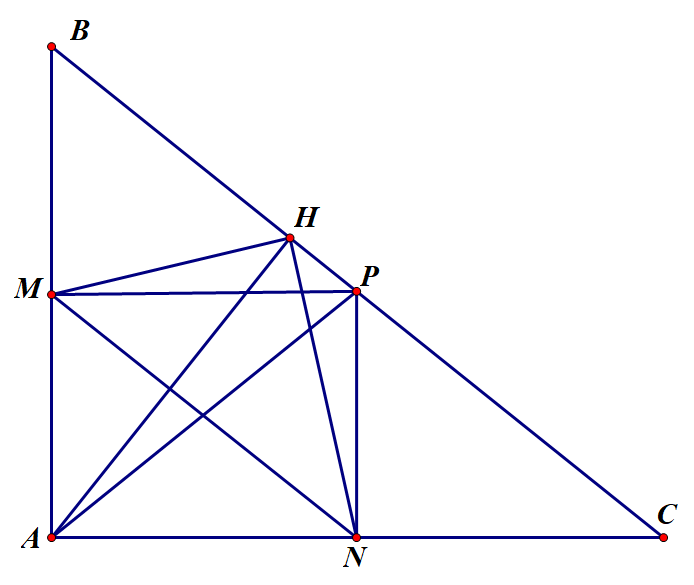
Vì M là trung điểm AB, P là trung điểm BC nên MP là đường trung bình của tam giác ABC .

$\Rightarrow M P // A C$

Tương tự ta có $N P // A B \Rightarrow A M P N$ là hình bình hành. Lại có $∠ M A N = 90^{o}$ nên AMPN là hình chữ nhật.

Câu 10:

Cho tam giác ABC vuông tại $(A B < A C)$ , đường cao AH. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC.

Chứng minh tứ giác MNPH là hình thang cân.

Xem đáp án

Phương pháp:

Sử dụng dấu hiệu nhận biết và tính chất của hình bình hành, hình chữ nhật, hình thang cân và công thức tính diện tích tam giác.

Cách giải:

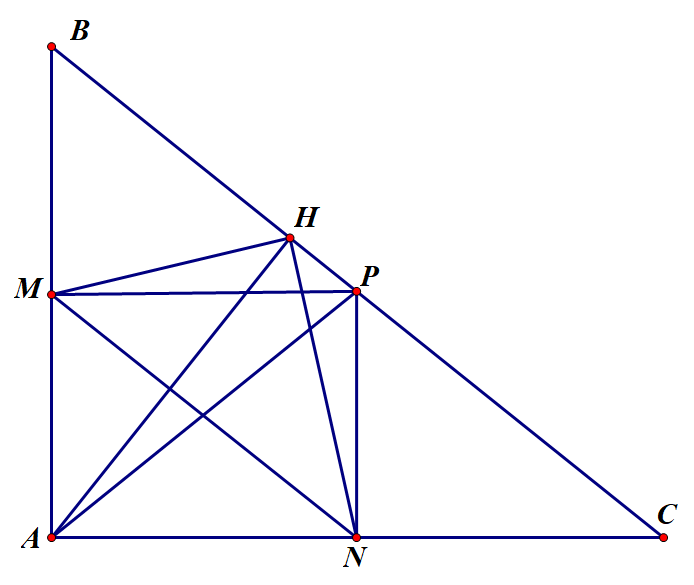
Xét tam giác vuông AHC vuông tại H có HN là đường trung tuyến $\Rightarrow N H = N C = N A$ .

Lại có $N A = M P \Rightarrow N H = M P$ .

Tứ giác MNPH có $M N // H P$ (MN là đường trung bình tam giác ABC) và $N H = M P \Rightarrow M N P H$ là hình thang cân.

Câu 11:

Cho tam giác ABC vuông tại $(A B < A C)$ , đường cao AH. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC.

Cho biết $B C = 10 c m$ và diện tích tam giác ABC bằng $20 c m^{2}$ . Tính diện tích tam giác AHP.

Xem đáp án

Phương pháp:

Sử dụng dấu hiệu nhận biết và tính chất của hình bình hành, hình chữ nhật, hình thang cân và công thức tính diện tích tam giác.

Cách giải:

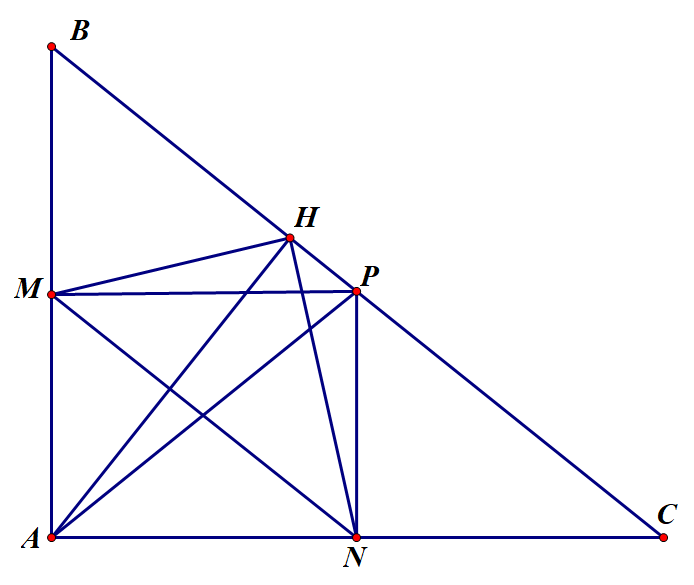
Media VietJack

$S_{A B C} = 20 \Rightarrow \frac{1}{2} A H . B C = 20 \Rightarrow \frac{1}{2} A H .10 = 20$

$\Rightarrow A H = 4 (c m)$

Lại có $A P = \frac{1}{2} B C = 10 (c m)$ .

Áp dụng định lý Pitago ta có:

$A H^{2} + H P^{2} = A P^{2}$

$\Rightarrow H P^{2} = A P^{2} - A H^{2}$

$\Rightarrow H P^{2} = 10^{2} - 4^{2}$

$\Rightarrow H P^{2} = 84 \Rightarrow H P = \sqrt{84} = 2 \sqrt{21} (c m)$

Diện tích tam giác AHP là: $\frac{1}{2} A H . H P = \frac{1}{2} .4.2 \sqrt{21} = 4 \sqrt{21} (c m^{2})$ .

Câu 12:

Cho $x^{2} + 2 x - 2 = 0$ . Tính giá trị biểu thức $M = x^{4} + 16 x + 2007$ .

Xem đáp án

Phương pháp:

Sử dụng điều kiện để biểu diễn biểu thức đã cho theo điều kiện.

Có thể phân tích biểu thức hoặc sử dụng hệ quả của phép chia đa thức.

Cách giải:

Theo giả thiết: $x^{2} + 2 x - 2 = 0$ .

$M = x^{4} + 16 x + 2007$

$= x^{4} + 2 x^{3} - 2 x^{2} - 2 x^{3} - 4 x^{2} + 4 x + 6 x^{2} + 12 x - 12 + 2019$

$= (x^{4} + 2 x^{3} - 2 x^{2}) - (2 x^{3} + 4 x^{2} - 4 x) + (6 x^{2} + 12 x - 12) + 2019$

$= x^{2} (x^{2} + 2 x - 2) - 2 x (x^{2} + 2 x - 2) + 6 (x^{2} + 2 x - 2) + 2019$ $= 0 + 0 + 0 + 2019$ $= 2019$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bộ 14 đề thi Học kì 1 Toán 8 có đáp án

Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 9

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương