20 câu hỏi trắc nghiệm thuộc Dạng 3: Trắc nghiệm Hàm số có đáp án

Câu 1:

Tìm m để đường thẳng (d): $y = (m - 1) x + \frac{1}{2} m^{2} + m$ đi qua điểm

Chứng minh rằng parabol (P) luôn cắt đường thẳng d tịa hai điểm phân biệt A và B. Gọi

x_{1}; x_{2}

là hoàng độ hai điểm A, B. Tìm m sao cho

x_{1}^{2} + x_{2}^{2} + 6 x_{1} x_{2} > 2019

Xem đáp án

Phương trình hoành độ giao điểm của P và d là:

$\frac{1}{2} x^{2} = (m - 1) x + \frac{1}{2} m^{2} + m$ $\Leftrightarrow \frac{1}{2} x^{2} - (m - 1) x - \frac{1}{2} m^{2} - m = 0 (1)$

Ta có

Δ = {[- (m - 1)]}^{2} - 4. \frac{1}{2} . (- \frac{1}{2} m^{2} - m)

Δ = m^{2} - 2 m + 1 + m^{2} + 2 m

Δ = 2 m^{2} + 1 > 0

với mọi m

Suy ra phương trình 1 luôn có hai nghiệm phân biết với mọi m

Nên P luôn cắt d tại hai điểm phân biệt A và B

Theo vi-ét ta có:

\{\begin{matrix} x_{1} + x_{2} = 2 (m - 1) \\ x_{1} . x_{2} = - m^{2} - 2 m \end{matrix}

Theo đề ta có: $x_{1}^{2} + x_{2}^{2} + 6 x_{1} x_{2} > 2019$ $\Leftrightarrow {[2 (m - 1)]}^{2} + 4 (- m^{2} - 2 m) - 2019 > 0$ $\Leftrightarrow 4 m^{2} - 8 m + 4 - 4 m^{2} - 8 m - 2019 > 0$ $\Leftrightarrow - 16 m - 2015 > 0$ $\Leftrightarrow m < \frac{2015}{16}$

Câu 2:

Tìm tham số m để đường thẳng $y = (m - 1) x + 2018$ có hệ số góc bằng .3

Xem đáp án

+ Đường thẳng $y = (m - 1) x + 2018$ có hệ số góc bằng $\Leftrightarrow m - 1 = 3$

$\Leftrightarrow m = 4$

Vậy $m = 4$ .

Câu 3:

Cho hàm số $y = \frac{1}{2} x^{2}$ có dồ thị $(P) : y = x - 2 m .$ Vẽ đồ thị (P) tìm tất cả các giá trị của m sao cho (d) cắt (P) tại điểm có hoành độ bằng – 1

Xem đáp án

Vì (d) cắt (P) tại điểm có hoành độ là -1 $\Rightarrow x = - 1; y = \frac{1}{2} . {(- 1)}^{2} = \frac{1}{2}$

$t h a y x = - 1; y = \frac{1}{2} t a c ó : \frac{1}{2} = - 1 - 2 m \Leftrightarrow m = \frac{- 3}{4}$

Vậy $m = \frac{- 3}{4}$ là giá trị cần tìm.

Câu 4:

Cho parabol (P): $y = 2 x^{2}$ và đường thằng (d): $y = 2 x + m$ (m là tham số)

a) Vẽ parabol (P).

b) Với những giá trị nào của m thì (P) và (d) chỉ có một điểm chung. Tìm tọa độ điểm chung đó.

Xem đáp án

Bảng giá trị của (P)

	– 2	– 1	0	1	2
	8	2	0	2	8

Phương trình hoành độ giao điểm của (P) và (d) là:

$2 x^{2} = 2 x + m \Leftrightarrow 2 x^{2} - 2 x - m = 0 (1)$

.(P) và (d) chỉ có một điểm chung khi phương trình (1) có nghiệm kép

=> $Δ' = 0$ hay $2 m + 1 = 0 \Leftrightarrow m = - \frac{1}{2}$ .

Khi $m = - \frac{1}{2}$ phương trình (1) có nghiệm kép $x_{1} = x_{2} = \frac{1}{2} \Rightarrow y_{1} = y_{2} = \frac{1}{2}$ .

Vậy tọa độ điểm chung khi đó là $(\frac{1}{2}; \frac{1}{2})$ .

Câu 5:

Tìm tọa độ giao điểm A , B của đồ thị hai hàm số

y = x^{2}

và y=x+2 . Gọi D , C lần lượt là hình chiếu vuông góc của A , B lên trục hoành. Tính diện tích tứ giác ABCD .

Xem đáp án

Phương trình hoành độ giao điểm $x^{2} - x - 2 = 0$ .

Giải phương trình tìm được $x_{1} = - 1$ ; $x_{2} = 2$ . Ta xác định được điểm $A (- 1; 1)$ , $B (2; 4)$ .

Do đó, hình chiếu của A , Btrên trục hoành lần lượt là D(-1;0), C(2;0).

Khi đó , $A B C D$ là hình thang vuông tại C, D có các đáy là $A D = 1$ , $B C = 4$ , đường cao $C D = 3$ .

Diện tích cần tìm là $S_{A B C D} = \frac{1}{2} (A D + B C) C D = \frac{1}{2} .5.3 = \frac{15}{2}$ (đơn vị diện tích).

Câu 6:

Trong mặt phẳng tọa độ $(O x y)$ , cho parabol (P): $y = \frac{1}{2} x^{2}$ và đường thẳng (d): $y = (2 m - 1) x + 5$ .

a) Vẽ đồ thị của (P).

b) Tìm m để đường thẳng (d) đi qua điểm $E (7; 12)$ .

c) Đường thẳng cắt parabol (P) tại hai điểm A, B. Tìm tọa độ của A, B và tính diện tích tam giác OAB.

Xem đáp án

Bảng giá trị :

x	-2	-1	0	1	2
x²	2	1/2	0	1/2	2

Đồ thị

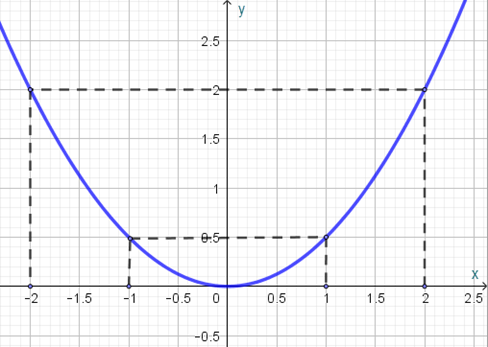
b) Đường thẳng (d): $y = (2 m - 1) x + 5$ đi qua điểm $E (7; 12)$ , ta có $12 = (2 m - 1) .7 + 5$

$\Leftrightarrow 2 m - 1 = 1 \Leftrightarrow m = 1$

c) Phương trình hoành độ giao điểm của (P) và đường thẳng y = 2 là :

$\frac{1}{2} x^{2} = 2 \Leftrightarrow x^{2} = 4 \Leftrightarrow [\begin{matrix} x = 2 \\ x = - 2 \end{matrix}$

AB = 4, H(0 ;2) là giao điểm của đường thẳng y = 2 và trục tung

Diện tích tam giác OAB : $S_{Δ O A B} = \frac{1}{2} A B . O H = 4$ (đvdt)

Câu 7:

Trong mặt phẳng tọa độ Oxy cho các đường thẳng có phương trình

(d_{1}) : y = x + 2

,

(d_{2}) : y = - 2

,

(d_{3}) : y = (k + 1) x + k

. Tìm để các đường thẳng trên đồng quy.

Xem đáp án

Tọa độ giao điểm của (d₁ ) và (d₂ )là nghiệm của hệ $\{\begin{cases} y = x + 2 \\ y = - 2 \end{cases} \Leftrightarrow \{\begin{cases} x = - 4 \\ y = - 2. \end{cases}$

Do đó ba đường thẳng trên đồng quy khi đi qua điểm $(- 4; - 2)$ .

Suy ra $- 2 = - 4 (k + 1) + k \Leftrightarrow 3 k = - 2 \Leftrightarrow k = - \frac{2}{3}$ .

Câu 8:

Vẽ đồ thị của các hàm số $y = - \frac{1}{2} x^{2}$ và $y = x - 4$ trên cùng một mặt phẳng tọa độ. Gọi A và B là các giao điểm của đồ thị hai hàm số trên. Tính bán kính của đường tròn ngoại tiếp tam giác OAB, với O là gốc tọa độ ( đơn vị đo trên các trục tọa độ là centimét).

Xem đáp án

Vẽ đồ thị hàm số: .

x	-4	-2		0	2	4
y	-8	-2		0	-2	-8

Khi đó đồ thị hàm số có hình dạng là 1 Parabol và đi qua các điểm (-4;-8); (-2;-2) ; (0;0) ; (2;-2); 4;-8).

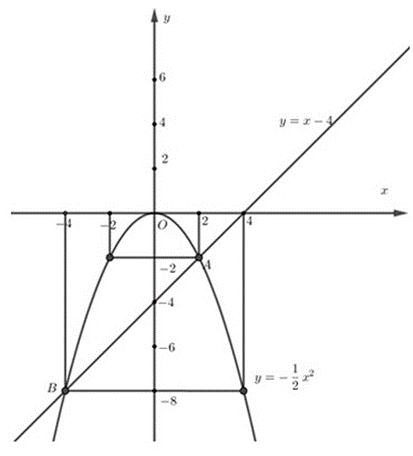
Vẽ đồ thị của các hàm số y=1/2x^2 và y=x-4 trên cùng một mặt phẳng tọa độ. Gọi A và B là các giao điểm của đồ thị hai hàm số trên. Tính bán kính của đường tròn ngoại tiếp tam giác OAB, với O là gốc tọa độ ( đơn vị đo trên các trục tọa độ là centimét). (ảnh 3)

+) Phương trình hoành độ giao điểm của hàm số và là:

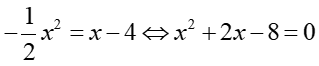
Câu 9:

Cho Parabol (P):

y = 2 x^{2}

và đường thẳng (d) có phương trình y=3x+m-1. Tìm tất cả các giá trị tham số m để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt

Xem đáp án

Ta có phương trình hoành độ giao điểm của (P) và (d) là : $2 x^{2} = 3 x + m - 1 \Leftrightarrow 2 x^{2} - 3 x + 1 - m = 0$ (1)

$Δ = {(- 3)}^{2} - 4.2. (1 - m) = 9 - 8 + 8 m = 8 m + 1$

Để (d) cắt (P) tại hai điểm phân biệt thì phương trình (1) có hai nghiệm phân biệt $\Rightarrow Δ > 0 \Leftrightarrow 8 m + 1 > 0 \Leftrightarrow m > - \frac{1}{8}$

Câu 10:

Trong hệ tọa độ cho Parabol $y = x^{2} (P)$ và đường thẳng (d) có phương trình: $y = (m - 1) x + m^{2} - 2 m + 3 (d)$ .

Chứng minh với mọi giá trị của m thì (d) luôn cắt (P) tại hai điểm phân biệt.

Giả sử cắt (P) tại hai điểm phân biệt A,B . Tìm m để tam giác OAB cân tại O. Khi đó tính diện tích tam giác OAB.

Xem đáp án

Xét PT hoành độ giao điểm: $x^{2} = (m - 1) x + m^{2} - 2 m + 3 \Leftrightarrow x^{2} - (m - 1) x - (m^{2} - 2 m + 3) = 0 (*)$

Ta có $m^{2} - 2 m + 3 = {(m - 1)}^{2} + 2 > 0 (\forall m) \Rightarrow$ Phương trình (*) luôn có 2 nghiệm trái dấu

thì luôn cắt (P) tại hai điểm phân biệt.

Để tam giác AOB cân tại O thì Oy là đường trung trực của đoạn thẳng AB hay đường thẳng d song song Ox khi đó: $m - 1 = 0 \Leftrightarrow m = 1$

Với đường thẳng d có phương trình: , tọa độ 2 giao điểm A, B là $(\pm \sqrt{2}; 2)$ . Khi đó khoảng cách từ O đến AB là . Độ dài đoạn thẳng $A B = 2 |x_{1}| = 2 \sqrt{2}$

Diện tích tam giác AOB là: $S_{Δ A O B} = \frac{1}{2} A B . h = \frac{1}{2} .2 \sqrt{2} .2 = 2 \sqrt{2}$

Vậy để tam giác AOB cân tại O thì m=1. Khi đó $S_{Δ A O B} = 2 \sqrt{2}$ (đvdt)

Câu 11:

Cho hàm số: $y = f (x)$ với $f (x)$ là một biểu thức đại số xác định với $\forall x \in ℝ^{*}$ .

Biết rằng: $f (x) + 3 f (\frac{1}{x}) = x^{2} (\forall x \neq 0)$ . Tính $f (2)$ .

Xem đáp án

Vì $f (x) + 3 f (\frac{1}{x}) = x^{2} (\forall x \neq 0)$

Nên ta có:

\{\begin{matrix} f (2) + 3 f (\frac{1}{2}) = 4 \\ f (\frac{1}{2}) + 3 f (2) = \frac{1}{4} \end{matrix} \Leftrightarrow \{\begin{matrix} f (2) + 3 f (\frac{1}{2}) = 4 \\ 3 f (\frac{1}{2}) + 9 f (2) = \frac{3}{4} \end{matrix}

\Rightarrow 8 f (2) = - \frac{13}{4} \Rightarrow f (2) = - \frac{13}{32}

Câu 12:

a)

Cho hai hàm số $y = \frac{1}{4} x^{2}$ và $y = x - 1$ có đồ thị lần lượt là (P) và (d)

a) Vẽ hai đồ thị (P) và (d) trên cùng mặt phẳng tọa độ.

a) Tìm tọa độ giao điểm của hai đồ thị (P) và (d).

Xem đáp án

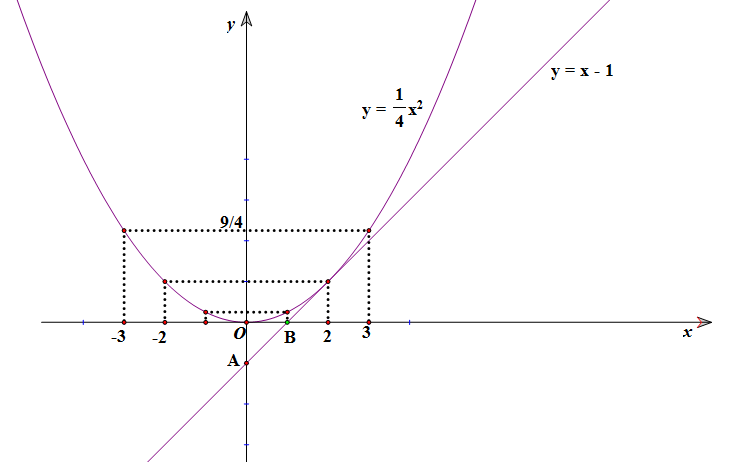
Cho hai hàm số y=1/4x^2 và y=x+1 có đồ thị lần lượt là (P) và (d). a) Vẽ hai đồ thị (P) và (d) trên cùng mặt phẳng tọa độ. (ảnh 1)

a) Tìm tọa độ giao điểm của hai đồ thị (P) và (d).

Phương trình hoành độ giao điểm của (P) và (d) là: $\frac{1}{4} x^{2} = x - 1 \Leftrightarrow x^{2} = 4 x - 4 \Leftrightarrow x^{2} - 4 x + 4 = 0 \Leftrightarrow {(x - 2)}^{2} = 0 \Leftrightarrow x = 2$

Thay x=2 vào $y = \frac{1}{4} x^{2}$ ta được $y = \frac{1}{4} {.2}^{2} = 1$

Vậy tọa độ giao điểm của hai đồ thị (P) và (d) là (2;1)

Câu 13:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng $(d) : y = - 3 x + b$ và parabol $(P) : y = 2 x^{2}$

a) Xác định hệ số b để (d) đi qua điểm $A (0; - 1)$

b) Với b=-1 , tìm tọa độ giao điểm của (d) và (P) bằng phương pháp đại số

Xem đáp án

a) Vì $(d) : y = - 3 x + b$ đi qua $A (0; - 1)$ $\Rightarrow 1 = - 3.0 + b \Leftrightarrow b = 1$

a) Với $b = - 1$ ta có $(d) : y = - 3 x - 1$

Phương trình hoành độ giao điểm của (d) và (P) là $2 x^{2} = - 3 x - 1 \Leftrightarrow 2 x^{2} + 3 x + 1 = 0$

Phương trình có dạng $a - b + c = 0 \Rightarrow [\begin{array}{l} x = - 1 \Rightarrow y = 2 \\ x = \frac{- 1}{2} \Rightarrow y = \frac{1}{2} \end{array}$

Vậy tọa độ giao điểm của (d) và (P) là $(- 1; 2) (- \frac{1}{2}; \frac{1}{2})$

Câu 14:

Cho hai đường thẳng $(d_{1}) : y = x + 1$ và $(d_{2}) : y = m x + 2 - m$ (với m là tham số, ).

Gọi $A (x_{0}; y_{0})$ là giao điểm của $(d_{1})$ với $(d_{2})$ . Tính giá trị của biểu thức $T = x_{0}^{2} + y_{0}^{2}$

Xem đáp án

Ta có phương trình hoành độ giao điểm là $x + 1 = m x + 2 - m$

$\Leftrightarrow x - m x = 1 - m$ $\Leftrightarrow x (1 - m) = 1 - m$

$\Leftrightarrow x = 1 \Rightarrow y = 1 + 1 = 2$

Nên $T = x_{0}^{2} + y_{0}^{2} = 1^{2} + 1^{2} = 2$

Câu 15:

Tìm giá trị của m để đồ thị hàm số y = mx² đi qua điểm A(2;4).

Xem đáp án

Vì hàm số ${y=mx}^{2}$ đi qua điểm $A (2; 4) \Rightarrow \{\begin{cases} x = 2 \\ y = 4 \end{cases} .$

Thay vào hàm số ta có $4 = m {.2}^{2} \Rightarrow m = 1$

Vậy $m = 1$

Câu 16:

Trong mặt phẳng tọa độ Oxy , cho parabol (P) có phương trình $y = x^{2}$ và đường thẳng (d) có phương trình $y = 2 (m - 1) x + m + 1$ (với là tham số).

Chứng minh rằng (d) luôn cắt (P) tại hai điểm phân biệt với mọi giá trị của .

Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ $x_{1}, x_{2}$ thỏa mãn $x_{1} + 3 x_{2} - 8 = 0$ .

Xem đáp án

Phương trình hoành độ giao điểm của và :

$x^{2} = 2 (m - 1) x + m + 1 \Leftrightarrow x^{2} - 2 (m - 1) x - m - 1 = 0$ (1)

Số nghiệm phương trình (1) là số giao điểm của và .

Ta có $Δ' = {(m - 1)}^{2} - (- m - 1) = m^{2} - m + 2$ .

Ta có $m^{2} - m + 2 = {(m - \frac{1}{2})}^{2} + \frac{7}{4} > 0$ với mọi giá trị của .

Suy ra $Δ' > 0$ với mọi giá trị của .

phương trình (1) luôn có hai nghiệm phân biệt với mọi hay luôn cắt tại hai điểm phân biệt.

b) Tìm các giá trị của để cắt tại hai điểm phân biệt có hoành độ $x_{1}, x_{2}$ thỏa mãn $x_{1} + 3 x_{2} - 8 = 0$ .

Theo câu a), ta có là hai nghiệm phương trình (1) nên theo Viet: $\{\begin{cases} x_{1} + x_{2} = 2 (m - 1) = 2 m - 2 \\ x_{1} x_{2} = - m - 1 \end{cases}$

Kết hợp giả thiết ta có $\{\begin{cases} x_{1} + x_{2} = 2 m - 2 (2) \\ x_{1} x_{2} = - m - 1 (3) \\ x_{1} + 3 x_{2} - 8 = 0 (4) \end{cases}$

Từ (2) và (4), tính được $x_{1} = 3 m - 7; x_{2} = - m + 5$

Thay vào (3), tính được $(5 - m) (3 m - 7) = - m - 1 \Leftrightarrow 3 m^{2} - 23 m + 34 = 0 \Leftrightarrow [\begin{array}{l} m = 2 \\ m = \frac{17}{3} \end{array}$ .

Vậy $m = 2; m = \frac{17}{3}$ thỏa mãn đề bài.

Câu 17:

Tìm các giá trị của tham số m để đường thẳng (dm):

(d_{m}) : y = (m^{2} + m - 4) x + m - 7

song song với đường thẳng (d): y=2x-5

Xem đáp án

$\begin{array}{l} (d_{m}) / / d \{\begin{cases} m^{2} + m - 4 = 2 \\ m - 7 \neq - 5 \end{cases} \Leftrightarrow \{\begin{cases} m^{2} + m - 6 = 0 \\ m \neq 2 \end{cases} \\ \Leftrightarrow \{\begin{cases} [\begin{array}{l} m = 2 \\ m = - 3 \end{array} \\ m \neq 2 \end{cases} \Leftrightarrow m = - 3 \\ m = - 3 \end{array}$

Câu 18:

Cho hàm số $y = - \frac{1}{2} x^{2}$ có đồ thị (P) và đường thẳng $(d) : y = 3 - 4 x$ . Lập phương trình đường thẳng $(Δ)$ song song với (d) và cắt (P) tại điểm M có hoành độ bằng 2

Xem đáp án

Gọi $(Δ)$ có phương trình $y = a x + b (a \neq 0)$

$\begin{array}{l} Vì (Δ) / / (d) \Rightarrow a = - 4; b \neq 3 \end{array}$

Vì (d) căt (P) tại điểm có hoành độ là 2 $\Rightarrow \{\begin{cases} y = - \frac{1}{2} {.2}^{2} = - 2 \\ x = 2 \end{cases}$

\begin{array}{l} t h a y v à o (Δ) \Rightarrow - 2 = - 4.2 + b \Leftrightarrow b = 6 (t m) \\ Vậy (Δ) c ầ n l ậ p : y = - 4 x + 6 \end{array}

Câu 19:

Cho đường thẳng

d : y = (m - 1) x + n .

Tìm các giá trị của để đường thẳng d đi qua điểm

A (1, - 1)

và có hệ số góc bằng -3

Xem đáp án

Đường thẳng đi qua điểm $A (1, - 1)$ nên $- 1 = m - 1 + n \Leftrightarrow m + n = 0 (1)$

Đường thẳng d có hệ số góc bằng -3 nên $m - 1 = - 3 \Leftrightarrow m = - 2 (2)$

Từ (1) và (2) ta được $m = - 2, n = 2.$

Câu 20:

Cho hai hàm số y = - x +2 và $y = x^{2}$ có đồ thị lần lượt là (d) và (P)

1) Vẽ (d) và (P) trên cùng một hệ trục tọa độ

2) Bằng phép toán tìm tọa độ giao điểm của (d) và (P)

Xem đáp án

Vẽ (P) và (d) trên cùng trục tọa độ

+)Vẽ đồ thị hàm số (d): y = - x +2

x	0	2
y= - x + 2	2	0

+) Vẽ đồ thị hàm số (P): $y = x^{2}$

x	- 2	- 1	0	1	2
y=	4	1	0	1	4

1.) Bằng phép toán tìm tọa độ giao điểm (d) và (P)

Ta có phương trình hoành độ giao điểm của hai đồ thị

$\begin{array}{l} - x + 2 = x^{2} \Leftrightarrow x^{2} + x - 2 = 0 \\ Δ = 1^{2} - 4.1. (- 2) = 9 > 0 \\ \Rightarrow [\begin{array}{l} x_{1} = \frac{- 1 - \sqrt{9}}{2} = - 2 \Rightarrow y = 4 \\ x_{2} = \frac{- 1 + \sqrt{9}}{2} = 1 \Rightarrow y = 1 \end{array} \end{array}$

Vậy hai đồ thị cắt nhau tại 2 điểm phân biệt $A (- 2; 4)$ và B(1;1)

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bộ đề Ôn tập Toán 9 thi vào 10 năm 2019 có đáp án

Dạng 3: Trắc nghiệm Hàm số có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm