Bài 10: Số nguyên tố. Hợp số - SBT Toán 6 Bộ Cánh diều
-
7284 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho các số 3; 13; 17; 18; 25; 39; 41. Trong các số đó:
a) Số nào là số nguyên tố? Vì sao?
b) Số nào là hợp số? Vì sao?
Xem đáp án
a) Trong các số đã cho các số là số nguyên tố là: 3; 13; 17; 41 vì:
+) 3 chỉ có hai ước là 1 và 3 nên 3 là số nguyên tố.
+) 13 chỉ có hai ước là 1 và 13 nên 13 là số nguyên tố.
+) 17 chỉ có hai ước là 1 và 17 nên 17 là số nguyên tố.
+) 41 chỉ có hai ước là 1 và 41 nên 41 là số nguyên tố.
b) Trong các số đã cho các số là hợp số là: 18; 25; 39 vì:
+) 18 có các ước là 1; 2; 3; 6; 9 và 18 nhiều hơn hai ước nên 18 là hợp số.
+) 25 có các ước là: 1; 5; 25 nhiều hơn hai ước nên 25 là hợp số.
+) 39 có các ước là 1; 3; 13; 39 nhiều hơn hai ước nên 39 là hợp số.
Câu 2:
a) Tìm các ước nguyên tố của các số sau: 12; 36; 43.
b) Tìm các ước không phải là số nguyên tố của các số sau: 21; 35; 47.
Xem đáp án
a) +) Lần lượt lấy 12 chia cho các số từ 1 đến 12, ta được: Ư(12) = {1; 2; 3; 4; 6; 12}.
Trong các ước của 12, ước nguyên tố là: 2; 3.
+) Lần lượt lấy 36 chia cho các số từ 1 đến 36, ta được Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}.
Trong các ước trên, ước nguyên tố là: 2; 3.
+) Lần lượt lấy 43 chia cho các số từ 1 đến 43, ta được Ư(43) = {1; 43}.
Trong các ước của 43, ước nguyên tố là 43.
b) +) Lần lượt lấy 21 chia cho các số từ 1 đến 21 ta được Ư(21) = {1; 3; 7; 21}.
Trong các ước trên, các ước không phải ước nguyên tố là: 1; 21.
+) Lần lượt lấy 35 chia cho các số từ 1 đến 35 ta được Ư(35) = {1; 5; 7; 35}.
Trong các ước trên, các ước không phải ước nguyên tố là: 1; 35.
+) Lần lượt lấy 47 chia cho các số từ 1 đến 47 ta được Ư(47) = {1; 47}.
Trong các ước trên, các ước không phải ước nguyên tố là: 1.
Câu 3:
Hai bạn Ân và Huệ tranh luận tính đúng, sai của các phát biểu sau:
a) Có ba số lẻ liên tiếp đều là số nguyên tố;
b) Có hai số nguyên tố mà tổng của chúng là một số lẻ;
c) Mọi số nguyên tố đều là số lẻ.
d) Tổng của hai số nguyên tố bất kì là một số chẵn.
Hãy giúp các bạn tìm ra phát biểu đúng và phát biểu sai. Cho ví dụ cụ thể.
Xem đáp án
+) Ta có ba số lẻ liên tiếp là: 3; 5; 7 và chúng đều là số nguyên tố. Do đó a) đúng.
+) Ta có 2 và 3 là hai số nguyên tố và tổng của chúng là 2 + 3 = 5 cũng là một số lẻ. Do đó b) đúng.
+) 2 là một số nguyên tố, nhưng 2 không là số lẻ. Do đó c) sai.
+) Ta có 2 và 3 là hai số nguyên tố và tổng của chúng là 2 + 3 = 5 cũng là một số lẻ. Do đó d) sai.
Câu 4:
Ba số nguyên tố phân biệt có tổng là 106. Số lớn nhất trong ba số nguyên tố đó có thể lớn nhất bằng bao nhiêu?
Xem đáp án
Tổng ba số nguyên tố này là 106 là một số chẵn nên trong ba số nguyên tố cần tìm phải có một số nguyên tố chẵn là 2.
Suy ra tổng hai số còn lại là: 106 – 2 = 104 và hai số này phải lớn hơn 2 và nhỏ hơn 102.
Ta thấy 101 là số nguyên tố lớn nhất nhỏ hơn 102 và 104 – 101 = 3 cũng là một số nguyên tố.
Vậy số cần tìm là: 101.
Câu 5:
Tìm số nguyên tố p thỏa mãn mỗi điều kiện sau:
a) p + 1 cũng là số nguyên tố;
b) p + 2 và p + 4 đều là số nguyên tố;
c) p + 2; p + 6; p + 14; p + 16 đều là số nguyên tố.
Xem đáp án
a) p nguyên tố, p + 1 cũng là số nguyên tố
Nếu p = 2 thì p + 1 = 3 là số nguyên tố.
Nếu p > 2 thì p là số lẻ lớn hơn 2 suy ra p + 1 là số chẵn lớn hơn 2. Do đó p + 1 không là số nguyên tố (không thỏa mãn).
Vậy p = 2.
b) p nguyên tố, p + 2 và p + 4 đều là số nguyên tố.
Nếu p = 2 thì p + 2 = 4, p + 4 = 6 đều là hợp số (không thỏa mãn).
Nếu p = 3 thì p + 2 = 5, p + 4 = 7 đều là các số nguyên tố (thỏa mãn).
Nếu p > 3:
+) p chia cho 3 dư 1 thì p + 2 chia hết cho 3 và p + 2 > 3 nên p + 2 là hợp số (không thỏa mãn).
+) p chia cho 3 dư 2 thì p + 4 chia hết cho 3 và p + 4 > 3 nên p + 4 là hợp số (không thỏa mãn).
Vậy p = 3.
c) p + 2; p + 6; p + 14; p + 18 đều là số nguyên tố
Nếu p = 2 thì p + 2 = 4; p + 6 = 8; p + 14 = 16; p + 18 = 20 đều là hợp số (không thỏa mãn).
Nếu p = 3 thì p + 2 = 5; p + 14 = 17; là số nguyên tố và p + 6 = 9; p + 18 = 21 là hợp số (không thỏa mãn).
Nếu p = 5 thì p + 2 = 7; p + 6 = 11; p + 14 = 19; p + 18 = 23 là các số nguyên tố (thỏa mãn).
Nếu p > 5:
+) p chia 5 dư 1 thì p + 14 chia hết cho 5 và p + 14 > 5 nên p + 14 là hợp số (không thỏa mãn).
+) p chia 5 dư 2 thì p + 18 chia hết cho 5 và p + 18 > 5 nên p + 18 là hợp số (không thỏa mãn).
+) p chia 5 dư 3 thì p + 2 chia hết cho 5 và p + 2 > 5 nên p + 2 là hợp số (không thỏa mãn).
+) p chia 5 dư 4 thì p + 6 chia hết cho 5 và p + 6 > 5 nên p + 6 là hợp số (không thỏa mãn).
Vậy p = 5.
Câu 6:
Tìm số tự nhiên n sao cho:
a) 7n là số nguyên tố;
b) 3n + 18 là số nguyên tố.
Xem đáp án
a) 7n là số nguyên tố
+) n = 0 thì 7n = 0 không là số nguyên tố (không thỏa mãn).
+) n = 1 thì 7n = 7 là số nguyên tố (thỏa mãn).
+) n > 1 thì 7n > 7 mà 7n chia hết cho 7 nên 7n có nhiều hơn hai ước. Do đó 7n không là số nguyên tố (không thỏa mãn).
Vậy n = 1.
b) 3n + 18 là số nguyên tố
+) n = 0 thì 3n + 18 = 19 là số nguyên tố (thỏa mãn).
+) n > 1 thì 3n + 18 chia hết cho 3 và 3n + 18 > 3 nên 3n + 18 là hợp số (không thỏa mãn).
Vậy n = 0.
Câu 7:
Chứng tỏ rằng các tổng sau đây là hợp số:
a) ;
b) .
Xem đáp án
a) 
Vì 1 001 = 11.91 nên 1001 chia hết cho 11; 22 = 2.11 chia hết cho 11 nên 
chia hết cho 11.
Mà 
Do đó 
Vậy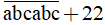 
là hợp số.
b) 
Vì 1001 = 13.77 nên 1 001 chia hết cho 13 và 39 = 3.13 chia hết cho 13 nên 
chia hết cho 13.
Mà 
Do đó 
Vậy 
là hợp số.
Câu 8:
Chứng tỏ rằng mọi ước nguyên tố của 2.3.4…2 020. 2 021 – 1 đều lớn hơn 2 021.
Xem đáp án
Đặt A = 2.3.4…2 020. 2 021 – 1
Gọi k là ước nguyên tố của A = 2.3.4…2 020. 2 021 – 1 (k >1).
Do đó A chia hết cho k.
Giả sử k ≤ 2021, khi đó 2.3.4…2 020. 2 021 chia hết cho k mà A cũng chia hết cho k nên 1 phải chia hết cho k hay k = 1 (vô lý).
Suy ra giả sử sai.
Vậy k > 2021.
Câu 9:
Tìm chữ số x để mỗi số sau là hợp số
a) ;
b) .
Xem đáp án
Vì x là chữ số nên x ∈ .
a) Nếu x ∈ {0; 2; 4; 6; 8} thì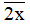 
chia hết cho 2 nên 
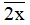là hợp số (thỏa mãn).
Nếu x = 5 thì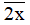 
chia hết cho 5 nên 
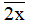là hợp số (thỏa mãn).
Nếu x ∈ {1; 7} thì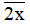 
chia hết cho 3 nên 
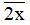là hợp số (thỏa mãn).
Nếu x ∈ {3; 9} thì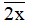 
= 23 và 
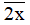= 29 là các số nguyên tố (không thỏa mãn).
Vậy x ∈ {0; 1; 2; 4; 5; 6; 7; 8}.
b) Nếu x ∈ {0; 2; 4; 6; 8} thì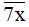 
chia hết cho 2 nên 
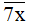là hợp số (thỏa mãn).
Nếu x = 5 thì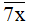 
chia hết cho 5 nên 
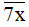là hợp số (thỏa mãn).
Nếu x = 7 thì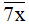 
chia hết cho 11 nên 
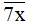là hợp số (thỏa mãn).
Nếu x ∈ {1; 3; 9} thì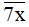 
= 71, 
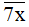= 73;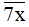 
= 79 là các số nguyên tố (không thỏa mãn).
Vậy x ∈ {0; 2; 4; 5; 6; 7; 8}.
Câu 10:
Tìm số tự nhiên a để trong 10 số tự nhiên sau: a + 1; a + 2; a + 3; …; a + 9; a + 10 có nhiều số nguyên tố nhất.
Xem đáp án
+) a = 0
10 số tự nhiên đó lần lượt là: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10.
Trong đó có 4 số nguyên tố: 2; 3; 5; 7.
+) a = 1
10 số tự nhiên đó lần lượt là: 2; 3; 4; 5; 6; 7; 8; 9; 10; 11.
Trong đó có 5 số nguyên tố là: 2; 3; 5; 7; 11.
+) a > 1
- a chẵn thì a + 2; a + 4; a + 6; a + 8; a + 10 là các số chẵn nên chúng là hợp số.
Còn các số a + 1; a + 3; a + 5; a + 7; a + 9 là các số lẻ mà trong 3 số lẻ liên tiếp luôn tồn tại một số chia hết cho 3. Do đó có ít nhất một số là hợp số trong 5 số này.
Suy ra có ít nhất 5 số là hợp số trong dãy các số trên nghĩa là số số nguyên tố < 5 số.
- a chẵn thì a + 1; a + 3; a + 5; a + 7; a + 9 là các số chẵn nên chúng là hợp số.
Còn các số a + 2; a + 4; a + 6; a + 8; a + 10 là các số lẻ mà trong 3 số lẻ liên tiếp luôn tồn tại một số chia hết cho 3. Do đó có ít nhất một số là hợp số trong 5 số này.
Suy ra có ít nhất 5 số là hợp số trong dãy các số trên nghĩa là số số nguyên tố < 5 số.
Vậy a = 1 để 10 số tự nhiên có nhiều số nguyên tố nhất.