Bài 7: Quan hệ chia hết Tính chất chia hết - Bộ Cánh diều
-
6577 lượt thi
-
22 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Lớp 6A có 6 tổ học sinh. Để tổ chức liên hoan cho lớp, cô Ngân đã mua 42 chiếc bánh ngọt và 45 quả quýt.
Cô Ngân có thể chia đều số bánh ngọt cho 6 tổ được không?
Cô Ngân có thể chia đều số quả quýt cho 6 tổ được không?
 Xem đáp án
Xem đáp án
Để biết cô Ngân có chia đều số bánh ngọt và số quả quýt cho 6 tổ hay không thì ta thực hiện phép chia.
Ta có: 42 : 6 = 7 ; 45 : 6 = 7 (dư 3).
Khi đó ta nói 42 chia hết cho 6 và 45 không chia hết cho 6 (qua bài học dưới này ta sẽ tìm hiểu kĩ hơn)
Vậy cô Ngân có thể chia đều số bánh ngọt cho 6 tổ và không thể chia đều số quả quýt cho 6 tổ.
Câu 2:
a) Thực hiện các phép tính 42 : 6 và 45 : 6
b) Trong hai phép chia trên, phép chia nào là phép chia hết, phép chia nào là phép chia có dư?
 Xem đáp án
Xem đáp án
a) 42 : 6 = 7 ; 45 : 6 = 7 (dư 3).
b) Khi đó ta có:
* 42 = 6 . 7 nên 42 chia hết cho 6
* Do 45 chia cho 6 dư 3 nên 45 không chia hết cho 6.
Câu 3:
Viết ngày và tháng sinh của em dưới dạng ngày a tháng b. Chỉ ra một ước của a và hai bội của b.
 Xem đáp án
Xem đáp án
Giả sử em sinh ngày 14 tháng 6 năm 2010. Khi đó a = 14 và b = 6.
Ta có: 14 = 2 . 7 nên 14 chia hết cho 2. Do đó 2 là một ước của 14.
Lại có: 6 . 2 = 12 và 6 . 3 = 18 nên 12 và 18 đều chia hết cho 6.
Do đó 12 và 18 là hai bội của 6.
Tương tự các em có thể lấy các ví dụ khác.
Câu 4:
a) Thực hiện các phép tính: 9 . 0; 9 . 1; 9 . 2; 9 . 3; 9 . 4; 9 . 5; 9 . 6.
b) Hãy chỉ ra bảy bội của 9.
 Xem đáp án
Xem đáp án
a) Ta có: 9 . 0 = 0; 9 . 1 = 9; 9 . 2 = 18; 9 . 3 = 27; 9 . 4 = 36; 9 . 5 = 45; 9 . 6 = 54.
b) Theo câu a, ta thấy các số 0; 9; 18; 27; 36; 45; 54 đều chia hết cho 9 nên bảy bội của 9 là: 0; 9; 18; 27; 36; 45; 54.
Câu 5:
a) Viết các bội nhỏ hơn 30 của 8.
b) Viết các bội có hai chữ số của 11.
 Xem đáp án
Xem đáp án
a) Để tìm các bội của 8, ta lần lượt nhân 8 với 0; 1; 2; 3; 4; …
Vì đề bài yêu cầu các bội của 8 nhỏ hơn 30 nên ta lần lượt nhân 8 với 0; 1; 2; 3 (vì 8.4 = 32 > 30).
Do đó: ta được các bội nhỏ hơn 30 của 8 là: 0; 8; 16; 24.
b) Để tìm các bội của 11 ta lần lượt lấy 11 nhân với 0; 1; 2; 3; ….
Đề bài yêu cầu tìm các bội có hai chữ số của 11 nên ta lần lượt lấy 11 nhân với 1; 2; 3; …; 9. (Vì 11. 0 = 0 là số có một chữ số và 11 . 10 = 110 là số có ba chữ số)
Vậy ta được các bội có hai chữ số của 11 là: 11; 22; 33; 44; 55; 66; 77; 88; 99.
Câu 6:
a) Tìm số thích hợp ở ?:
8 : 1 = ?; 8 : 5 = ? (dư ?);
8 : 2 = ?; 8 : 6 = ? (dư ?);
8 : 3 = ? (dư ?); 8 : 7 = ? (dư ?);
8 : 4 = ?; 8 : 8 = ?;
b) Hãy chỉ ra các ước của 8.
 Xem đáp án
Xem đáp án
a) Ta có:
8 : 1 = 8
8 : 2 = 4
8 : 3 = 2 (dư 2)
8 : 4 = 2
8 : 5 = 1 (dư 3)
8 : 6 = 1 (dư 2)
8 : 7 = 1 (dư 1)
8 : 8 = 1.
b) Theo câu a, ta có 8 chia hết cho các số 1; 2; 4; 8 nên các ước của 8 là: 1; 2; 4; 8.
Câu 7:
Tìm các ước của 25.
 Xem đáp án
Xem đáp án
Để tìm các ước của 25, ta lần lượt thực hiện phép chia số 25 cho các số tự nhiên từ 1 đến 25. Các phép chia hết là:
25 : 1 = 25; 25 : 5 = 5; 25 : 25 = 1.
Vậy các ước của 25 là 1; 5 và 25.
Câu 8:
Chỉ ra số thích hợp cho ? theo mẫu:

 Xem đáp án
Xem đáp án
+) Ta có: 6 . 2 = 12 và 6 . 6 = 36 nên 12 và 36 đều chia hết cho 6.
Khi đó: 12 + 36 = 48 = 6 . 8 nên 48 cũng chia hết cho 6.
+) Lại có: 9 . 5 = 45 và 9 . 7 = 63 nên 45 và 63 đều chia hết cho 9.
Khi đó 45 + 63 = 108 = 9 . 12 nên 108 cũng chia hết cho 9.
Vậy ta có thể điền vào bảng trên các số như sau:
|
m |
Số a chia hết cho m |
Số b chia hết cho m |
Thực hiện phép chia (a + b) cho m |
|
5 |
95 |
55 |
(95 + 55) : 5 = 30 |
|
6 |
12 |
36 |
(12 + 36) : 6 = 8 |
|
9 |
45 |
63 |
(45 + 63) : 9 = 12 |
Tương tự, các em có thể chọn số thích hợp tùy ý điền vào bảng.
Câu 9:
Không tính tổng, hãy giải thích tại sao A = 1 930 + 1 945 + 1 975 chia hết cho 5.
 Xem đáp án
Xem đáp án
Ta có:
1 930 : 5 = 386;
1 945 : 5 = 389;
1 975 : 5 = 395.
Do đó các số 1 930; 1 945 và 1 975 đều chia hết cho 5 nên theo tính chất chia hết của một tổng thì tổng A = 1 930 + 1 945 + 1 975 chia hết cho 5.
Câu 10:
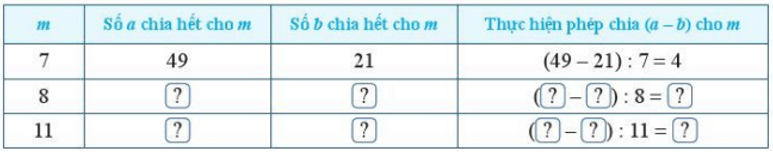
Chỉ ra số thích hợp cho ? theo mẫu:
 Xem đáp án
Xem đáp án
Ta có:
+) 8 . 7 = 56 và 8 . 2 = 16 nên các số 56 và 16 đều chia hết cho 8
Khi đó: 56 – 16 = 40 = 8 . 5 nên 40 chia hết cho 8.
+) 11 . 10 = 110 và 11 . 3 = 33 nên các số 110 và 33 đều chia hết cho 11
Khi đó: 110 – 33 = 77 = 11 . 7 nên 77 chia hết cho 11.
Vậy ta có thể điền các số vào bảng trên như sau:
|
m |
Số a chia hết cho m |
Số b chia hết cho m |
Thực hiện phép chia (a – b) cho m |
|
7 |
49 |
21 |
(49 – 21) : 7 = 4 |
|
8 |
56 |
16 |
(56 – 16) : 8 = 5 |
|
11 |
110 |
33 |
(110 – 33) : 11 = 7 |
Tương tự, các em có thể chọn số thích hợp tùy ý điền vào bảng
Câu 11:
Không tính hiệu, hãy giải thích tại sao A = 2 020 – 1 820 chia hết cho 20.
 Xem đáp án
Xem đáp án
Ta có:
2 020 : 20 = 101;
1 820 : 20 = 91;
Do đó các số 2 020 và 1 820 đều chia hết cho 20 nên theo tính chất chia hết của một hiệu ta có hiệu A = 2 020 – 1 820 chia hết cho 20.
Câu 12:
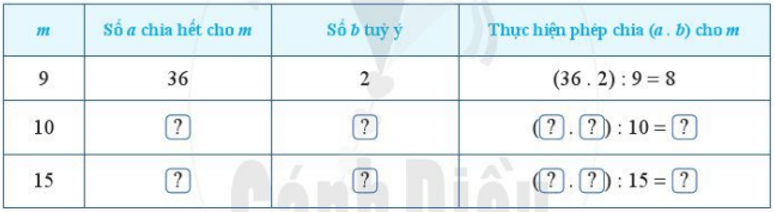
Chỉ ra số thích hợp cho ? theo mẫu:
 Xem đáp án
Xem đáp án
Ta có:
+) 10 . 10 = 100 nên 100 là số chia hết cho 10, lấy số 3 tùy ý, ta có:
100 . 3 = 300 = 10 . 30 nên 300 là số chia hết cho 10.
+) 15 . 5 = 75 nên 75 là số chia hết cho 15, lấy số 4 tùy ý, ta có:
75 . 4 = 300 = 15 . 20 nên 300 là số chia hết cho 15.
Vậy ta có thể điền các số vào bảng trên như sau:
|
m |
Số a chia hết cho m |
Số b tùy ý |
Thực hiện phép chia (a . b) cho m |
|
9 |
36 |
2 |
(36 . 2) : 9 = 8 |
|
10 |
100 |
3 |
(100 . 3) : 10 = 30 |
|
15 |
75 |
4 |
(75 . 4) : 15 = 20 |
Tương tự, các em có thể chọn số thích hợp tùy ý điền vào bảng.
Câu 13:
Không tính giá trị biểu thức, hãy giải thích tại sao A = 36 . 234 + 217 . 24 – 54 . 13 chia hết cho 6.
 Xem đáp án
Xem đáp án
Ta có: 36 : 6 = 6; 24 : 6 = 4; 54 : 6 = 9.
Nên các số 36; 24; 54 đều là các số chia hết cho 6, áp dụng tính chất chia hết của một tích ta có:
36 . 234; 217. 24; 54 . 13 đều là các tích chia hết cho 6.
Khi đó: A = 36 . 234 + 217 . 24 – 54 . 13 chia hết cho 6.
(Theo tính chất chia hết của một tổng và tính chất chia hết của một hiệu)
Câu 14:
Chỉ ra bốn bội của số m, biết:
a) m = 15;
b) m = 30;
c) m = 100.
 Xem đáp án
Xem đáp án
Vì một số tự nhiên khác 0 có vô số bội nên ta mỗi học sinh có thể chọn các bội khác nhau của số m tùy ý thích hợp. Ví dụ các em có thể làm như sau.
a) m = 15
Để tìm bốn bội của 15, ta lần lượt lấy 15 nhân với 0; 1; 2; 3
Vậy ta được bốn bội của 15 là: 0; 15; 30 và 45.
b) m = 30
Để tìm bốn bội của 30, ta lần lượt lấy 30 nhân với 0; 1; 2; 3
Vậy ta được bốn bội của 30 là: 0; 30; 60; 90.
c) m = 100
Để tìm bốn bội của 100, ta lần lượt lấy 100 nhân với 0; 1; 2; 3
Vậy ta được bốn bội của 100 là: 0; 100; 200; 300.
Tương tự cách làm trên, mỗi em học sinh có thể tìm được bốn bội khác nhau tùy ý thỏa mãn yêu cầu bài toán.
Câu 15:
Tìm tất cả các ước của số n, biết:
a) n = 13;
b) n = 20;
c) n = 26.
 Xem đáp án
Xem đáp án
a) n = 13
Để tìm các ước của số 13, ta lần lượt thực hiện phép chia số 13 cho các số tự nhiên từ 1 đến 13. Các phép chia hết là:
13 : 1 = 13; 13 : 13 = 1.
Vậy các ước của số 13 là 1 và 13.
b) n = 20
Để tìm các ước của số 20, ta lần lượt thực hiện phép chia số 20 cho các số tự nhiên từ 1 đến 20. Các phép chia hết là:
20 : 1 = 20; 20 : 2 = 10; 20 : 4 = 5; 20 : 5 = 4; 20 : 10 = 2; 20 : 20 = 1.
Vậy các ước của số 20 là: 1; 2; 4; 5; 10 và 20.
c) n = 26
Để tìm các ước của số 26, ta lần lượt thực hiện phép chia số 26 cho các số tự nhiên từ 1 đến 26. Các phép chia hết là:
26 : 1 = 26; 26 : 2 = 13; 26 : 13 = 2; 26 : 26 = 1.
Vậy các ước của số 26 là: 1; 2; 13 và 26.
Câu 16:
Tìm số tự nhiên x, biết x là bội của 9 và 20 < x < 40.
 Xem đáp án
Xem đáp án
Vì x là bội của 9 nên trước tiên, ta đi tìm các bội của 9, ta lần lượt lấy 9 nhân với 0; 1; 2; 3; 4; 5; …
Ta được các bội của 9 là: 0; 9; 18; 27; 36; 45; …
Mà 20 < x < 40
Vậy số tự nhiên x thỏa mãn yêu cầu bài toán là 27; 36.
Câu 17:
Đội Sao đỏ của trường có 24 bạn. Cô phụ trách muốn chia cả đội thành các nhóm đều nhau để kiểm tra vệ sinh lớp học, mỗi nhóm có ít nhất 2 bạn. Em hãy chia giúp cô giáo bằng các cách có thể.
 Xem đáp án
Xem đáp án
Vì các nhóm có số bạn đều nhau nên số bạn của mỗi nhóm phải là ước của 24.
Ta đi tìm các ước của số 24, ta thực hiện phép chia số 24 cho các số tự nhiên từ 1 đến 24. Các phép chia hết là:
24 : 1 = 24; 24 : 2 = 12; 24 : 3 = 8; 24 : 4 = 6; 24 : 6 = 4; 24 : 8 = 3; 24 : 12 = 2;
24 : 24 = 1.
Do đó các ước của 24 là 1; 2; 3; 4; 6; 8; 12; 24.
Vì mội đội có ít nhất hai bạn nên cô phụ trách có thể chia đội thành:
+ Nếu mỗi nhóm có 2 bạn thì số nhóm là: 24 : 2 = 12 (nhóm)
+ Nếu mỗi nhóm có 3 bạn thì số nhóm là: 24 : 3 = 8 (nhóm)
+ Nếu mỗi nhóm có 4 bạn thì số nhóm là: 24 : 4 = 6 (nhóm)
+ Nếu mỗi nhóm có 6 bạn thì số nhóm là: 24 : 6 = 4 (nhóm)
+ Nếu mỗi nhóm có 8 bạn thì số nhóm là: 24 : 8 = 3 (nhóm)
+ Nếu mỗi nhóm có 12 bạn thì số nhóm là: 24 : 12 = 2 (nhóm)
Một nhóm không thể có 24 bạn, vì 24 là tổng sổ bạn của cả đội Sao đỏ.
Vậy cô có thể chia đội thành:
+ 12 nhóm mỗi nhóm có 2 bạn;
+ 8 nhóm mỗi nhóm có 3 bạn;
+ 6 nhóm mỗi nhóm có 4 bạn;
+ 4 nhóm mỗi nhóm có 6 bạn;
+ 3 nhóm mỗi nhóm có 8 bạn;
+ 2 nhóm mỗi nhóm có 12 bạn.
Câu 18:
Hãy tìm đáp án đúng trong các đáp án A, B, C và D:
a) Nếu m ⁝ 4 và n ⁝ 4 thì m + n chia hết cho
A. 16.
B. 12.
C. 8.
D. 4.
b) Nếu m ⁝ 6 và n ⁝ 2 thì m + n chia hết cho
A. 6.
B. 4.
C. 3.
D. 2.
 Xem đáp án
Xem đáp án
a) Vì m ⁝ 4 và n ⁝ 4 thì m + n chia hết cho 4 (áp dụng tính chất chia hết của một tổng).
Do đó trong bốn đáp án đã cho, ta chọn đáp án D.
b) Ta có: 6 = 2 . 3
Mà m ⁝ 6 nên suy ra m ⁝ 2
Lại có n ⋮ 2
Do đó: m + n cũng chia hết cho 2 (tính chất chia hết của một tổng)
Do đó trong bốn đáp án đã cho, ta chọn đáp án D.
Câu 19:
Chỉ ra ba số tự nhiên m, n, p thỏa mãn các điều kiện sau: m không chia hết cho p và n không chia hết cho p nhưng m + n chia hết cho p.
 Xem đáp án
Xem đáp án
Ta có thể đưa ra nhiều bộ ba số thỏa mãn yêu cầu bài toán như sau:
+ Ví dụ 1. Các số 7; 9 và 2.
Ta có 7 không chia hết cho 2 và 9 cũng không chia hết cho 2 nhưng 7 + 9 = 16 lại chia hết cho 2.
+ Ví dụ 2. Các số 13; 19 và 4.
Ta có 13 không chia hết cho 4 và 19 cũng không chia hết cho 4 nhưng 13 + 19 = 32 lại chia hết cho 4.
+ Ví dụ 3. Các số 33; 67 và 10.
Ta có 33 không chia hết cho 10 và 67 cũng không chia hết cho 10 nhưng 33 + 67 = 100 lại chia hết cho 10.
Tương tự, các em có thể đưa ra các bộ ba số khác nhau thỏa mãn yêu cầu bài toán.
Qua bài tập 6 này, ta rút ra nhận xét như sau:
Nếu m chia hết cho p và n chia hết cho p thì tổng m + n chia hết cho p nhưng điều ngược lại chưa chắc đã đúng.
Nếu tổng m + n chia hết cho p thì chưa chắc m chia hết cho p và n chia hết cho p.
Câu 20:
Cho a và b là hai số tự nhiên . Giải thích tại sao nếu (a+b) ⁝ m và a ⁝ m thì b ⁝ m.
 Xem đáp án
Xem đáp án
Vì (a+b) ⁝ m nên ta có số tự nhiên k (k ≠ 0) thỏa mãn a + b = m.k (1)
Tương tự, vì a ⁝ m nên ta cũng có số tự nhiên h (h ≠ 0) thỏa mãn a = m.h
Thay a = m. h vào (1) ta được: m.h + b = m.k
Suy ra b = m.k – m.h = m.(k – h) (tính chất phân phối của phép nhân với phép trừ).
Mà m ⁝ m nên theo tính chất chia hết của một tích ta có m(k-h) ⁝ m.
Vậy b ⁝ m
Câu 21:
Một cửa hàng có hai loại khay nướng bánh. Loại khay thứ nhất chứa 3 chiếc bánh. Loại khay thứ hai chứa 6 chiếc bánh. Sau một số lần nướng bằng cả hai loại khay trên, người bán hàng đếm được số bánh làm ra là 125 chiếc. Hỏi người bán hàng đã đếm đúng hay sai số bánh làm được? Biết rằng mỗi lần nướng, các khay đều xếp đủ số bánh.
 Xem đáp án
Xem đáp án
Hai loại khay nướng bánh mỗi loại lần lượt chứa 3 chiếc bánh và 6 chiếc bánh.
Vì 3 chia hết cho 3 và 6 cũng chia hết cho 3 và mỗi lần nướng các khay đều được xếp đủ số bánh nên theo tính chất chia hết của một tích và một tổng thì tổng số bánh làm ra sau một số lần nướng bằng cả hai loại khay trên phải là số chia hết cho 3.
Mà 125 : 3 = 41 (dư 2) hay 125 không chia hết cho 3.
Vậy người bán hàng đã đếm sai số bánh làm được.
Câu 22:
Một đoàn khách du lịch đi tham quan chợ nổi Cái Răng ở TP. Cần Thơ bằng thuyền, mỗi thuyền chở 5 khách du lịch. Sau đó một số khách trong đoàn rời địa điểm tham quan trước bằng thuyền to hơn, mỗi thuyền chở 10 khách du lịch. Hướng dẫn viên kiểm đếm số khách du lịch còn lại là 21 người. Hỏi hết quả kiểm đếm trên là đúng hay sai?
 Xem đáp án
Xem đáp án
Ban đầu mỗi thuyền chở 5 khách du lịch nên tổng số khách phải là số chia hết cho 5.
Một số khách rời đi bằng thuyền chở 10 khách du lịch nên số khách rời đi chia hết cho 10 mà 10 = 5. 2 nên số khách rời đi phải chia hết cho 5.
Do đó số khách còn lại cũng phải chia hết cho 5 (theo tính chất chia hết của một hiệu).
Mà 21 : 5 = 4 (dư 1) hay 21 không chia hết cho 5.
Vậy kết quả kiểm đếm là sai.
