Bài 2: Đường kính và dây của đường tròn
-
4344 lượt thi
-
4 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hãy đưa ra một ví dụ để chứng tỏ rằng đường kính đi qua trung điểm của một dây có thể không vuông góc với dây ấy.
Xem đáp án
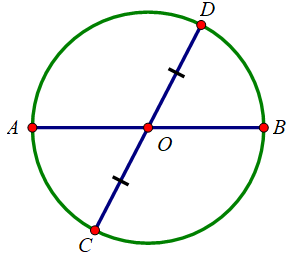
O là trung điểm của CD
AB đi qua trung điểm của CD nhưng AB không vuông góc với CD.
Câu 2:
Cho hình 67. Hãy tính độ dài dây AB, biết OA = 13 cm, AM = MB, OM = 5 cm.
Xem đáp án
OM là 1 phần đường kính đi qua trung điểm của AB
⇒ OM ⊥ AB
Xét tam giác OAM vuông tại M có:
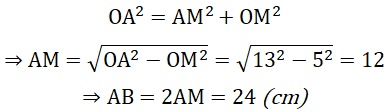
Câu 3:
Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE < BC.
Xem đáp án
a) Gọi M là trung điểm của BC.
=> MB = MC = BC
Tam giác BEC vuông tại E có EM là trung tuyến nên EM = BC
Tương tự tam giác vuông BCD có DM = BC
=> ME = MB = MC = MD
Do đó bốn điểm B, E, D, C cùng thuộc đường tròn tâm M. (đpcm)
b) Trong đường tròn tâm M nói trên, ta có DE là dây, BC là đường kính nên DE < BC.
Câu 4:
Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB, Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.
Gợi ý: Kẻ OM vuông góc với CD.
Xem đáp án
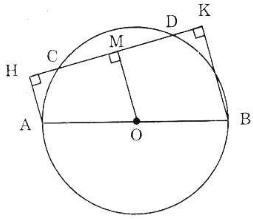
Kẻ OM ⊥ CD.
Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.
Hình thang AHKB có:
AO = OB (bán kính).
OM // AH // BK (cùng vuông góc HK)
=> OM là đường trung bình của hình thang.
=> MH = MK (1)
Vì OM ⊥ CD nên MC = MD (2)
Từ (1) và (2) suy ra CH = DK. (đpcm)