Chủ đề 2: Hệ thức giữa các cạnh và các góc của một tam giác vuông có đáp án
-
4490 lượt thi
-
6 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
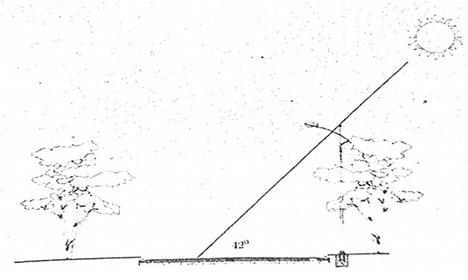
Một cột điện có bóng trên mặt đất dài 7,5m, các tia sáng mặt trời tạo với mặt đất một góc xấp xỉ 420. Tính chiều cao của cột đèn.
 Xem đáp án
Xem đáp án
Gọi chiều cao cột đèn là AB, bóng của nó trên mặt đất là AC.
Ta có .
Theo giả thiết, ta có .
Áp dụng tỉ số lượng giác trong tam giác ABC vuông ở A, ta có:
(cm).
Vậy chiều cao của cột đèn là 6,75 (cm).
Câu 2:
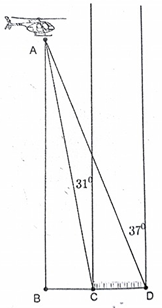
Ở độ cao 920m, từ một máy bay trực thăng người ta nhìn hai điểm D, C của hai đầu cầu những góc so với đường vuông góc với mặt đất các góc lần lượt là . Tính chiều dài CD của cây cầu (hình vẽ).
 Xem đáp án
Xem đáp án
Gọi A là vị trí của trực thăng, B là chân đường vuông góc hạ từ A xuống mặt đất. C và D là hai điểm đầu cầu.
Ta có
(m).
Mặt khác
(m).
Vậy chiều dài của cây cầu là:
(m).
Câu 3:
Cho tam giác ABC vuông ở A, đường cao AH. Tính ứng với mỗi trường hợp sau:
a) .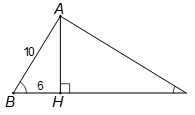
 Xem đáp án
Xem đáp án
Ta có: .
Vậy (cm).
Do đó .
Ta có: .
.
Vậy (cm).
Theo định lí Pythagore, ta có:
Suy ra (cm).
Vì vậy: .
Câu 4:
b) .
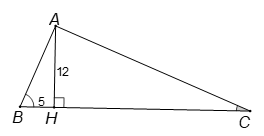
 Xem đáp án
Xem đáp án
Áp dụng định lí Pythagore trong tam giác vuông AHB vuông tại H, ta có:
.
Do đó (cm).
Suy ra: .
Ta có .
.
Vậy (cm).
Áp dụng định lí Pythagore trong tam giác AHC vuông tại H:
.
Vậy (cm).
Ta có: (cm).
Vậy: .
Câu 5:
Cho tam giác vuông ABC vuông ở A. Tính trong mỗi trường hợp sau:
a) ; Xem đáp án
Xem đáp án
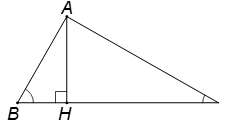
Ta có: .
Áp dụng công thức
, ta được:
Từ đó, ta có: (do sinB > 0)
Mặt khác, .Câu 6:
b) .
 Xem đáp án
Xem đáp án
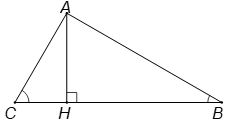
.
Ta có: .
Theo công thức lượng giác, ta được:
Từ đây, suy ra: (do sinB > 0).
