10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Ôn tập chương III - Đại số 9 có đáp án (Vận dụng)

Câu 1:

Điền số thích hợp vào chỗ trống

Giải hệ phương trình $\{\begin{cases} x + 4 y = 10 \\ y - z = 11 \\ z + \frac{x}{2} = - 6 \end{cases}$

Đáp số: Hệ phương trình có nghiệm duy nhất (x; y; z) = (…; …; …)

Xem đáp án

Ta xét hệ phương trình $\{\begin{cases} x + 4 y = 10 (1) \\ y - z = 11 (2) \\ z + \frac{x}{2} = - 6 (3) \end{cases}$

Từ phương trình (2), ta có: y = 11 + z (2’)

Từ phương trình (3), ta có: x = −12 – 2z (3’)

Thay y = 11 – z và x = −12 – 2z vào phương trình (1), ta có:

$- 12 - 2 z + 4 (11 + z) = 10 \Leftrightarrow 2 z = - 22 \Leftrightarrow z = - 11$

Thay z = −11 vào (2’), ta có y = 11 – 11 = 0

Thay z = −11 vào (3’), ta có x = −12 – 2.(−11) = 10

Vậy hệ phương trình đã cho có nghiệm duy nhất là (x; y; z) = (10; 0; −11)

Vậy số cần điền vào chỗ trống lần lượt là 10; 0; −11

Câu 2:

Lựa chọn đáp án đúng nhất

Giải hệ phương trình $\{\begin{cases} 2 (\frac{1}{x} + \frac{1}{2 y}) + 3 {(\frac{1}{x} - \frac{1}{2 y})}^{2} = 9 \\ \frac{1}{x} + \frac{1}{2 y} - 6 {(\frac{1}{x} - \frac{1}{2 y})}^{2} = - 3 \end{cases}$

Hệ phương trình có nghiệm là:

A. $(\frac{1}{4}; 1)$ và $(\frac{1}{2}; \frac{1}{2})$

B. $(1; \frac{1}{4})$ và $(- \frac{1}{2}; - \frac{1}{2})$

C. $(1; \frac{1}{4})$ và $(\frac{1}{2}; \frac{1}{2})$

D. $(1; \frac{1}{4})$ và $(\frac{3}{2}; \frac{1}{2})$

Xem đáp án

Điều kiện: $x, y \neq 0$

Đặt $u = \frac{1}{x} + \frac{1}{2 y}; v = {(\frac{1}{x} - \frac{1}{2 y})}^{2}$ , ta có hệ phương trình $\{\begin{cases} 2 u + 3 v = 9 \\ u - 6 v = - 3 \end{cases}$

$\Leftrightarrow \{\begin{cases} 4 u + 6 v = 18 \\ u - 6 v = - 3 \end{cases} \Leftrightarrow \{\begin{cases} 5 u = 15 \\ u - 6 v = - 3 \end{cases} \Leftrightarrow \{\begin{cases} u = 3 \\ v = 1 \end{cases}$

Suy ra

$\{\begin{cases} \frac{1}{x} + \frac{1}{2 y} = 3 \\ {(\frac{1}{x} - \frac{1}{2 y})}^{2} = 1 \end{cases} \Leftrightarrow \{\begin{cases} \frac{1}{x} + \frac{1}{2 y} = 3 \\ |\frac{1}{x} - \frac{1}{2 y}| = 1 \end{cases} \Leftrightarrow \{\begin{cases} \frac{1}{x} = 3 - \frac{1}{2 y} \\ |\frac{1}{x} - \frac{1}{2 y}| = 1 \end{cases} \Leftrightarrow \{\begin{cases} \frac{1}{x} = 3 - \frac{1}{2 y} \\ |3 - \frac{1}{2 y} - \frac{1}{2 y}| = 1 \end{cases}$

$\Leftrightarrow \{\begin{cases} \frac{1}{x} = 3 - \frac{1}{2 y} (1) \\ |3 - \frac{1}{y}| = 1 (2) \end{cases}$

$(2) \Leftrightarrow [\begin{array}{l} 3 - \frac{1}{y} = 1 \\ 3 - \frac{1}{y} = - 1 \end{array} \Leftrightarrow [\begin{array}{l} y = \frac{1}{2} \\ y = \frac{1}{4} \end{array} (T M)$

Thay $y = \frac{1}{2}$ vào (1), ta có $\frac{1}{x} = 2 \Leftrightarrow x = \frac{1}{2}$

Thay $y = \frac{1}{4}$ vào (1), ta có $\frac{1}{x} = 1 \Leftrightarrow x = 1$

Vậy hệ phương trình đã cho có hai nghiệm là $(1; \frac{1}{4})$ và $(\frac{1}{2}; \frac{1}{2})$

Đáp án cần chọn là: C

Câu 3:

Điền đáp án dạng (x; y) vào ô trống

Giải hệ phương trình $\{\begin{cases} |x + 1| + |y - 1| = 5 \\ |x + 1| = 4 y - 4 \end{cases}$

Đáp số: Hệ phương trình có hai nghiệm là: (…; …) và (…; …)

Xem đáp án

Từ phương trình thứ hai của hệ phương trình, ta có $4 y - 4 \geq 0$

Suy ra $y - 1 \geq 0 \Rightarrow |y - 1| = y - 1$

Khi đó hệ tương đương với hệ phương trình:

$\{\begin{cases} |x + 1| + y - 1 = 5 \\ |x + 1| = 4 y - 4 \end{cases}$ $\Leftrightarrow \{\begin{cases} |x + 1| + y = 6 \\ |x + 1| - 4 y = 4 \end{cases}$

Trừ từng vế phương trình thứ nhất cho từng vế phương trình thứ hai, ta có:

$\{\begin{cases} 5 y = 10 \\ |x + 1| - 4 y = 4 \end{cases} \Leftrightarrow \{\begin{cases} y = 2 \\ |x + 1| = 4 \end{cases} \Leftrightarrow \{\begin{cases} y = 2 \\ [\begin{array}{l} x + 1 = 4 \\ x + 1 = - 4 \end{array} \end{cases} \Leftrightarrow \{\begin{cases} y = 2 \\ [\begin{array}{l} x = 3 \\ x = - 5 \end{array} \end{cases}$

Vậy hệ phương trình có hai nghiệm là (3; 2) và (−5; 2)

Vậy cần điền vào ô trống để được đáp án đúng là (3; 2) và (−5; 2)

Câu 4:

Điền số thích hợp vào chỗ trống

Cho hệ phương trình $\{\begin{cases} m x + 2 y = m + 1 \\ 2 x + m y = 2 m - 1 \end{cases}$ .

Tìm các giá trị nguyên của m để hệ phương trình có nghiệm duy nhất là các số nguyên

Đáp số: $m \in \{...; ...; ...; ...\}$

Xem đáp án

Hướng dẫn

Bước 1: Tìm m để hệ có nghiệm duy nhất (x; y)

Bước 2: Giải hệ tìm nghiệm (x; y) theo tham số m. Viết x, y dưới dạng $a + \frac{k}{f (x)}$ trong đó a và k là số nguyên

Bước 3: Tìm m để x, y nguyên: f(m) là ước nguyên của k. So sánh với điều kiện ở bước 1 và kết luận

Lời giải

Từ phương trình thứ nhất, biểu diễn y theo x, ta được hệ phương trình:

$\{\begin{cases} y = \frac{1}{2} (- m x + m + 1) \\ 2 x + m y = 2 m - 1 \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{1}{2} (- m x + m + 1) \\ 2 x + \frac{1}{2} m (- m x + m + 1) = 2 m - 1 \end{cases}$

$\Leftrightarrow \{\begin{cases} y = \frac{1}{2} (- m x + m + 1) \\ 4 x - m^{2} x + m^{2} + m = 4 m - 2 \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{1}{2} (- m x + m + 1) \\ (4 - m^{2}) x + m^{2} - 3 m + 2 = 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} y = \frac{1}{2} (- m x + m + 1) \\ (m^{2} - 4) x = (m - 2) (m - 1) \end{cases} (*)$

Hệ đã cho có nghiệm duy nhất $\Leftrightarrow m^{2} - 4 \neq 0 \Leftrightarrow m \neq \pm 2$

Khi đó

$(*) \Leftrightarrow \{\begin{cases} y = \frac{1}{2} (- m x + m + 1) \\ x = \frac{m - 1}{m + 2} \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{2 m + 1}{m + 2} \\ x = \frac{m - 1}{m + 2} \end{cases} \Leftrightarrow \{\begin{cases} x = 1 - \frac{3}{m + 2} \\ y = 2 - \frac{3}{m + 2} \end{cases}$

Để x, y nguyên thì $\frac{3}{m + 2}$ nguyên. Suy ra m + 2 là ước nguyên của 3

Ta có bảng giá trị sau:

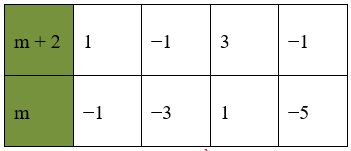
Các giá trị trên của m đều thỏa mãn

Vậy với $m \in \{\pm 1; - 3; - 5\}$ thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x; y nguyên

Vậy số cần điền vào chỗ trống là 1; −1; −3; −5

Câu 5:

Điền số thích hợp vào chỗ trống

Cho hệ phương trình $\{\begin{cases} x + m y = m + 1 \\ m x + y = 3 m - 1 \end{cases}$ . Tìm m để hệ có nghiệm duy nhất (x; y) sao cho tích xy nhỏ nhất

Đáp số: m = …

Xem đáp án

Hướng dẫn

Bước 1: Tìm m để hệ có nghiệm duy nhất (x; y)

Bước 2: Giải hệ tìm nghiệm (x; y) theo tham số m. Tính tích xy

Bước 3: Biến đổi tích xy về dạng A² + b rồi đánh giá tìm giá trị nhỏ nhất

Bước 4: Tìm m để dấu “=” xảy ra. So sánh với điều kiện ở bước 1 và kết luận

Lời giải

Biểu diễn x theo y từ phương trình thứ nhất của hệ, ta có:

$\{\begin{cases} x = - m y + m + 1 \\ m (- m y + m + 1) + y = 3 m - 1 \end{cases} \Leftrightarrow \{\begin{cases} x = - m y + m + 1 \\ - m^{2} y + m^{2} + m + y = 3 m - 1 \end{cases}$

$\Leftrightarrow \{\begin{cases} x = - m y + m + 1 \\ (m^{2} - 1) y = m^{2} - 2 m + 1 \end{cases} \Leftrightarrow \{\begin{cases} x = - m y + m + 1 \\ (m^{2} - 1) y = {(m - 1)}^{2} \end{cases} (*)$

Hệ có nghiệm duy nhất $\Leftrightarrow m^{2} - 1 \neq 0 \Leftrightarrow m \neq \pm 1$

Khi đó

$(*) \Leftrightarrow \{\begin{cases} x = - m y + m + 1 \\ y = \frac{m - 1}{m + 1} \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{3 m + 1}{m + 1} \\ y = \frac{m - 1}{m + 1} \end{cases}$

$S = x y = \frac{3 m + 1}{m + 1} . \frac{m - 1}{m + 1} = \frac{(3 m + 1) (m - 1)}{{(m + 1)}^{2}} = \frac{[3 (m + 1) - 2] . [(m + 1) - 2]}{{(m + 1)}^{2}}$

Đặt t = m + 1, ta có:

$S = \frac{(3 t - 2) (t - 2)}{t^{2}} = \frac{3 t^{2} - 8 t + 4}{t^{2}} = 3 - \frac{8}{t} + \frac{4}{t^{2}} = {(\frac{2}{t} - 2)}^{2} - 1$

Ta có ${(\frac{2}{t} - 2)}^{2} \geq 0 \Rightarrow S = {(\frac{2}{t} - 2)}^{2} - 1 \geq - 1$

Dấu “=” xảy ra khi $\frac{2}{t} - 2 = 0 \Leftrightarrow t = 1 \Leftrightarrow m + 1 = 1 \Leftrightarrow m = 0 (T M)$

Vậy m = 0 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn xy nhỏ nhất

Vậy số cần điền vào chỗ trống là 0

Câu 6:

Điền số thích hợp vào chỗ trống

Giải phương trình: $\sqrt{x + 1} + \sqrt[3]{x - 2} = 3$

Phương trình có nghiệm là x = …

Xem đáp án

Hướng dẫn

Bước 1: Tìm điều kiện xác định để phương trình có nghĩa

Bước 2: Đặt $u = \sqrt{x + 1}; v = \sqrt[3]{x - 2}$ . Lập hệ phương trình với hai ẩn u và v

Bước 3: Giải hệ phương trình, rồi thế trở lại để tìm x và y

Lời giải

Điều kiện xác định: $x \geq - 1$

Đặt $u = \sqrt{x + 1}; v = \sqrt[3]{x - 2}$ . Ta có u + v = 3 (theo phương trình ban đầu)

Lại có u² – v³ = 3

Ta có hệ phương trình: $\{\begin{cases} u + v = 3 \\ u^{2} - v^{3} = 3 \end{cases}$

$\Leftrightarrow \{\begin{cases} u = 3 - v \\ {(3 - v)}^{2} - v^{3} = 3 \end{cases} \Leftrightarrow \{\begin{cases} u = 3 - v \\ 9 - 6 v + v^{2} - v^{3} = 3 \end{cases} \Leftrightarrow \{\begin{cases} u = 3 - v \\ v^{3} - v^{2} + 6 v - 6 = 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} u = 3 - v \\ (v - 1) (v^{2} + 6) = 0 \end{cases} \Leftrightarrow \{\begin{cases} u = 3 - v \\ [\begin{array}{l} v^{2} - 6 = 0 (l o a i) \\ v - 1 = 0 \end{array} \end{cases} \Leftrightarrow \{\begin{cases} u = 2 \\ v = 1 \end{cases}$

Suy ra $\{\begin{cases} \sqrt{x + 1} = 2 \\ \sqrt[3]{x - 2} = 1 \end{cases} \Leftrightarrow \{\begin{cases} x + 1 = 4 \\ x - 2 = 1 \end{cases} \Leftrightarrow x = 3 (T M)$

Vậy phương trình có nghiệm duy nhất x = 3

Vậy số cần điền vào chỗ trống là 3

Câu 7:

Lựa chọn đáp án đúng nhất

Giải hệ phương trình $\{\begin{cases} x^{2} - y^{2} + 2 y = 1 \\ {(x + y)}^{2} - 2 x - 2 y = 0 \end{cases}$ . Hệ phương trình có nghiệm là:

A. $(\frac{1}{2}; - \frac{1}{2})$ và $(\frac{1}{2}; \frac{3}{2})$

B. $(- \frac{1}{2}; \frac{1}{2})$ và $(\frac{3}{2}; \frac{1}{2})$

C. $(- \frac{1}{2}; \frac{1}{2})$ và $(\frac{1}{2}; \frac{3}{2})$

D. $(- \frac{1}{2}; - \frac{1}{2})$ và $(\frac{1}{2}; \frac{3}{2})$

Xem đáp án

Ta có: $\{\begin{cases} x^{2} - y^{2} + 2 y = 1 (1) \\ {(x + y)}^{2} - 2 x - 2 y = 0 (2) \end{cases}$

$\begin{array}{l} (2) \Leftrightarrow {(x + y)}^{2} - 2 (x + y) = 0 \\ \Leftrightarrow (x + y) (x + y - 2) = 0 \\ \Leftrightarrow [\begin{array}{l} x + y = 0 \\ x + y - 2 = 0 \end{array} \end{array}$

Với x + y = 0, suy ra x = −y, thay vào phương trình (1), ta có:

${(- y)}^{2} - y^{2} + 2 y = 1 \Leftrightarrow 2 y = 1 \Leftrightarrow y = \frac{1}{2} \Rightarrow x = - \frac{1}{2}$

Với x + y = −2, suy ra x = 2 – y, thay vào phương trình (1), ta có:

${(2 - y)}^{2} - y^{2} + 2 y = 1 \Leftrightarrow (4 - 4 y + y^{2}) - y^{2} + 2 y = 1 \Leftrightarrow - 2 y = - 3 \Leftrightarrow y = \frac{3}{2} \Rightarrow x = \frac{1}{2}$

Vậy hệ phương trình đã cho có hai nghiệm là $(- \frac{1}{2}; \frac{1}{2})$ và $(\frac{1}{2}; \frac{3}{2})$

Đáp án cần chọn là: C

Câu 8:

Lựa chọn đáp án đúng nhất

Ba bạn học sinh vào cửa hàng mua đồ dùng học tập. Bạn thứ nhất mua 2 cái bút và 8 quyển vở hết 48000 đồng. Bạn thứ hai mua 5 quyển vở và 1 quyển sổ tay hết 22000 đồng. Bạn thứ ba mua 1 cái bút, 4 quyển vở và 2 quyển sổ tay hết 38000 đồng. Giá tiền mỗi cái bút, mỗi quyển vở và mỗi quyển sổ tay lần lượt là

A. 12000 đồng; 7000 đồng; 3000 đồng

B. 3000 đồng; 12000 đồng; 7000 đồng

C. 7000 đồng; 3000 đồng; 12000 đồng

D. 12000 đồng; 3000 đồng; 7000 đồng

Xem đáp án

Lời giải

Gọi x, y, z lần lượt là giá một cái bút, một quyển vở và một quyển sổ tay (đơn vị: đồng)

Bạn thứ nhất mua 2 cái bút và 8 quyển vở hết 48000 đồng nên ta có phương trình:

2x + 8y = 48000 (1)

Bạn thứ hai mua 5 quyển vở và 1 quyển sổ tay hết 22000 đồng nên ta có phương trình:

5y + z = 22000 (2)

Bạn thứ ba mua 1 cái bút, 4 quyển vở và 2 quyển sổ tay hết 38000 đồng nên ta có phương trình:

x + 4y + 2z = 38000 (3)

Từ (1), (2) và (3), ta có hệ phương trình $\{\begin{cases} 2 x + 4 y = 48000 (1) \\ 5 y + z = 22000 (2) \\ x + 4 y + 2 z = 38000 (3) \end{cases}$

Biểu diễn x và z theo y từ các phương trình (1) và (2), ta có:

x = 24000 – 4y; z = 22000 – 5y

Thay các giá trị này vào phương trình (3), ta có:

$(24000 - 4 y) + 4 y + 2 (22000 - 5 y) = 38000 \Leftrightarrow 10 y = 30000 \Leftrightarrow y = 3000$

Từ đó tìm được x = 12000; z = 7000

Vậy mỗi cái bút, mỗi quyển vở và mỗi quyển sổ tay lần lượt là 12000 đồng; 3000 đồng; 7000 đồng

Đáp án cần chọn là: D

Câu 9:

Điền số thích hợp vào chỗ trống

Con đường từ bản A đến trạm xá xã gồm một đoạn lên dốc dài 3 km, đoạn nằm ngang 12 km, đoạn xuống dốc 6 km. Một cán bộ đi xe máy từ bản A đến trạm xá hết 1 giờ 7 phút. Sau đó cán bộ này đi từ trạm xá trở về bản hết 1 giờ 16 phút. Hãy tính vận tốc của xe máy lúc lên dốc và lúc xuống dốc biết rằng trên đoạn đường nằm ngang, xe máy đi với vận tốc 18 km/h và vận tốc khi lên dốc, khi xuống dốc trong lúc đi và lúc về là như nhau.

Đáp số: Vận tốc lúc lên dốc là … km/h và vận tốc lúc xuống dốc là …km/h

Xem đáp án

Câu 10:

Điền số thích hợp vào chỗ trống

Điểm trung bình của 100 học sinh trong hai lớp 9A và 9B là 7,2. Tính điểm trung bình của các học sinh mỗi lớp biết rằng số học sinh lớp 9A gấp rưỡi số học sinh lớp 9B và điểm trung bình của học sinh lớp 9B gấp rưỡi điểm trung bình của lớp 9A.

Đáp số: Điểm trung bình của các học sinh lớp 9A là …

Điểm trung bình của các học sinh lớp 9B là …

Xem đáp án

Gọi số học sinh lớp 9A là a (học sinh) và số học sinh lớp 9B là b (học sinh)

Điều kiện: a, b nguyên dương

Do số học sinh lớp 9A gấp rưỡi số học sinh lớp 9B nên ta có:

$a = \frac{3}{2} b \Leftrightarrow \frac{a}{b} = \frac{3}{2} \Leftrightarrow \frac{a}{3} = \frac{b}{2} = \frac{a + b}{5} = \frac{100}{5} = 20$

Suy ra a = 3.20 = 60 và b = 20.2 = 40 (thỏa mãn)

Vậy số học sinh lớp 9A là 60 học sinh, số học sinh lớp 9B là 40 học sinh

Gọi điểm trung bình của các học sinh lớp 9A là x, điểm trung bình của các học sinh lớp 9B là y

Điều kiện: x, y > 0

Vì điểm trung bình của học sinh lớp 9B gấp rưỡi điểm trung bình của lớp 9A nên ta có y = 1,5x (1)

Điểm trung bình của các học sinh cả hai lớp là 7,2 nên ta có phương trình:

$\frac{60 x + 40 y}{100} = 7, 2 (2)$

Từ (1) và (2), ta có hệ phương trình: $\{\begin{cases} y = 1, 5 x \\ \frac{60 x + 40 y}{100} = 7, 2 \end{cases}$

$\Leftrightarrow \{\begin{cases} y = 1, 5 x \\ 60 x + 40.1, 5 x = 720 \end{cases} \Leftrightarrow \{\begin{cases} y = 1, 5 x \\ 120 x = 720 \end{cases} \Leftrightarrow \{\begin{cases} y = 9 \\ x = 6 \end{cases}$ (thỏa mãn)

Vậy: Điểm trung bình của các học sinh lớp 9A là 6,0

Điểm trung bình của các học sinh lớp 9B là 9,0

Vậy số cần điền vào chỗ trống lần lượt là 6,0 và 9,0

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Ôn tập chương III - Đại số 9 có đáp án

Trắc nghiệm Ôn tập chương III - Đại số 9 có đáp án (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương