Dạng 7. Bài luyện tập có đáp án
-
2886 lượt thi
-
59 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho nửa đường tròn đường kính BC = 2R. Từ điểm A trên nửa đường tròn vẽ AH vuông góc với BC Nửa đường tròn đường kính BH, CH lần lượt có tâm O1; O2 cắt AB, AC thứ tự tại D và E.
Chứng minh tứ giác ADHE là hình chữ nhật, từ đó tính DE biết R = 25 và BH = 10
 Xem đáp án
Xem đáp án
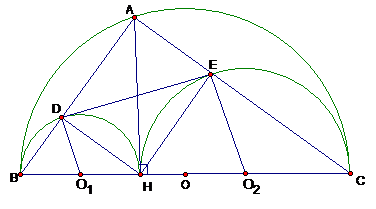
Ta có = 900 (vì góc nội tiếpchắn nửa đường tròn)
Tương tự có
Xét tứ giác ADHE có => ADHE là hình chữ nhật.
Từ đó DE = AH mà (Hệ thức lượng trong tam giác vuông)
hay (BH = 10; CH = 2.25 - 10 = 40) => DE = 20 (đơn vị độ dài)
Câu 2:
 Xem đáp án
Xem đáp án
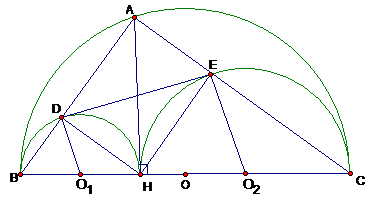
Ta có: (góc có cạnh tương ứng vuông góc) mà (1)
(Vì ADHE là hình chữ nhật) => do nên tứ giác BDEC nội tiếp đường tròn.
Câu 3:
 Xem đáp án
Xem đáp án
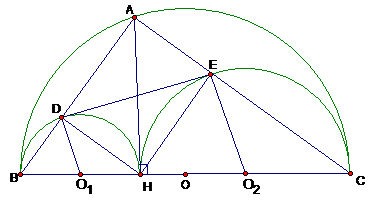
Vì => cân tại => (2)
Từ (1), (2) => = 900 =>
Vậy là hình thang vuông tại D và E.
Ta có S =
(Vì và )
Dấu "=" xảy ra khi và chỉ khi
là hình chữ nhật
A là điểm chính giữa cung BC Khi đó max .
Câu 4:
Cho đường tròn (O), đường kính AB, d1, d2 là các các đường thẳng lần lượt qua A, B và cùng vuông góc với đường thẳng AB. Lấy M, N là các điểm lần lượt thuộc d1, d2 sao cho = 900.
Chứng minh đường thẳng MN là tiếp tuyến của đường tròn (O).
 Xem đáp án
Xem đáp án
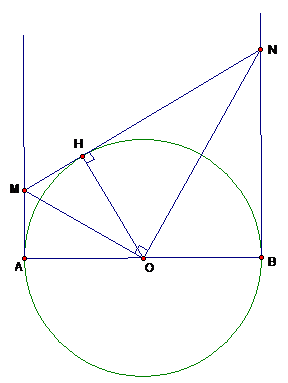
Gọi H là hình chiếu của O trên đường thẳng MN. Xét tứ giác OAMH
=> OAMH là tứ giác nội tiếp đường tròn.
Tương tự tứ giác OBNH nội tiếp được
=> (2 góc nội tiếp chắn 1 cung)
=> = 900. Hay H thuộc (O) lại có
=> MN là tiếp tuyến của (O)
Câu 5:
Chứng minh AM. BN =
 Xem đáp án
Xem đáp án
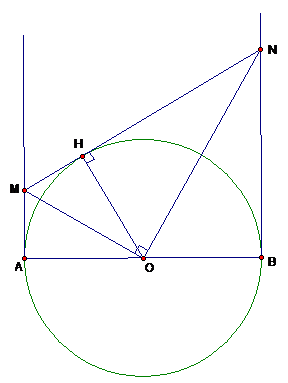
Ta có AM = MH, BN = NH, theo hệ thức lượng trong tam vuông, ta có:
(đpcm)
Câu 6:
Xác định vị trí của M, N để diện tích tam giác MON đạt giá trị nhỏ nhất.
 Xem đáp án
Xem đáp án

OH. MN > OH. AB (Vì AMNB là hình thang vuông)
Dấu “=” khi và chỉ khi MN = AB hay H là điểm chính giữa của cung AB
M, N song song với AB AM = BN =
Vậy nhỏ nhất khi và chỉ khi AM = BN =
Câu 7:
Cho ABC có 3 góc nhọn, trực tâm là H và nội tiếp đường tròn (O). Vẽ đường kính AK.
Chứng minh tứ giác BHCK là hình hình hành.
 Xem đáp án
Xem đáp án
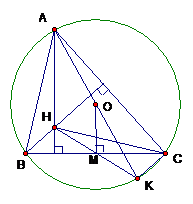
Ta có (vì góc nội tiếp chắn nửa đường tròn)
Nên CK vuông góc với AC mà BH vuông góc với AC (vì H trực tâm)
=> CK // BH tương tự có CH // BK
=> Tứ giác BHCK là hbh (đpcm)
Câu 8:
 Xem đáp án
Xem đáp án
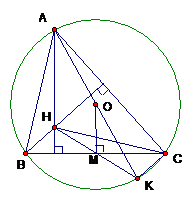
OM vuông góc với BC => M trung điểm của BC
(định lý đường kính và dây cung) => M là trung điểm của HK (vì BHCK là hình bình hành) => đpcm tam giác AHK có OM là đường trung bình => AH = 2.OM
Câu 9:
Gọi A’, B’, C’ là chân các đường cao thuộc các cạnh BC, CA, AB của tam giác ABC. Khi BC cố định hãy xác định vị trí điểm A để tổng S = A’B’ + B’C’ + C’A’ đạt giá trị lớn nhất.
 Xem đáp án
Xem đáp án
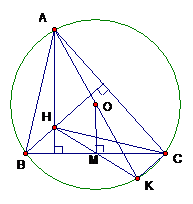
Ta có = 900=> tứ giác BC’B’C nội tiếp đường tròn => = mà (Ax là tiếp tuyến tại A) => Ax // B’C’
OA vuông góc với Ax => OA vuông góc với B’C’. Do đó SAB’OC’ = R.B’C’
Tương tự: SBA’OC’ = R.A’C’; SCB’OA’ = R.A’B’
= R(A’B’ + B’C’ + C’A’)= AA’.BC < (AO + OM).BC
A’B’ + B’C’ + C’A’, lớn nhất khi A, O, M thẳng hàng
A là điểm chính giữa cung lớn BC
Câu 10:
Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI = AO. Kẻ dây MN vuông góc với AB tại I, gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và B. Nối AC cắt MN tại E.
Chứng minh tứ giác IECB nội tiếp.
 Xem đáp án
Xem đáp án
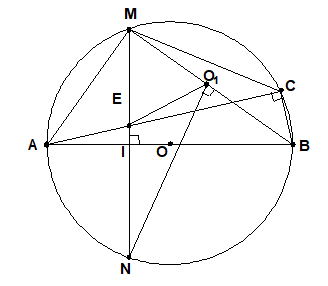
Theo giả thiết MN ^AB tại I
mà đây là hai góc đối của tứ giác IECB nên tứ giác IECB là tứ giác nội tiếp.
Câu 11:
Chứng minh hệ thức:
 Xem đáp án
Xem đáp án
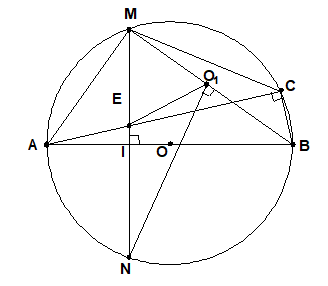
Theo giả thiêt MN ^AB, suy ra A là điểm chính giữa của nên (hai góc nội tiếp chắn hai cung bằng nhau) hay , lại có là góc chung do đó tam giác AME đồng dạng với tam giác ACM
C2:
Câu 12:
Hãy xác định vị trí của điểm C sao cho khoảng cách từ N đến tâm đường tròn ngoại tiếp tam giác CME là nhỏ nhất.
 Xem đáp án
Xem đáp án
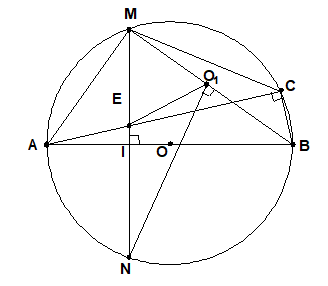
Theo trên AM là tiếp tuyến của đường tròn ngoại tiếp DECM. Nối MB ta có , do đó tâm O1 của đường tròn ngoại tiếp DECM phải nằm trên BM.
Ta thấy nhỏ nhất khi là khoảng cách từ N đến BM ^BM. Gọi O1 là chân đường vuông góc kẻ từ N đến BM ta được O1 là tâm đường tròn ngoại tiếp D ECM có bán kính là O1M.
Do đó để khoảng cách từ N đến tâm đường tròn ngoại tiếp D ECM là nhỏ nhất thì C phải là giao điểm của đường tròn (O1), bán kính O1M với đường tròn (O) trong đó O1 là hình chiếu vuông góc của N trên BM.
Câu 13:
Cho đường tròn ( O; R ) và điểm A nằm ngoài đường tròn sao cho . Từ A vẽ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Lấy D thuộc AB; E thuộc AC sao cho chu vi của tam giác ADE bằng 2R.
Chứng minh tứ giác ABOC là hình vuông.
 Xem đáp án
Xem đáp án
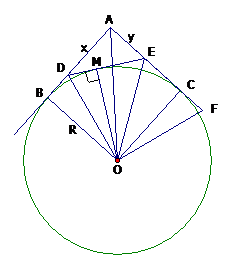
Ta có: (tính chất tiếp tuyến) (1)
AB = AC R = OB = OC (2).
Từ (1) và (2) suy ra ABOC là hình vuông.
Câu 14:
Chứng minh DE là tiếp tuyến của đường tròn (O; R).
 Xem đáp án
Xem đáp án
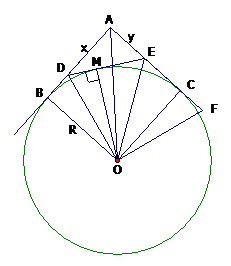
Theo bài ra ta có: AD + DE + AE = 2R (3).
Suy ra: DE = BD + CE (4).
Vẽ OM vuông góc với DE (M thuộc DE) (5)
Trên tia đối của tia CA lấy điểm F sao cho CF = BD; suy ra ∆BDO = ∆COF (c-g-c)
OD = OF; lại có DE = FE nên ∆ODE = ∆OFE (c-c-c)
OM = OC = R (hai đường cao tương ứng) (6).
Từ (5) và (6) suy ra DE là tiếp tuyến của đường tròn (O;R).
Câu 15:
Tìm giá trị lớn nhất của diện tích ∆ADE.
 Xem đáp án
Xem đáp án
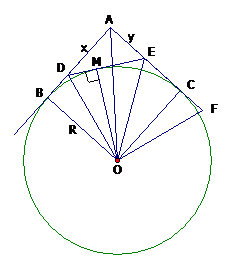
Đặt: AD = x; AE = y (x, y > 0)
Ta có: DE (định lí Pitago).
Vì AD + DE + AE = 2R = 2R (6)
Áp dụng BĐT – Côsi cho hai số không âm ta có: (7).
Dấu “=” xảy ra khi và chỉ khi x = y.
Từ (6) và (7) suy ra:
xy SADE .
Vậy max SADE = x = y ∆ADE cân tại A
Câu 16:
Cho đường trong (O, R) và đường thẳng d không qua O cắt đường tròn tại hai điểm A, B Lấy một điểm M trên tia đối của tia BA kẻ hai tiếp tuyến MC, MD với đường tròn (C, D là các tiếp điểm). Gọi H là trung điểm của AB
Chứng minh rằng các điểm M, D, O, H cùng nằm trên một đường tròn.
 Xem đáp án
Xem đáp án
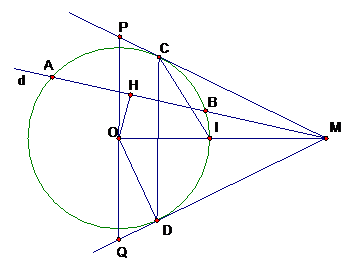
Vì H là trung điểm của AB nên hay . Theo tính chất của tiếp tuyến ta lại có hay . Suy ra các điểm M, D, O, H cùng nằm trên một đường tròn.
Câu 17:
Đoạn OM cắt đường tròn tại I. Chứng minh rằng I là tâm đường tròn nội tiếp tam giác MCD
 Xem đáp án
Xem đáp án
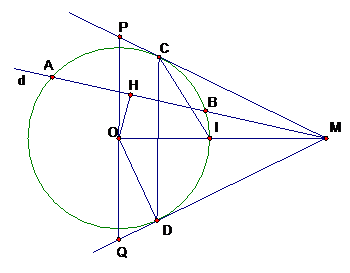
Theo tính chất tiếp tuyến, ta có MC = MD DMCD cân tại MMI là một đường phân giác của .
Mặt khác I là điểm chính giữa cung nhỏ nên sđ = sđ
CI là phân giác của . Vậy I là tâm đường tròn nội tiếp tam giác MCD
Câu 18:
Đường thẳng qua O, vuông góc với OM cắt các tia MC, MD thứ tự tại P và Q. Tìm vị trí của điểm M trên d sao cho diện tích tam giác MPQ bé nhất.
 Xem đáp án
Xem đáp án

Ta có tam giác MPQ cân ở M, có MO là đường cao nên diện tích của nó được tính: . Từ đó S nhỏ nhất MD + DQ nhỏ nhất. Mặt khác, theo hệ thức lượng trong tam giác vuông OMQ ta có không đổi nên MD + DQ nhỏ nhất DM = DQ = R. Khi đó OM = hay M là giao điểm của d với đường tròn tâm O bán kính .
Câu 19:
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ AC, AD thứ tự là đường kính của hai đường tròn (O) và Chứng minh ba điểm C, B, D thẳng hàng.
 Xem đáp án
Xem đáp án
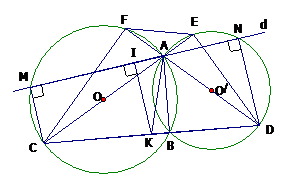
Ta có và lần lượt là các góc nội tiếp chắn nửa đường tròn (O) và (O’)
Suy ra C, B, D thẳng hàng.
Câu 20:
Đường thẳng AC cắt đường tròn tại E; đường thẳng AD cắt đường tròn (O) tại F (E, F khác A). Chứng minh 4 điểm C, D, E, F cùng nằm trên một đường tròn.
 Xem đáp án
Xem đáp án
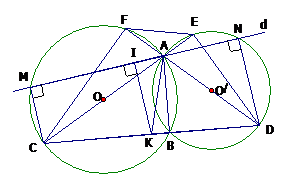
Xét tứ giác CDEF có:
(góc nội tiếp chắn nửa đường tròn (O))
(góc nội tiếp chắn nửa đường tròn (O’)
suy ra CDEF là tứ giác nội tiếp.
Câu 21:
Một đường thẳng d thay đổi luôn đi qua A cắt (O) và thứ tự tại M và N. Xác định vị trí của d để CM + DN đạt giá trị lớn nhất.
 Xem đáp án
Xem đáp án
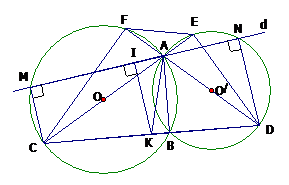
Ta có (góc nội tiếp chắn nửa đường tròn); suy ra CM // DN hay CMND là hình thang.
Gọi I, K thứ tự là trung điểm của MN và CD Khi đó IK là đường trung bình của hình thang CMND Suy ra IK // CM // DN (1) và CM + DN = 2.IK (2)
Từ (1) suy ra IK vuông góc MN IK KA (3) (KA là hằng số do A và K cố định).
Từ (2) và (3) suy ra: CM + DN 2KA
Dấu “ = ” xảy ra khi và chỉ khi IK = AK d vuông góc AK tại A
Vậy khi đường thẳng d vuông góc AK tại A thì (CM + DN) đạt giá trị lớn nhất bằng 2KA
Câu 22:
Từ một điểm A nằm ngoài đường tròn (O;R) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M, vẽ MI AB, MK AC (I AB,K AC)
Chứng minh: AIMK là tứ giác nội tiếp đường tròn.
 Xem đáp án
Xem đáp án
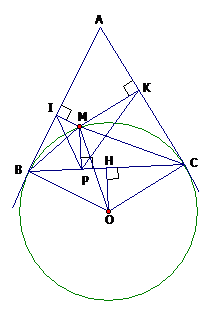
Ta có: (gt), suy ra tứ giác AIMK nội tiếp đường tròn đường kính AM.
Câu 23:
Vẽ MP vuông góc BC (P thuộc BC). Chứng minh: .
 Xem đáp án
Xem đáp án
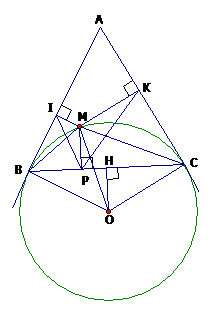
Tứ giác CPMK có (gt). Do đó CPMK là tứ giác nội tiếp (1). Vì KC là tiếp tuyến của (O) nên ta có: (cùng chắn ) (2). Từ (1) và (2) suy ra (3)
Câu 24:
Xác định vị trí của điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị lớn nhất.
 Xem đáp án
Xem đáp án
Chứng minh tương tự câu b ta có BPMI là tứ giác nội tiếp.
Suy ra: (4). Từ (3) và (4) suy ra .
Tương tự ta chứng minh được .
Suy ra: MPK ∆MIP
MI.MK = MP2 MI.MK.MP = MP3.
Do đó MI.MK.MP lớn nhất khi và chỉ khi MP lớn nhất (4)
- Gọi H là hình chiếu của O trên BC, suy ra OH là hằng số (do BC cố định).
Lại có: MP + OH OM = R MP R – OH. Do đó MP lớn nhất bằng R – OH khi và chỉ khi O, H, M thẳng hàng hay M nằm chính giữa cung nhỏ BC (5).
Từ (4) và (5) suy ra max (MI.MK.MP) = ( R – OH )3 M nằm chính giữa cung nhỏ BC
Câu 25:
Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt ở C và D. Các đường thẳng AD và BC cắt nhau tại N.
Chứng minh AC + BD = CD
 Xem đáp án
Xem đáp án
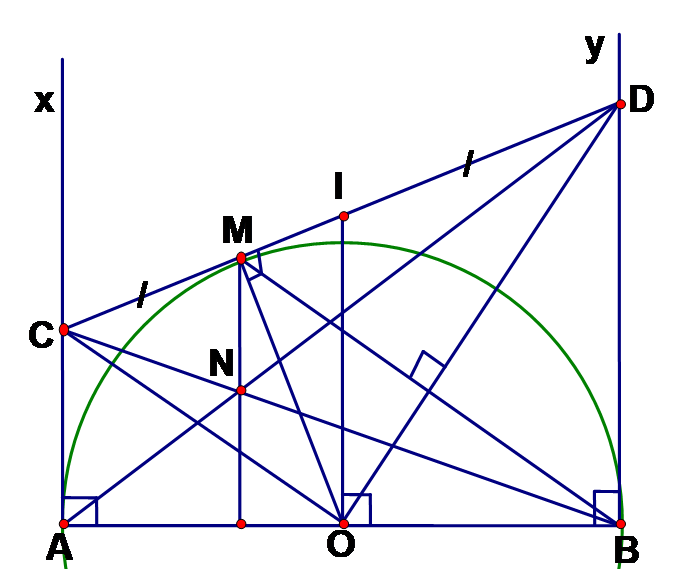
Theo tính chất hai tiếp tuyến cắt nhau ta có: CA = CM; DB = DM
=> AC + BD = CM + DM.
Mà CM + DM = CD => AC + BD = CD
Câu 26:
Chứng minh .
 Xem đáp án
Xem đáp án
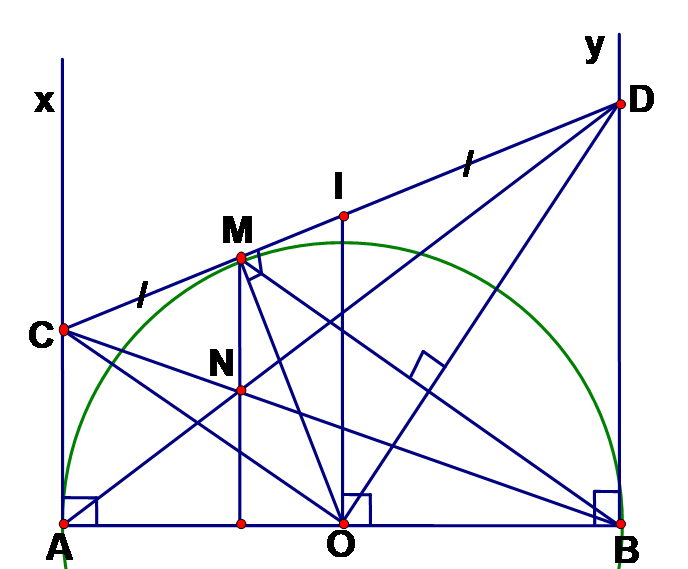
Theo tính chất hai tiếp tuyến cắt nhau ta có: OC là tia phân giác của góc AOM; OD là tia phân giác của góc BOM, mà và là hai góc kề bù => = 900.
Câu 27:
Chứng minh .
 Xem đáp án
Xem đáp án
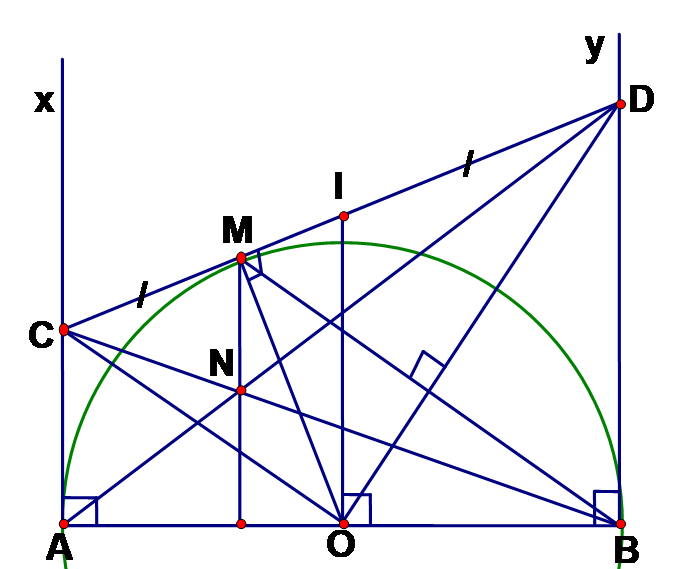
Theo trên nên tam giác COD vuông tại O có OM CD ( OM là tiếp tuyến ).
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có ,
Mà OM = R; CA = CM; DB = DM => =>
Câu 28:
Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt ở C và D Các đường thẳng AD và BC cắt nhau tại N.
Chứng minh OC // BM
 Xem đáp án
Xem đáp án
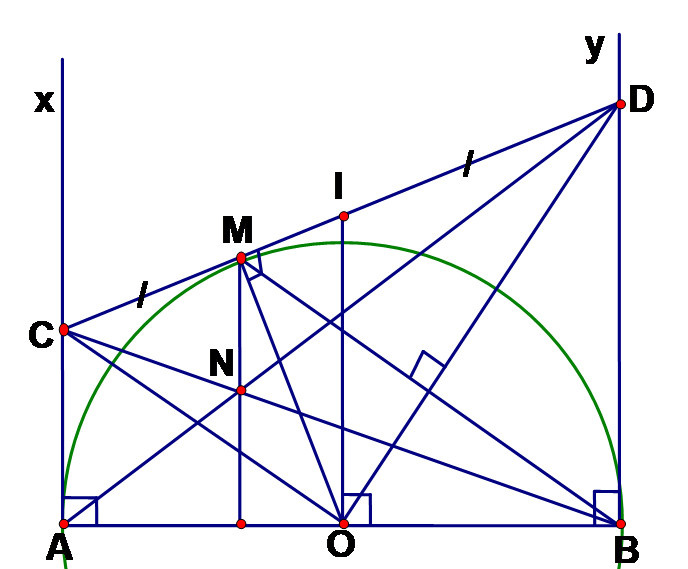
Theo trên nên OC ^ OD(1)
Theo tính chất hai tiếp tuyến cắt nhau ta có: DB = DM; lại có OM = OB =R => OD là trung trực của BM => BM ^ OD(2). Từ (1) Và (2) => OC // BM ( Vì cùng vuông góc với OD).
Câu 29:
Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt ở C và D Các đường thẳng AD và BC cắt nhau tại N.
Chứng minh AB là tiếp tuyến của đường tròn đường kính CD
 Xem đáp án
Xem đáp án

Gọi I là trung điểm của CD ta có I là tâm đường tròn ngoại tiếp tam giác COD đường kính CD có IO là bán kính.
Theo tính chất tiếp tuyến ta có AC ^ AB; BD ^ AB => AC // BD => tứ giác ACDB là hình thang. Lại có I là trung điểm của CD; O là trung điểm của AB => IO là đường trung bình của hình thang ACDB
IO // AC, mà AC ^ AB => IO ^ AB tại O => AB là tiếp tuyến tại O của đường tròn đường kính CD
Câu 30:
Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt ở C và D Các đường thẳng AD và BC cắt nhau tại N.
Chứng minh MN ^ AB
 Xem đáp án
Xem đáp án
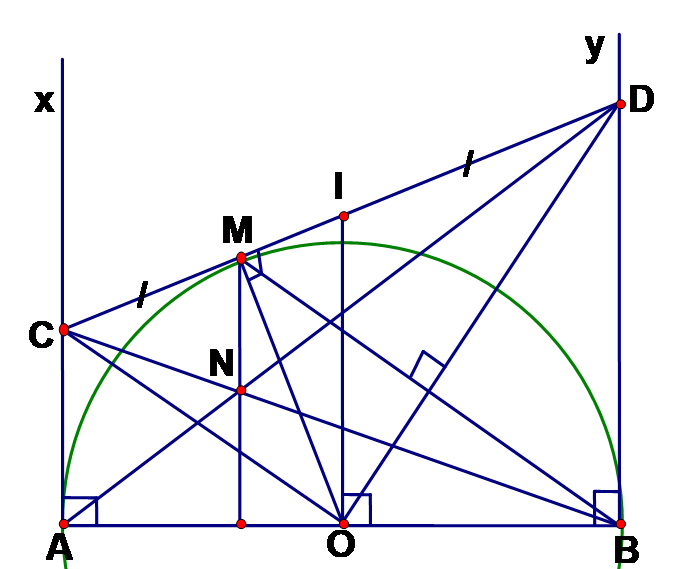
Theo trên AC // BD => , mà CA = CM; DB = DM nên suy ra => MN // BD mà BD ^ AB => MN ^ AB
Câu 31:
Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt ở C và D Các đường thẳng AD và BC cắt nhau tại N.
 Xem đáp án
Xem đáp án
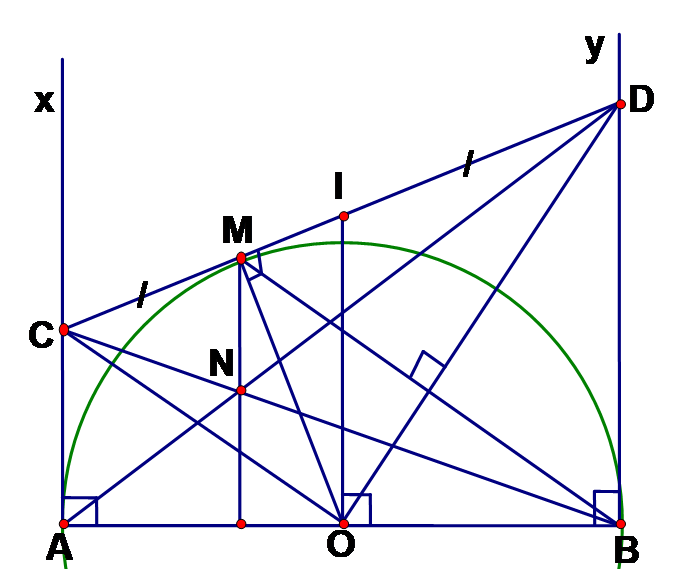
Ta có chu vi tứ giác ACDB = AB + AC + CD + BD mà AC + BD = CD nên suy ra chu vi tứ giác ACDB = AB + 2CD mà AB không đổi nên chu vi tứ giác ACDB nhỏ nhất khi CD nhỏ nhất, mà CD nhỏ nhất khi CD là khoảng cách giữ Ax và By tức là CD vuông góc với Ax và By. Khi đó CD // AB => M phải là trung điểm của cung AB.
Câu 32:
 Xem đáp án
Xem đáp án
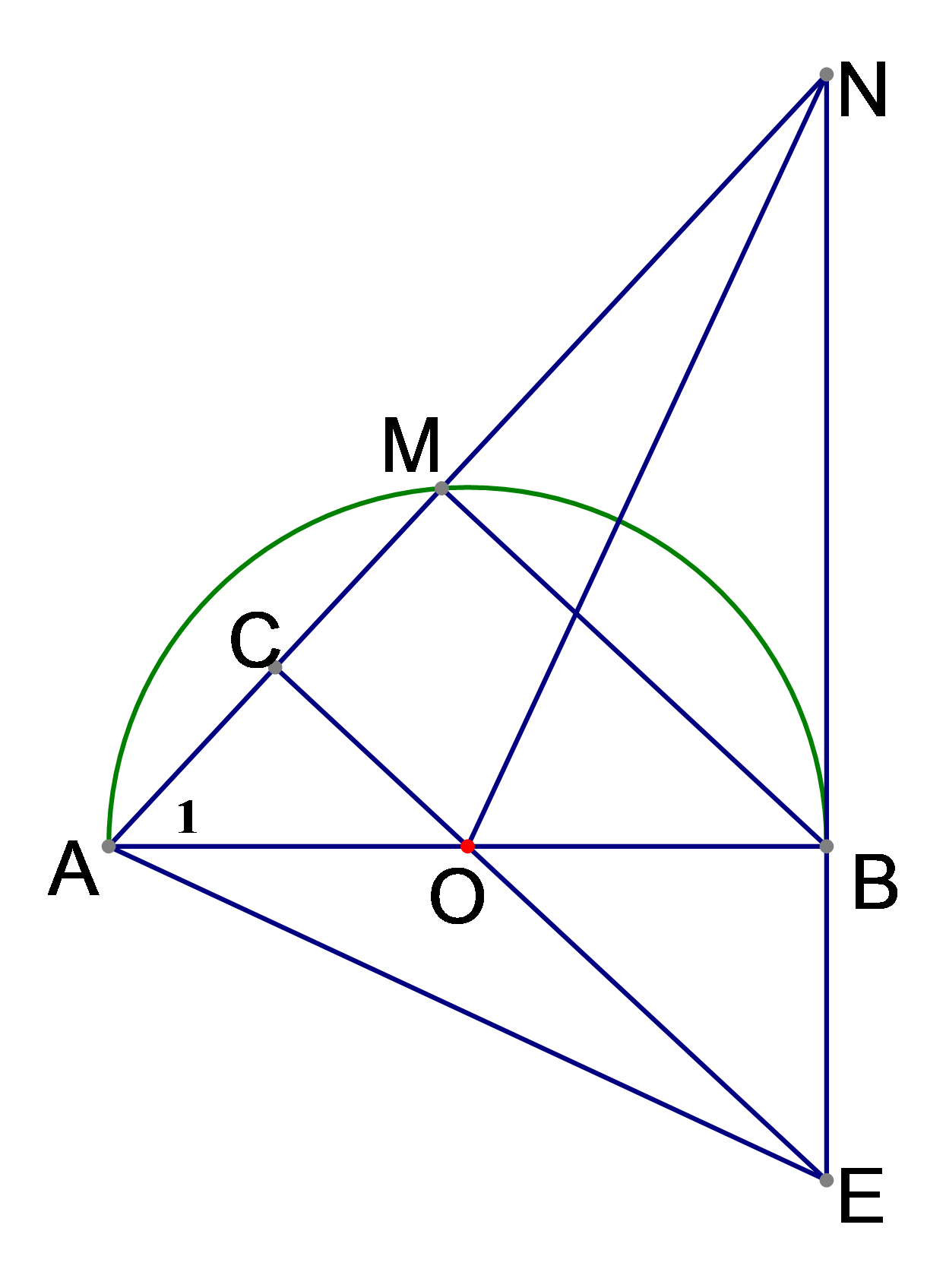
Phần đường kính OC đi qua trung điểm C của AM Þ OC ^ AM Þ .
BN là tiếp tuyến của (O) tại B Þ OB ^ BN Þ
Xét tứ giác OCNB có tổng hai góc đối:
Do đó tứ giác OCNB nội tiếp.
Câu 33:
Cho nửa đường tròn tâm O đường kính . Điểm M di chuyển trên nửa đường tròn (M khác A và B). C là trung điểm của dây cung AM. Đường thẳng d là tiếp tuyến với nửa đường tròn tại B Tia AM cắt d tại điểm N. Đường thẳng OC cắt d tại E.
Chứng minh: AC.AN = AO.AB
 Xem đáp án
Xem đáp án

Xét DACO và DABN có: chung;
Þ DACO ~ DABN (g.g)
Þ
Do đó ACAN = AO.AB (đpcm).
Câu 34:
Cho nửa đường tròn tâm O đường kính . Điểm M di chuyển trên nửa đường tròn (M khác A và B). C là trung điểm của dây cung AM. Đường thẳng d là tiếp tuyến với nửa đường tròn tại B Tia AM cắt d tại điểm N. Đường thẳng OC cắt d tại E.
Chứng minh: NO vuông góc với AE.
 Xem đáp án
Xem đáp án
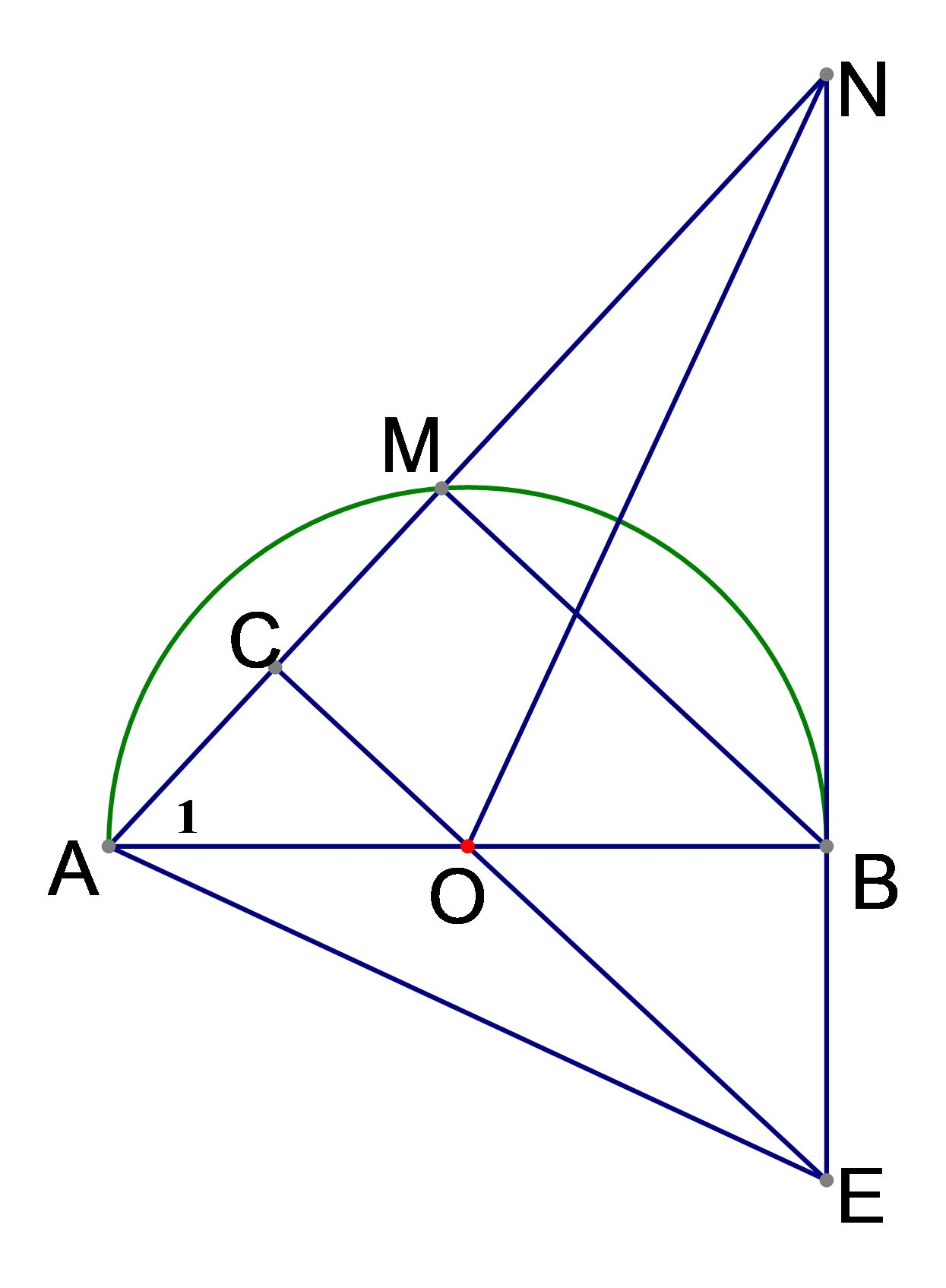
Theo chứng minh trên, ta có:
OC ^ AM Þ EC ^ AN Þ EC là đường cao của DANE (1)
OB ^ BN Þ AB ^ NE Þ AB là đường cao của DAME (2)
Từ (1) và (2) suy ra O là trực tâm của DANE (vì O là giao điểm của AB và EC).
Þ NO là đường cao thứ ba của DANE.
Do đó; NO ^ AE (đpcm).
Câu 35:
Cho nửa đường tròn tâm O đường kính . Điểm M di chuyển trên nửa đường tròn (M khác A và B). C là trung điểm của dây cung AM. Đường thẳng d là tiếp tuyến với nửa đường tròn tại B Tia AM cắt d tại điểm N. Đường thẳng OC cắt d tại E.
Tìm vị trí điểm M sao cho (2.AM + AN) nhỏ nhất.
 Xem đáp án
Xem đáp án
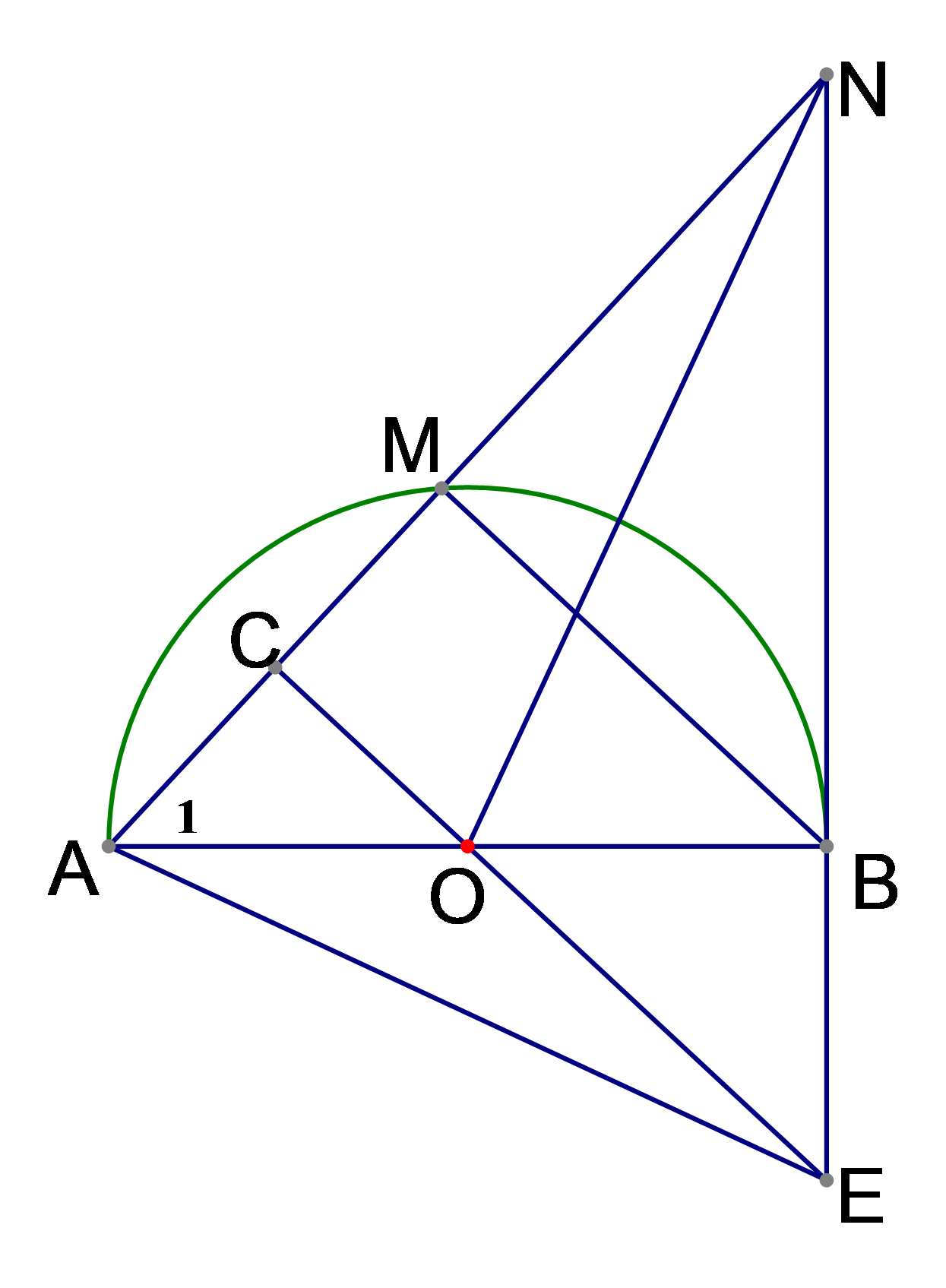
Ta có: 2.AM + AN = 4AC + AN (vì C là trung điểm của AM).
4AC.AN = 4AO.AB = 4R.2R = 8R2
Áp dụng bất đẳng thức Cô-si cho hai số dương, ta có:
4AC + AN ³
Þ Tổng 2.AM + AN nhỏ nhất = Û 4AC = AN
Û AN = 2AM Û M là trung điểm của AN.
DABN vuông tại B có BM là đường trung tuyến nên AM = MB
Þ Þ M là điểm chính giữa nửa đường tròn đường kính AB
Vậy với M là điểm chính giữa nửa đường tròn đường kính AB thì (2.AM + AN) nhỏ nhất = .
Câu 36:
Cho đường tròn (O) đường kính AB cố định và đường kính CD thay đổi không trùng với AB Tiếp tuyến tại A của đường tròn (O) cắt các đường thẳng BC và BD lần lượt tại E và F. Gọi P và Q lần lượt là trung điểm của các đoạn thẳng AE và AF.
Chứng minh ACBD là hình chữ nhật;
 Xem đáp án
Xem đáp án
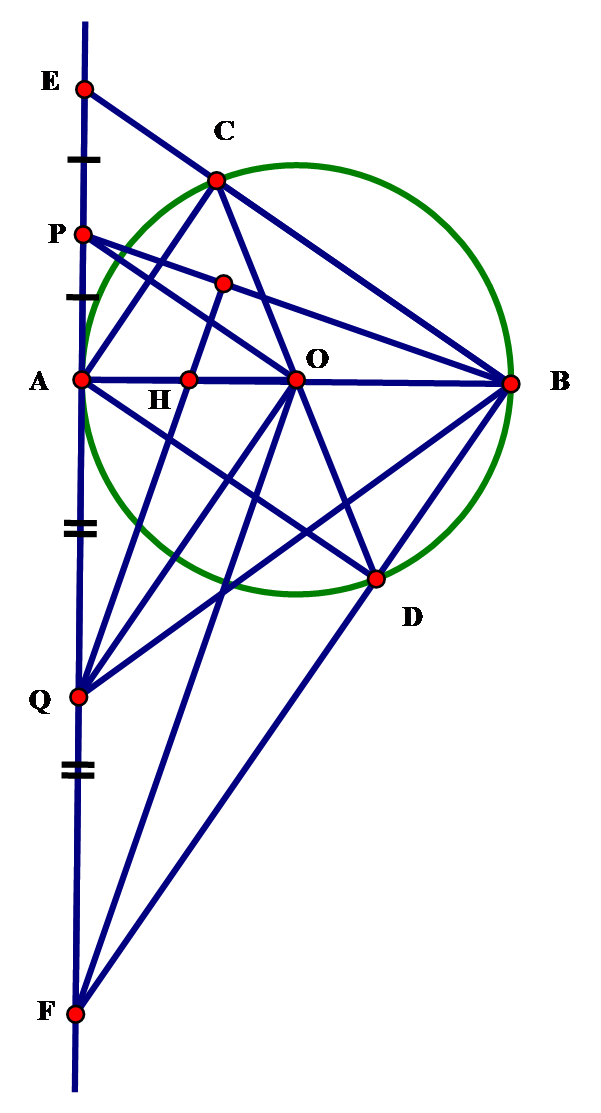
Có ( Các góc nội tiếp chắn nửa đường tròn)
Tứ giác ACBD là hình chữ nhật ( Tứ giác có ba góc vuông)
Câu 37:
Cho đường tròn (O) đường kính AB cố định và đường kính CD thay đổi không trùng với AB Tiếp tuyến tại A của đường tròn (O) cắt các đường thẳng BC và BD lần lượt tại E và F. Gọi P và Q lần lượt là trung điểm của các đoạn thẳng AE và AF.
 Xem đáp án
Xem đáp án

Có PO là đường trung bình của tam giác AEB PO // EB mà EB BF PO BF
Xét tam giác PBF có BA PF; PO BF nên BA và PO là các đường cao của tam giác PBF mà BA và PO căt nhau tại O nên O là trực tâm của tam giác PBF FO là đường cao thứ ba của tam giác PBF hay FO PB (1).
Lại có H là trực tâm của tam giác PBQ nên QH PB (2)Từ (1) và (2) QH // FO. Xét tam giác AOF có Q là trung điểm của AF; QH // FO nên H là trung điểm của AO
Câu 38:
Cho đường tròn (O) đường kính AB cố định và đường kính CD thay đổi không trùng với AB Tiếp tuyến tại A của đường tròn (O) cắt các đường thẳng BC và BD lần lượt tại E và F. Gọi P và Q lần lượt là trung điểm của các đoạn thẳng AE và AF.
Xác định vị trí của đường kính CD để tam giác BPQ có diện tích nhỏ nhất.
 Xem đáp án
Xem đáp án
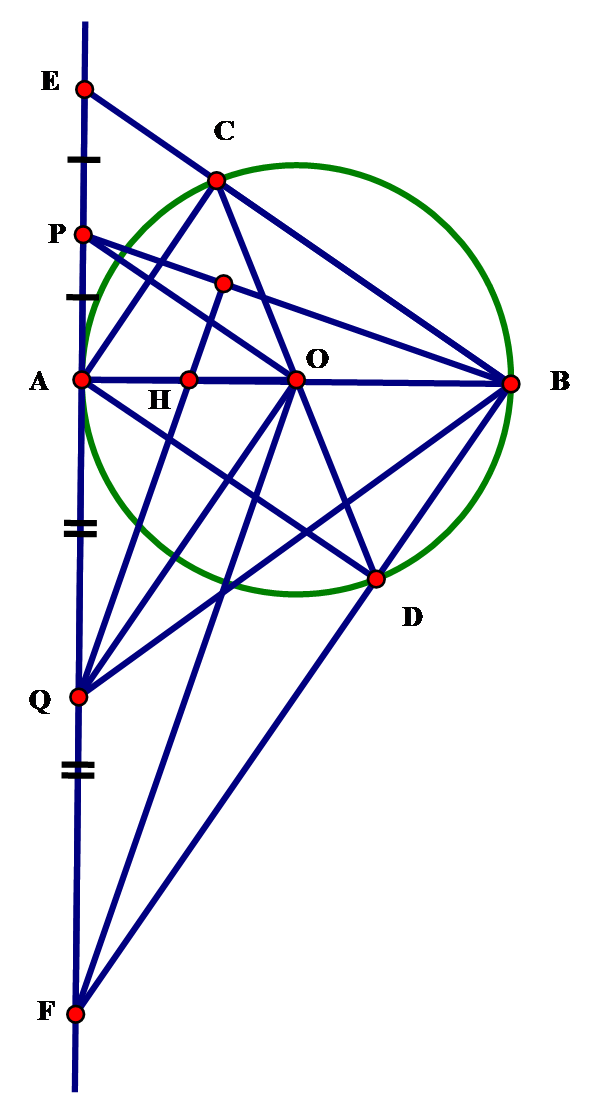
(3)
Áp dụng bất đẳng thức Cô si với hai số không âm AE và AF ta có: AE + AF (4)
( Dấu “=” xảy ra AE =AF)
Từ (3) và (4) (5)
Lại có: Áp dụng hệ thức trong tam giác vuông EBF ta có:
AE.AF = AB2 (6) Từ (5) và (6) ta có SBPQ
Xảy ra dấu bằng khi AE = AF
Tam giác EBF vuông cân tại B
ACBD là hình vuông nên CD vuông góc AB
Vậy: Khi đường kính CD vuông góc với đường kính AB thì tam giác PBQ có diện tích nhỏ nhất
Câu 39:
Trên đoạn thẳng AB cho điểm C nằm giữa A và B Trên cùng một nửa mặt phẳng có bờ là AB kẻ hai tia Ax và By cùng vuông góc với AB Trên tia Ax lấy điểm I, tia vuông góc với CI tại C cắt tia By tại K. Đường tròn đường kính IC cắt IK tại P ( P khác I)
Chứng minh tứ giác CPKB nội tiếp một đường tròn, chỉ rõ đường tròn này.
 Xem đáp án
Xem đáp án
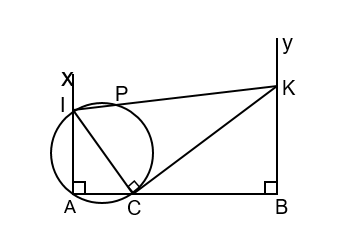
Có: (góc nội tiếp chắn nửa đường tròn);
Do nên .
Suy ra: hay tứ giác CPKB nội tiếp đường tròn đường kính CK.
Câu 40:
Trên đoạn thẳng AB cho điểm C nằm giữa A và B Trên cùng một nửa mặt phẳng có bờ là AB kẻ hai tia Ax và By cùng vuông góc với AB Trên tia Ax lấy điểm I, tia vuông góc với CI tại C cắt tia By tại K. Đường tròn đường kính IC cắt IK tại P ( P khác I)
 Xem đáp án
Xem đáp án
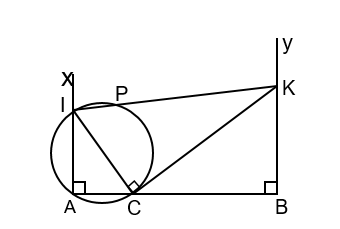
Ta có: (góc nội tiếp và góc tạo bởi tia tiếp tuyến và một dây cùng chắn một cung); (1)
Mặt khác tứ giác PCBK nội tiếp nên: (2)
Từ (1) và (2) ta có điều phải chứng minh.
Câu 41:
Trên đoạn thẳng AB cho điểm C nằm giữa A và B Trên cùng một nửa mặt phẳng có bờ là AB kẻ hai tia Ax và By cùng vuông góc với AB Trên tia Ax lấy điểm I, tia vuông góc với CI tại C cắt tia By tại K. Đường tròn đường kính IC cắt IK tại P ( P khác I)
Giả sử A, B, I cố định. Hãy xác định vị trí của điểm C sao cho diện tích tứ giác ABKI lớn nhất.
 Xem đáp án
Xem đáp án
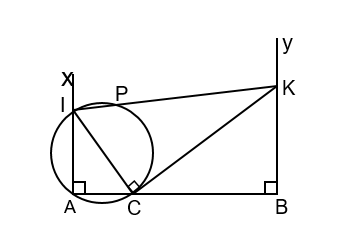
Từ giả thiết suy ra tứ giác AIKB là hình thang vuông, gọi s là diện tích của AIKB, khi đó ta có: . Dễ thấy s lớn nhất khi và chỉ khi KB lớn nhất (do A, B, I cố định).
Xét các tam giác vuông AIC và BKC có: và suy ra: (góc có cạnh tương ứng vuông góc) hay đồng dạng với (g-g).
Suy ra: , khi đó: BK lớn nhất ACBC lớn nhất
Theo BĐT Côsi có: , dấu “=” xảy ra khi và chỉ khi C là trung điểm của AB Vậy diện tích tứ giác AIBK lớn nhất khi và chỉ khi C là trung điểm của AB
Câu 42:
Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI = AO. Kẻ dây MN vuông góc với AB tại I. Gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và.B Nối AC cắt MN tại E.
Chứng minh tứ giác IECB nội tiếp được trong một đường tròn.
 Xem đáp án
Xem đáp án
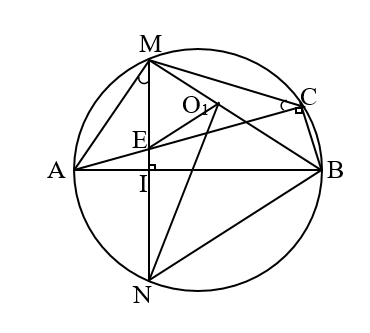
* (giả thiết)
* (góc nội tiếp chắn nửa đường tròn)
* Kết luận: Tứ giác IECB là tứ giác nội tiếp
Câu 43:
Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI = AO. Kẻ dây MN vuông góc với AB tại I. Gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và. B Nối AC cắt MN tại E.
Chứng minh ∆AME ∆ACM và = AE.AC
 Xem đáp án
Xem đáp án
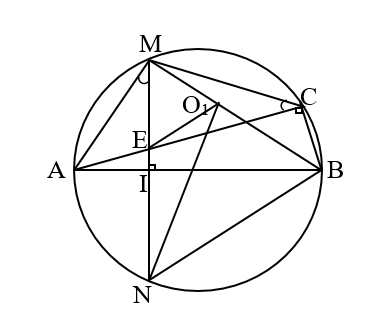
Ta có:
* sđ = sđ
*
*Góc A chung, suyra ∆AME ∆ACM.
* Do đó:
Câu 44:
Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI = AO. Kẻ dây MN vuông góc với AB tại I. Gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và. B Nối AC cắt MN tại E.
Chứng minh AE.AC - AI.IB = .
 Xem đáp án
Xem đáp án

* MI là đường cao của tam giác vuông MAB nên MI2 = AI.IB
* Trừ từng vế của hệ thức ở câu b) với hệ thức trên
* Ta có:
Câu 45:
Cho đường tròn (O), đường kính AB cố định, điểm I nằm giữa A và O sao cho AI = AO. Kẻ dây MN vuông góc với AB tại I. Gọi C là điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và.B Nối AC cắt MN tại E.
 Xem đáp án
Xem đáp án
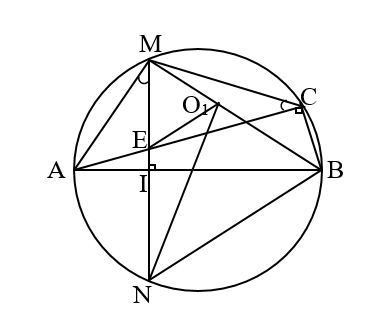
* Từ câu b) suy ra AM là tiếp tuyến của đường tròn ngoại tiếp tam giác CME. Do đó tâm O1 của đường tròn ngoại tiếp tam giác CME nằm trên BM. Ta thấy khoảng cách NO1 nhỏ nhất khi và chỉ khi NO1 BM.)
* Dựng hình chiếu vuông góc của N trên BM ta được O1. Điểm C là giao của đường tròn đã cho với đường tròn tâm O1, bán kính O1M.
Câu 46:
Cho hình bình hành ABCD có đỉnh D nằm trên đường tròn đường kính AB = 2R. Hạ BN và DM cùng vuông góc với đường chéo AC.Chứng minh tứ giác: CBMD nội tiếp được
 Xem đáp án
Xem đáp án
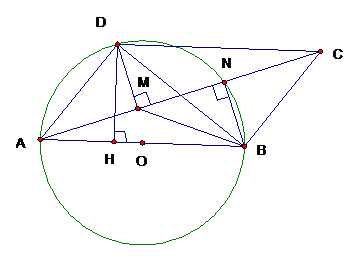
(Góc nội tiếp chắn nửa đường tròn)
mà AD//BC (gt) => DB^BC
Xét tứ giác DMBC có => Tứ giác nội tiếp.
Câu 47:
Cho hình bình hành ABCD có đỉnh D nằm trên đường tròn đường kính AB = 2R. Hạ BN và DM cùng vuông góc với đường chéo AC. Chứng minh rằng: DBDC = DN.AC
 Xem đáp án
Xem đáp án
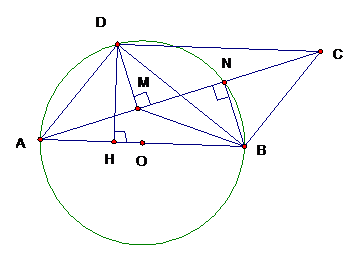 Ta có DDBN đồng dạng với DCAD
Ta có DDBN đồng dạng với DCAD
( , )
=> => a
Câu 48:
Cho hình bình hành ABCD có đỉnh D nằm trên đường tròn đường kính AB = 2R. Hạ BN và DM cùng vuông góc với đường chéo AC. Xác định vị trí của điểm D để diện tích hình bình hành ABCD có diện tích lớn nhất và tính diện tích trong trường hợp này
 Xem đáp án
Xem đáp án
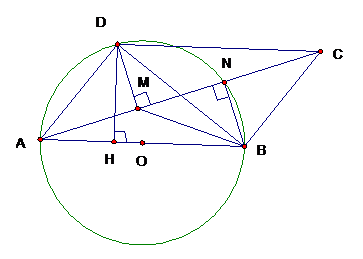
Do AB không đổi = 2R
=> max DH max D nằm chính giữa cung AB
Câu 49:
Cho đường tròn (O), dây AB không đi qua tâm. Trên cung nhỏ AB lấy điểm M (M không trùng với A, B). Kẻ dây MN vuông góc với AB tại H. Kẻ MK vuông góc với AN .
 Xem đáp án
Xem đáp án
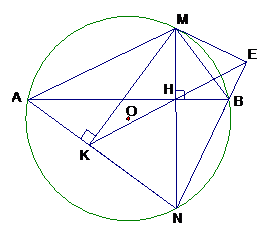
Từ giả thiết: ,
Bốn điểm A, K, H, M cùng thuộc một đường tròn
Câu 50:
Cho đường tròn (O), dây AB không đi qua tâm. Trên cung nhỏ AB lấy điểm M (M không trùng với A, B). Kẻ dây MN vuông góc với AB tại H. Kẻ MK vuông góc với AN .
 Xem đáp án
Xem đáp án
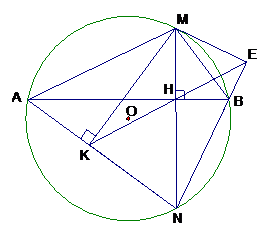
= sđ (1)
= sđ (2)
Từ (1) và (2)
MN là phân giác của góc KMB
Câu 51:
Cho đường tròn (O), dây AB không đi qua tâm. Trên cung nhỏ AB lấy điểm M (M không trùng với A, B). Kẻ dây MN vuông góc với AB tại H. Kẻ MK vuông góc với AN .
Khi M di chuyển trên cung nhỏ AB Gọi E là giao điểm của HK và BN.
Xác định vị trí của điểm M để (MK.AN + ME.NB) có giá trị lớn nhất.
 Xem đáp án
Xem đáp án
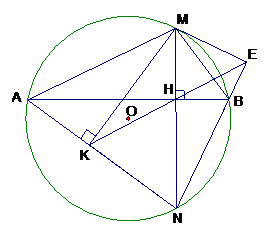
sđ ; sđ
cùng thuộc một đường tròn
lớn nhất MN.AB lớn nhất
MN lớn nhất (Vì AB= const ) M là chính giữa
Câu 52:
Cho (O),dây cung AB. Từ điểm M bất kỳ trên cung AB sao cho MA> MB (M¹A và M¹B), kẻ dây cung MN vuông góc với AB tại H. Gọi MQ là đường cao của tam giác MAN.
C/m 4 điểm A;M;H;Q cùng nằm trên một đường tròn.
 Xem đáp án
Xem đáp án
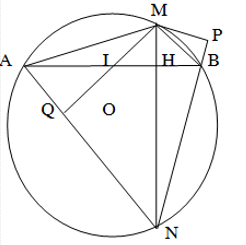
C/m:A,Q,H,M cùng nằm trên một đường tròn.
Câu 53:
Cho (O),dây cung AB. Từ điểm M bất kỳ trên cung AB sao cho MA> MB (M¹A và M¹B), kẻ dây cung MN vuông góc với AB tại H. Gọi MQ là đường cao của tam giác MAN.
 Xem đáp án
Xem đáp án
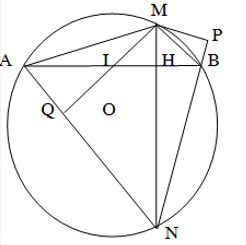
C/m: NQ.NA=NH.NM.
Xét hai Dvuông NQM và DNAH đồng dạng. (g-g)
Câu 54:
Cho (O),dây cung AB. Từ điểm M bất kỳ trên cung AB sao cho MA> MB (M¹A và M¹B), kẻ dây cung MN vuông góc với AB tại H. Gọi MQ là đường cao của tam giác MAN.
 Xem đáp án
Xem đáp án
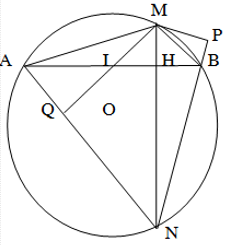
C/m MN là phân giác của góc BMQ. Có hai cách:
(Cùng phụ với góc ANH)
(Cùng chắn cung NB) Þ đpcm
Câu 55:
Cho (O),dây cung AB. Từ điểm M bất kỳ trên cung AB sao cho MA> MB (M¹A và M¹B), kẻ dây cung MN vuông góc với AB tại H. Gọi MQ là đường cao của tam giác MAN.
Hạ đoạn thẳng MP vuông góc với BN;xác định vị trí của M trên cung AB để MQ.AN+MP.BN có giác trị lớn nhất.
 Xem đáp án
Xem đáp án
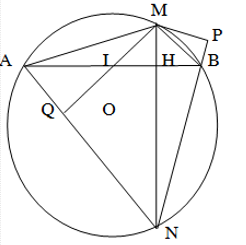
Xác định vị trí của M trên cung AB để MQ.AN+MP.BN có giác trị lớn nhất.
Ta có
2SDMAN + 2SDMBN = MQ.AN+MP.BN
Ta lại có: 2SDMAN + 2SDMBN =2(SDMAN + SDMBN)=2SAMBN=2. =AB.MN
Vậy: MQ.AN+MP.BN=AB.MN
Mà AB không đổi nên tích ABMN lớn nhất Û MN lớn nhấtÛMN là đường kính
ÛM là điểm chính giữa cung AB
Câu 56:
Cho đường tròn (O) đường kính AB Gọi I là trung điểm của OA Vẽ đường tron tâm I đi qua A, trên (I) lấy P bất kì, AP cắt (O) tại Q. Chứng minh rằng các đường tròn (I) và (O) tiếp xúc nhau tại A
 Xem đáp án
Xem đáp án
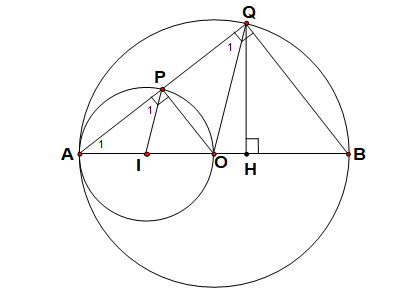
Ta có OI = OA – IA mà OA và IA lần lượt là các bán kính của đường tròn (O) và đường tròn (I). Vậy đường tròn (O) và đường tròn (I) tiếp xúc nhau tại A
Câu 57:
Cho đường tròn (O) đường kính AB Gọi I là trung điểm của OA Vẽ đường tron tâm I đi qua A, trên (I) lấy P bất kì, AP cắt (O) tại Q. Chứng minh IP // OQ.
 Xem đáp án
Xem đáp án
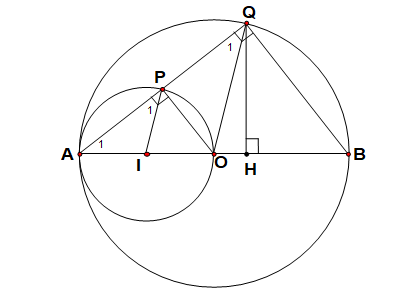
DOAQ cân tại O ( vì OA và OQ cùng là bán kính ) => ÐA1 = ÐQ1
DIAP cân tại I ( vì IA và IP cùng là bán kính ) => ÐA1 = ÐP1
=> ÐP1 = ÐQ1 mà đây là hai góc đồng vị nên suy ra IP // OQCâu 58:
Cho đường tròn (O) đường kính AB Gọi I là trung điểm của OA Vẽ đường tron tâm I đi qua A, trên (I) lấy P bất kì, AP cắt (O) tại Q. Chứng minh rằng AP = PQ.
 Xem đáp án
Xem đáp án
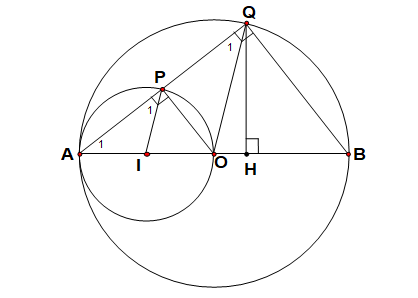
ÐAPO = 900 (nội tiếp chắn nửa đường tròn ) => OP ^ AQ => OP là đường cao của DOAQ mà DOAQ cân tại O nên OP là đường trung tuyến => AP = PQ.
Câu 59:
Cho đường tròn (O) đường kính AB Gọi I là trung điểm của OA Vẽ đường tron tâm I đi qua A, trên (I) lấy P bất kì, AP cắt (O) tại Q. Xác định vị trí của P để tam giác AQB có diện tích lớn nhất.
 Xem đáp án
Xem đáp án
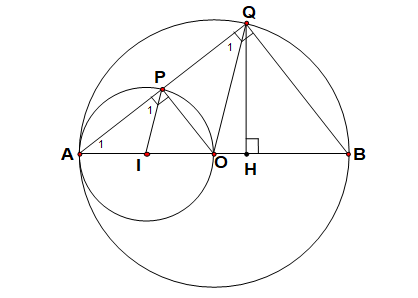
(HD) Kẻ QH ^ AB ta có SAQB = ABQH. mà AB là đường kính không đổi nên SAQB lớn nhất khi QH lớn nhất. QH lớn nhất khi Q trùng với trung điểm của cung AB Để Q trùng với trung điểm của cung AB thì P phải là trung điểm của cung AO.
Thật vậy P là trung điểm của cung AO => PI ^ AO mà theo trên PI // QO => QO ^ AB tại O => Q là trung điểm của cung AB và khi đó H trung với O; OQ lớn nhất nên QH lớn nhất.
