Dạng 6. Sử dụng tỉ số lượng giác.
-
2883 lượt thi
-
2 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Chứng minh rằng trong các tam giác cân có cùng diện tích tam giác có cạnh đáy nhỏ hơnlà tam giác có góc ở đỉnh nhỏ hơn.
 Xem đáp án
Xem đáp án
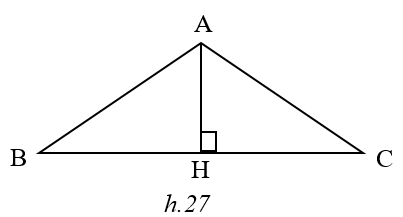
Xét các tam giác ABC cân tại A có cùng diện tích S. Kẻ đường cao AH . Đặt = a
Tam giác AHC vuông tại H, ta có :
AH = HC .cotg = BC.cotg
Do đó : S = BC.AH = BC. BC.cotg = BC2cotg
BC =
Do S không đổi nên :
BC nhỏ nhất tg nhỏ nhất nhỏ nhất a nhỏ nhất nhỏ nhất
Câu 2:
Cho hình chữ nhật ABCD. Trên các cạnh BC,CD lần lượt lấy các điểm K,M sao cho BK : KC = 4 : 1, CM : MD = 4 : 1.Tìm tỉ số AB : BC để số đo góc lớn nhất .
( Cho công thức biến đổi tan( x +y )= )
 Xem đáp án
Xem đáp án
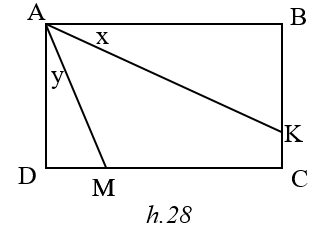
lớn nhất nhỏ nhất
x + y nhỏ nhất tan (x + y) nhỏ nhất
Giả sử AB : BC = 1 : m ( m> 0)
tan x =
tan y =
tan( x +y )=
tan (x + y) nhỏ nhất nhỏ nhất
Theo bất đẳng thức Cô-si ta có:
≥
Dấu đẳng thức xảy ra m =
Vậy x + y nhỏ nhất khi và chỉ khi m =
Do đó lớn nhất khi và chỉ khi AB : BC = 2 : 1a
