19 câu hỏi trắc nghiệm thuộc Dạng 8. Bài luyện tập tổng hợp có đáp án

Câu 1:

Cho hình vuông ABCD . Hãy xác định đường thẳng d đi qua tâm hình vuông sao cho tổng các khoảng cách từ bốn đỉnh của hình vuông đến đường thẳng đó là : Lớn nhất

Xem đáp án

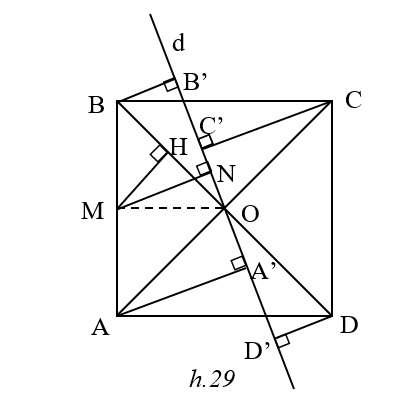
Xét trường hợp d cắt hai cạnh đối BC và AD (h.29)

Gọi m là tổng các khoảng cách từ bốn đỉnh hình vuông đến D.

m =2(AA’ +BB’)

Gọi M, N lần lượt là trung điểm của AB và A’B’

Suy ra : m = 4MN do đó:

m lớn nhất Û MN lớn nhất

m nhỏ nhất Û MN nhỏ nhất

MN £ MO Þ m lớn nhất Û M≡O Û d//AB

Câu 2:

Cho hình vuông ABCD . Hãy xác định đường thẳng d đi qua tâm hình vuông sao cho tổng các khoảng cách từ bốn đỉnh của hình vuông đến đường thẳng đó là :Nhỏ nhất

Xem đáp án

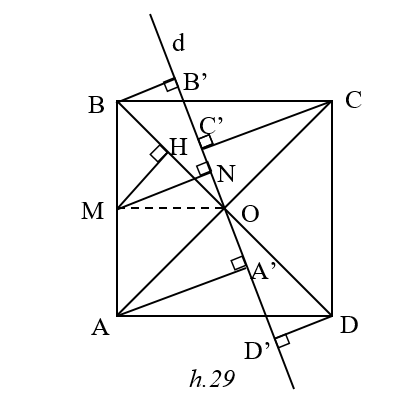
Xét trường hợp d cắt hai cạnh đối BC và AD (h.29)

Gọi m là tổng các khoảng cách từ bốn đỉnh hình vuông đến D.

m =2(AA’ +BB’)

Gọi M, N lần lượt là trung điểm của AB và A’B’

Suy ra : m = 4MN do đó:

m lớn nhất Û MN lớn nhất

m nhỏ nhất Û MN nhỏ nhất

kẻ MH ^ OB . Chứng minh MN ≥MH Þ MN nhỏ nhất Û N ≡H Û d≡BD hoặc d ≡AC.

Câu 3:

Cho DABC vuông cân tại A các điểm D,E theo thứ tự di chuyển trên các cạnh AB , AC sao cho BD = AE . Xác định vị trí các điểm D,E sao cho :DE có độ dài nhỏ nhất .

Xem đáp án

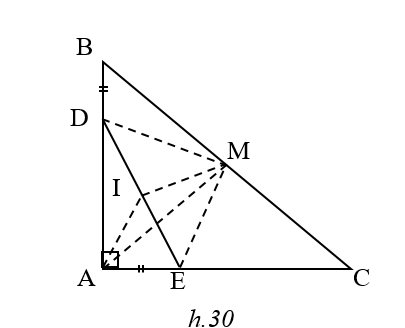Gọi M là trung điểm của BC .

DBDM = DAEM Þ $\hat{B M D} = \hat{A M E}$

Þ $\hat{D M E} = \hat{D M A} + \hat{A M E} = \hat{D M A} + \hat{B M D} = \hat{B M A} = 90^{0}$

Gọi I là trung điểm của DE .

DE = DI+IE =AI + IM ≥ AM

Min DE = AM Û I là trung điểm của AM

Û D là trung điểm của AB và E là trung điểm của AC

Câu 4:

Cho DABC vuông cân tại A các điểm D,E theo thứ tự di chuyển trên các cạnh AB , AC sao cho BD = AE . Xác định vị trí các điểm D,E sao cho :Tứ giác BDEC có diện tích lớn nhất

Xem đáp án

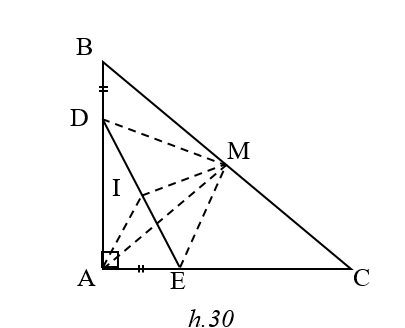
Đặt AE = x, AB =AC =a thì AD = a - x , S_ADE =

S_BDEC nhỏ nhất Û S_ADElớn nhất Û x(a - x) lớn nhất

Do x +( a- x) = a không đổi nên x( a - x) lớn nhất Û x = a - x Û x = a/2

Khi đó D là trung điểm của AB và E là trung điểm của AC

Câu 5:

Cho D ABC vuông tại A có BC = a , diện tích là S . Gọi m là trung điểm của BC . Hai dường thẳng thay đổi qua M và vuông góc với nhau cắt các cạnh AB , AC ở D ,E .Tìm :Giá trị nhỏ nhất của đoạn thẳng DE .

Xem đáp án

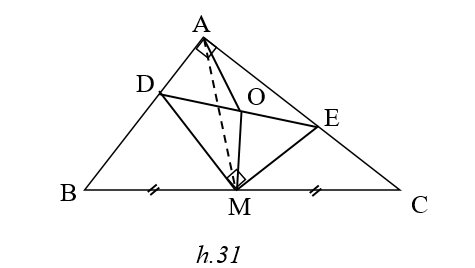
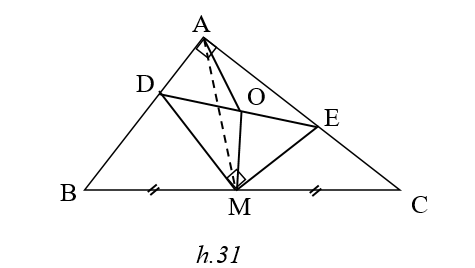
(h.31)Gọi O là trung điểm của DE

Ta có OA = OD =OE = OM

Þ DE = OA + OM ≥ AM =

minDE = a/2 Û O là trung điểm của AM

Û D là trung điểm của AB và E là trung điểm của AC

Câu 6:

Cho D ABC vuông tại A có BC = a , diện tích là S . Gọi m là trung điểm của BC . Hai dường thẳng thay đổi qua M và vuông góc với nhau cắt các cạnh AB , AC ở D ,E .Tìm : Giá trị nhỏ nhất của diện tích D MDE

Xem đáp án

(h.32)Kẻ MH ^ AB , MK ^ AC

ME ≥ MK , MD ≥ MH .

2S_MDE = MD.ME ≥ MH.MK = $\frac{A C}{2}$ . $\frac{A C}{2}$ = $\frac{S}{2}$

minS_MDE = Û D ≡ H và E ≡ K

Câu 7:

Cho điểm m di chuyển trên đoạn thẳng AB .Vẽ các tam giác đềuAMC và BMD về một phía của AB . Xác định vị trí của M để tổng diện tích hai tam giác đều tren là nhỏ nhất .

Xem đáp án

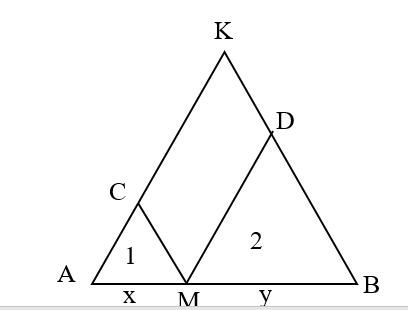
Gọi K là giao điểm của AC và BD .

Các tam giác AMC ,BMD đồng dạng với DAKB

Đặt AM = x ,BM = y , AB = a ta có :

$\frac{S_{1}}{S} = {(\frac{x}{a})}^{2}$ ; $\frac{S_{2}}{S} = {(\frac{y}{a})}^{2}$

Þ $\frac{S_{1} + S_{2}}{S} = \frac{x^{2} + y^{2}}{a^{2}} \geq \frac{{(x + y)}^{2}}{2 a^{2}} = \frac{a^{2}}{2 a^{2}} = \frac{1}{2}$

Dấu đẳng thức xảy ra khi và chỉ khi x = y

Do đó : min (S₁ +S₂) = $\frac{1}{2}$ Û M là trung điểm của AB.

Câu 8:

Cho tam giác nhọn ABC có các cạnh a,b,c tương ứng đường cao AH =H. Hãy dựng hình chữ nhật MNPQ nội tiếp trong tam giác ABC sao cho nó có diện tích lớn nhất . Biết M ÎAB ; N Î AC ; P,Q Î BC.

Xem đáp án

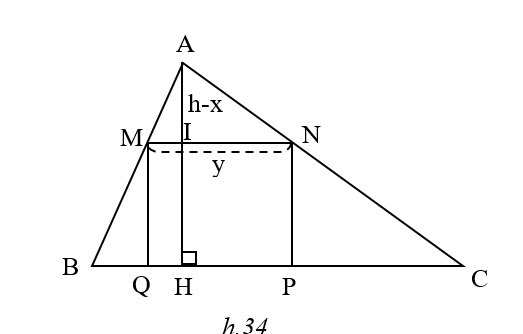
Gọi I là giao điểm của AH và MN

Đặt NP =x ; MN = y ; AI = h - x

DAMN $~$ D ABC

Þ $\frac{M N}{B C} = \frac{A I}{A H} \Rightarrow \frac{y}{a} = \frac{h - x}{h} \Rightarrow y = a . \frac{h - x}{h}$

Þ S_MNPQ = xy = . x(h - x)

Þ S_MNPQ lớn nhất Û x(h - x)lớn nhất

x +(h - x) = h không đổi nên

x(h - x) lớn nhất Û x = h - x Û x = h/2

Khi đó MN là đường trung bình của DABC

Câu 9:

Cho D ABC vuông tại A . Từ một điểm I nằm trong tam giác ta kẻ IM ^ BC, IN ^ AC , IK ^AB . Tìm vị trí của I sao cho tổng IM² +IN² +IK² nhỏ nhất.

Xem đáp án

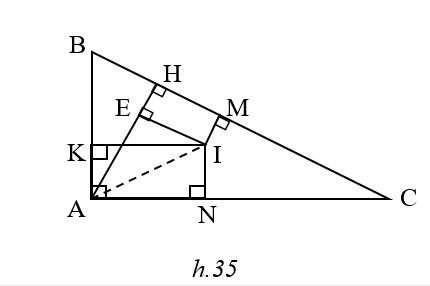
Kẻ AH ^BC , IE ^AH

ANIK ,IMHE là các hình chữ nhật.

IK²+ IN² = IK² +AK² = AI² ≥ AE²

IM = EH

nên IK²+ IN² + IM² = AI²+EH² ≥ AE²+EH²

Đặt AE = x , EH =y ta có :

Þ IK²+ IN² + IM² ≥ .

Dấu “=” xảy ra khi I là trung điểm của đường cao AH.

Câu 10:

Cho tam giác nhọn ABC .Từ một điểm I nằm trong tam giác ta kẻ IM ^ BC, IN ^ AC , IK ^AB . Đặt AK =x ; BM = y ; CN = z.Tìm vị trí của I sao cho tổng x² +y² +z²nhỏ nhất.

Xem đáp án

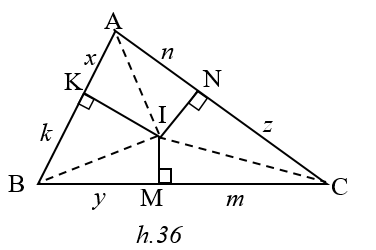
Đặt BK = k , CM = m , AN = n ,

BC = a , AC = b , AB = c .

x² +y² +z² =

=(IA² - IK² ) + (IB² - IM² ) + (IC² - IN² )

= (IA² - IN² ) + (IB² - IK² ) + (IC² - IM² ) = n² + k² + m²

Þ 2(x² +y² +z² ) = x² +y² +z² + n² + k² + m²

= ( x²+ k² )+( y²+ m² )+( z²+ n² )

x²+ k² ≥ $\frac{{(x + k)}^{2}}{2} = \frac{A B^{2}}{2} = \frac{c^{2}}{2}$ y²+ m² ≥ $\frac{{(y + m)}^{2}}{2} = \frac{B C^{2}}{2} = \frac{a^{2}}{2}$

z²+ n² ≥ $\frac{{(z + n)}^{2}}{2} = \frac{A C^{2}}{2} = \frac{b^{2}}{2}$

Þ x² +y² +z² ≥ $\frac{a^{2} + b^{2} + c^{2}}{4}$ .

min(x² +y² +z² ) = $\frac{a^{2} + b^{2} + c^{2}}{4}$ Û x = k , y = m , z = n.

Û I là giao điểm của các đường trung trực của DABC.

Câu 11:

Cho nửa đường tròn có đường kính AB = 10 cm .Một dây CD có độ dài 6cm có hai đầu di chuyển trên nửa đường tròn . Gọi E và F theo thứ tự là hình chiếu của A và B trên CD. Tính diện tích lớn nhất của tứ giác ABFE.

Xem đáp án

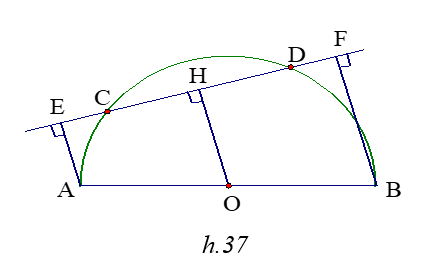
Kẻ OH ^CD , ta tính được OH = 4cm

S_ABFE = 1/2(AE + BF).EF

= OH.EF £ OH. AB = 4.10 =40

max S_ABEF =40 cm²

Û EF // AB , khi đó OH ^ AB

Câu 12:

Cho hình vuông ABCD cạnh a .Vẽ cung BD tâm A bán kính a (nằm trong hình vuông ) .một tiếp tuyến bất kỳ với cung đó cắt BC, CD theo thứ tự ở M và N. Tính độ dài nhỏ nhất của MN.

Xem đáp án

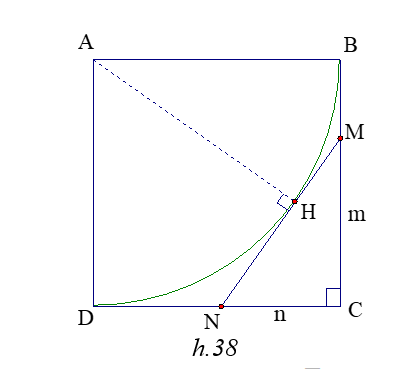
Đặt CM = m , CN = n , MN = x

m + n + x = 2CD = 2a và m² +n² = x²

Do đó : x²= m² +n² ≥

$\Rightarrow$ 2x² ≥ ( 2a - x)² Þ ≥ 2a - x

$\Rightarrow$ x ≥

$\Rightarrow$ min MN =2a Û m = n . Khi đó tiếp tuyến MN // BD , AM là tia phân giác của

$\Rightarrow$ AN là phân giác của

Câu 13:

Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A .Qua A vẽ hai tia vuông góc với nhau , chúng cắt các đường tròn (O) , (O’) lần lượt tại B và C. Xác định vị trí của các tia đó để D ABC có diện tích lớn nhất .

Xem đáp án

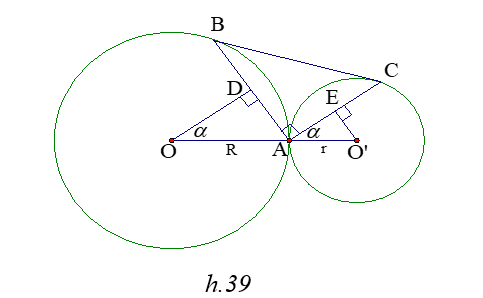
Kẻ OD ^ AB ; O’E ^ AC ta có:

S_ABC = AB.AC = .2AD.2AE= 2.AD.AE

Đặt OA =R ; O’A = r ;

AD = R sina ; AE = r cosa

Þ S_ABC = Rr. 2sina .cosa

2sina .cosa £ sin²a + cos²a =1

Þ S_ABC £ Rr

Þ Do đó :

max S_ABC = Rr Û sina = cosa Û sina = sin( 90⁰- a ) Û a = 90⁰ - a Û a = 45⁰.

Vậy nếu ta vẽ các tia AB,AC lần lượt tạo với các tia AO, AO’ thành các góc thì D ABC có diện tích lớn nhất .

Câu 14:

Cho đường tròn (O;R) đường kính BC , A là một điểm di động trên đường tròn . Vẽ tam giác đều ABM có A và M nằm cùng phía đối với BC . Gọi H là chân đường vuông góc kẻ từ C xuống MB. Gọi D, E , F, G theo thứ tự là trung điểm của OC, CM, MH, OH . Xác định vị trí của điểm A để diện tích tứ giác DEFG đạt giá trị lớn nhất.

Xem đáp án

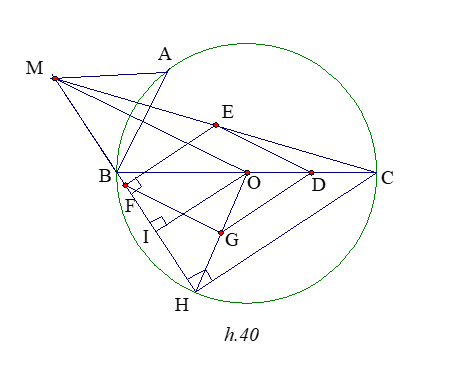
DEFG là hình bình hành.

Kẻ OI ^FH , ta có OI là đường trung bình của D BHC nên

OI = ½ HC = GD

MO là đường trung trực của AB nên Þ OI = ½

OM Þ GD = ½ OM

Mà ED = ½ OM Þ EG = GD

Þ DEFG là hình thoi

Þ ÞDEFG đều

Þ S_DEFG =2S_EFG = 2. $\frac{{EF}^{2} \sqrt{3}}{4} = \frac{{EF}^{2} \sqrt{3}}{2}$ = $\frac{{(\frac{H C}{2})}^{2} \sqrt{3}}{2}$ £ $\frac{{(\frac{B C}{2})}^{2} \sqrt{3}}{2}$ = $\frac{R^{2} \sqrt{3}}{2}$

max S = $\frac{R^{2} \sqrt{3}}{2}$ Û H ≡ B Û $\hat{M B C} = 90^{0}$ Û $\hat{A B C} = 30^{0}$ Û AC = R.

Câu 15:

Cho DABC nội tiếp đường tròn (O) D là điểm bất kỳ thuộc cung BC không chứa A và không trùng với B,C. Gọi H,I,K theo thứ tự là chân các đường vuông góc kẻ từ D đến các đường thẳng BC , AC, AB . Đặt BC = a , AC = b ,AB = c, DH = x , DI = y , DK = z . Chứng minh rằng : $\frac{b}{y} + \frac{c}{z} = \frac{a}{x}$

Xem đáp án

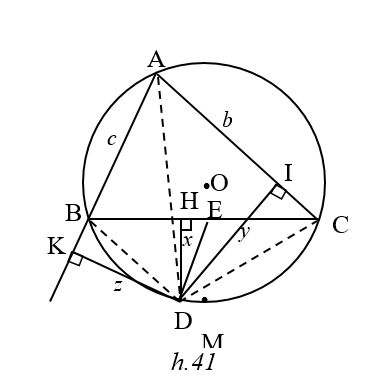
Lấy E trên BC sao cho

DCDE đồng dạng với D ADB

Þ $\frac{D H}{D K} = \frac{C E}{A B} \Rightarrow \frac{x}{z} = \frac{C E}{c} \Rightarrow \frac{c}{z} = \frac{C E}{x}$

Tương tự DBDE đồng dạng với D ADC

Þ $\frac{D H}{D I} = \frac{B E}{A C} \Rightarrow \frac{x}{y} = \frac{B E}{b} \Rightarrow \frac{b}{y} = \frac{B E}{x}$

Þ $\frac{b}{y} + \frac{c}{z} = \frac{B E + C E}{x} = \frac{a}{x}$

Câu 16:

Cho DABC nội tiếp đường tròn (O) D là điểm bất kỳ thuộc cung BC không chứa A và không trùng với B,C. Gọi H,I,K theo thứ tự là chân các đường vuông góc kẻ từ D đến các đường thẳng BC , AC, AB . Đặt BC = a , AC = b ,AB = c, DH = x , DI = y , DK = z .Tìm vị trí của điểm D để tổng $\frac{a}{x} + \frac{b}{y} + \frac{c}{z}$ nhỏ nhất

Xem đáp án

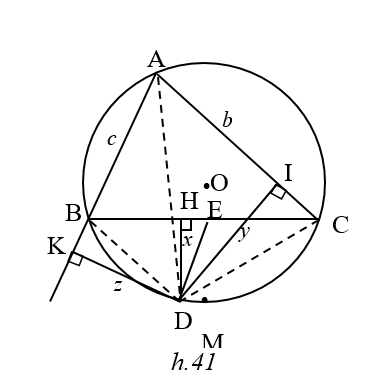
$\frac{a}{x} + \frac{b}{y} + \frac{c}{z}$ = $\frac{a}{x} + \frac{a}{x}$ = $\frac{2 a}{x}$ .Do đó S nhỏ nhất Û $\frac{a}{x}$ nhỏ nhất Û x lớn nhất Û D≡M ( M là điểm chính giữa của cung BC không chứa A)

Câu 17:

Cho DABC nhọn , điểm M di chuyển trên cạnh BC .Gọi P ,Q là hình chiếu của M trên AB , AC . Xác định vị trí của điểm M để PQ có độ dài nhỏ nhất.

Xem đáp án

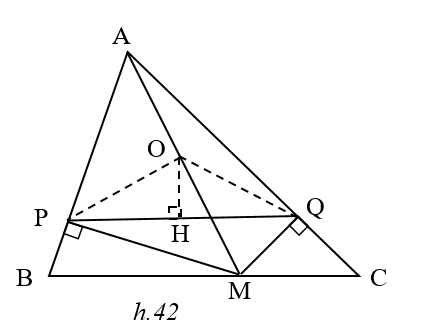
Tứ giác APMQ là tứ giác nội tiếp . Gọi O là tâm đường tròn ngoại tiếp tứ giác APMQ.

Kẻ OH ^ PQ . Đặt =a thì = a

PQ = 2 PH = 2.OP sina = AM sina

Do a không dổi nên

PQ nhỏ nhất Û AM nhỏ nhất Û AM ^BC.

Câu 18:

Cho đoạn thẳng AB và một điểm C trên AB .Vẽ trên cùng một nửa mặt phẳng bờ AB các nửa đường tròn có đường kính AB,AC,BC . Xác định vị trí của điểm C trên đoạn AB để diện tích phần giới hạn bởi ba nửa đường tròn đó dạt giá trị lớn nhất.

Xem đáp án

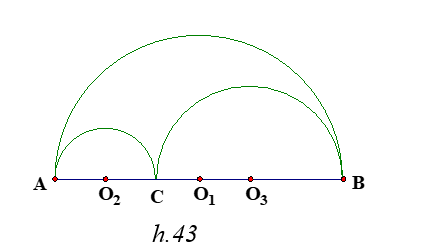
Gọi (O_1;r₁);(O_2;r₂);(O_3;r₃) là các đường tròn có đường kính là Ab,AC,BC

Đặt AB = 2a , AC =2x thì r₁ = a , r₂= x Suy ra BC =2a - 2x và r₃ = a - x

Gọi S là diện tích giới hạn bởi ba đường tròn

Ta có : $S = \frac{π r_{1}^{2}}{2} - (\frac{π r_{2}^{2}}{2} + \frac{π r_{3}^{2}}{2})$ $\frac{π a^{2}}{2} - \frac{π x^{2}}{2} - \frac{π {(a - x)}^{2}}{2} = π x (a - x)$

S lớn nhất Û x( a -x) lớn nhất

Mặt khác x + (a - x) = a không đổi nên

x( a -x) lớn nhất Û x = a - x Û x = $\frac{a}{2}$ Û C ≡O₁

Lúc đó ta có S = $\frac{π a^{2}}{4}$

Câu 19:

Cho đường tròn (O;R) . Trong đường tròn (O) vẽ hai đường tròn (O₁) và (O₂) tiếp xúc ngoài nhau và tiếp xúc trong với (O) trong đó bán kính đường tròn (O₂) gấp đôi bán kính đường tròn (O₁). Tìm giá trị nhỏ nhất của diện tích phần hình tròn (O) nằm ngoài các hình tròn (O₁) và(O₂)

Xem đáp án

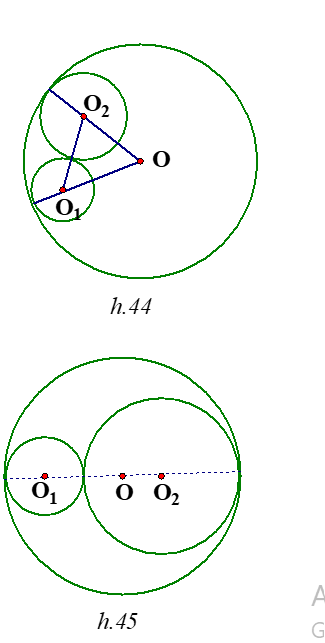
Gọi x là bán kính đường tròn (O₁) Khi đó 2x là bán kính đường tròn (O₂) (h.44)

Xét DOO₁O₂ ta có : O₁O₂ £ O O₁ +OO₂

Þ 3x £ (R - x) +( R - 2x) Þ 6x £ 2R Þ x £ $\frac{R}{3}$

Gọi S là phần diện tích hình tròn (O) nằm ngoài các đường tròn (O₁)và (O₂) , ta có :

S = $π R^{2} - π x^{2} - π 4 x^{2} = π (R^{2} - 5 x^{2})$

Do x £ $\frac{R}{3}$ nên x² £ $\frac{R^{2}}{9}$ Þ S ≥ $\frac{4 π R^{2}}{9}$ ;

min S = $\frac{4 π R^{2}}{9}$ Û x = $\frac{R}{3}$

Khi đó O₁,O,O₂ thẳng hàng và bán kính các đường tròn (O₁) và (O₂) là $\frac{R}{3}$ và $\frac{2 R}{3}$ (h.45).

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập Toán 9 Chủ đề 7: Cực trị hình học có đáp án

Dạng 8. Bài luyện tập tổng hợp có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương