5 câu hỏi trắc nghiệm thuộc Đề thi Giữa kì 1 Toán lớp 9 có đáp án (Đề 2)

Câu 1:

1. Thực hiện phép tính.

a. $\sqrt{81} - \sqrt{80} . \sqrt{0, 2}$

b. $\sqrt{{(2 - \sqrt{5})}^{2}} - \frac{1}{2} \sqrt{20}$

2. Tìm điều kiện của để các biểu thức sau có nghĩa:

a. $\sqrt{- x + 1}$

b. $\sqrt{\frac{1}{x^{2} - 2 x + 1}}$

Xem đáp án

1.

a. $\sqrt{81} - \sqrt{80} . \sqrt{0, 2} = \sqrt{9^{2}} - \sqrt{80 .0, 2}$ $= 9 - \sqrt{16} = 9 - 4 = 5$

b. $\sqrt{{(2 - \sqrt{5})}^{2}} - \frac{1}{2} \sqrt{20} = |2 - \sqrt{5}| - \frac{1}{2} . 2 \sqrt{5}$

$= \sqrt{5} - 2 - \sqrt{5} = - 2$

2.

a. Biểu thức $\sqrt{- x + 1}$ có nghĩa $\Leftrightarrow - x + 1 \geq 0$ $\Leftrightarrow x \leq 1$

b. Biểu thức $\sqrt{\frac{1}{x^{2} - 2 x + 1}}$ có nghĩa $\Leftrightarrow \frac{1}{x^{2} - 2 x + 1} \geq 0 \Leftrightarrow x^{2} - 2 x + 1 > 0$ $\Leftrightarrow {(x - 1)}^{2} > 0 \Leftrightarrow x \neq 1$

Câu 2:

1. Phân tích đa thức thành nhân tử.

a. $ab + b \sqrt{a} + \sqrt{a} + 1$ (với $a \geq 0$ )

b. $4 a + 1$ (với $a < 0$ )

2. Giải phương trình $\sqrt{9 x + 9} + \sqrt{x + 1} = 20$

Xem đáp án

1.

a. Với $a \geq 0$ ta có: $ab + b \sqrt{a} + \sqrt{a} + 1 = b \sqrt{a} (\sqrt{a} + 1) + (\sqrt{a} + 1)$ $= (\sqrt{a} + 1) (b \sqrt{a} + 1)$

b. Với $a < 0 \Rightarrow - a > 0$

ta có: $4 a = - 4 . (- a) = - {(2 \sqrt{- a})}^{2} \Rightarrow 1 + 4 a = 1^{2} - {(2 \sqrt{- a})}^{2}$

$= (1 - 2 \sqrt{- a}) (1 + 2 \sqrt{- a})$

2. ĐK: $x \geq - 1$

$\sqrt{9 x + 9} + \sqrt{x + 1} = 20 \Leftrightarrow \sqrt{9 (x + 1)} + \sqrt{x + 1} = 20 \Leftrightarrow 3 \sqrt{x + 1} + \sqrt{x + 1} = 20$

$\Leftrightarrow 4 \sqrt{x + 1} = 20 \Leftrightarrow \sqrt{x + 1} = 5$

$\Leftrightarrow x + 1 = 25 \Leftrightarrow x = 24$ (T/m ĐKXD)

Vậy phương trình có nghiệm duy nhất:

x = 24.

Câu 3:

Cho biểu thức $A = (\frac{1}{x + 2 \sqrt{x}} - \frac{1}{\sqrt{x} + 2}) : \frac{1 - \sqrt{x}}{x + 4 \sqrt{x} + 4}$

a. Rút gọn biểu thức A.

b. Tìm x để $A = \frac{5}{3}$

Xem đáp án

Với $x > 0, x \neq 1$ ta có $A = [\frac{1}{\sqrt{x} (\sqrt{x} + 2)} - \frac{1}{\sqrt{x} + 2}] : \frac{1 - \sqrt{x}}{{(\sqrt{x} + 2)}^{2}}$

$= [\frac{1}{\sqrt{x} (\sqrt{x} + 2)} - \frac{\sqrt{x}}{\sqrt{x} (\sqrt{x} + 2)}] . \frac{{(\sqrt{x} + 2)}^{2}}{1 - \sqrt{x}}$

$= \frac{1 - \sqrt{x}}{\sqrt{x} (\sqrt{x} + 2)} . \frac{{(\sqrt{x} + 2)}^{2}}{1 - \sqrt{x}}$

$= \frac{\sqrt{x} + 2}{\sqrt{x}}$

Vậy $A= \frac{\sqrt{x} + 2}{\sqrt{x}}$ (với $x > 0; x \neq 1$ )

b. $A = \frac{5}{3} \Leftrightarrow \frac{\sqrt{x} + 2}{\sqrt{x}} = \frac{5}{3}$ (ĐK: $x > 0; x \neq 1$ )

$\Leftrightarrow 3 (\sqrt{x} + 2) = 5 \sqrt{x}$

$\Leftrightarrow 2 \sqrt{x} = 6 \Leftrightarrow \sqrt{x} = 3 \Leftrightarrow x = 9$ (TMDK)

Vậy với x = 9 thì $A = \frac{5}{3}$

Câu 4:

Cho tam giác ABC vuông tại A, đường cao AH. Biết $BC = 8cm,$ $BH = 2cm.$

a) Tính độ dài các đoạn thẳng AB, AC, AH.

b) Trên cạnh AC lấy điểm K tùy ý $(K \neq A, K \neq C)$ gọi D là hình chiếu của A trên BK. Chứng minh rằng: $BD.BK = BH.BC.$

c) Chứng minh rằng: $S_{BHD} = \frac{1}{4} S_{BKC} . \cos^{2} \hat{ABD}$

Xem đáp án

a.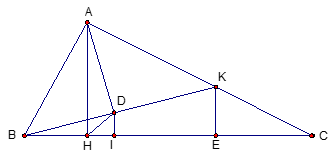

+ $ΔABC$ vuông tại A, đường cao $AH \Rightarrow {AB}^{2} = BH . BC = 2 .8 = 16$ $\Rightarrow AB = 4 cm (Vì AB > 0)$

+ ${BC}^{2} = {AB}^{2} + {AC}^{2}$ (Định lý Pitago trong tam giá vuông ABC)

$\Rightarrow AC = \sqrt{{BC}^{2} - {AB}^{2}} = \sqrt{8^{2} - 4^{2}} = \sqrt{48} = 4 \sqrt{3} cm$

+ Có $HB + HC = BC \Rightarrow HC = BC – HB = 8 – 2 = 6 cm$

${AH}^{2} = BH . CH = 2 .6 = 12$

$\Rightarrow AH = \sqrt{12} = 2 \sqrt{3} cm$ (Vì AH > 0)

b.

+ $ΔABK$ vuông tại A có đường cao AD $\Rightarrow {AB}^{2} = BD . BK$ (1)

+ Mà ${AB}^{2} = BH . BC$ (Chứng minh câu a) (2)

Từ (1) và (2) $⇒BD.BK = BH.BC$

c. Kẻ $DI ⊥ BC, KE ⊥ BC (I, K \in BC)$

$\Rightarrow \frac{S_{BHD}}{S_{BKC}} = \frac{\frac{1}{2} BH . DI}{\frac{1}{2} BC . KE} = \frac{2 . DI}{8 . KE} = \frac{1}{4} . \frac{DI}{KE}$ (3)

+ $ΔBDI ~ ΔBKE \Rightarrow \frac{DI}{KE} = \frac{BD}{BK}$ (4)

+ $ΔABK$ vuông tại A có:

$cos \hat{ABD} = \frac{AB}{BK} \Rightarrow c {os}^{2} \hat{ABD} = \frac{{AB}^{2}}{{BK}^{2}} = \frac{BD . BK}{{BK}^{2}} = \frac{BD}{BK}$ (5)

Từ (3), (4), (5) $\Rightarrow \frac{S_{BHD}}{S_{BKC}} = \frac{1}{4} . c {os}^{2} \hat{ABD}$ $\Rightarrow S_{BHD} = \frac{1}{4} S_{BKC} \cos^{2} \hat{ABD}$

Câu 5:

Cho biểu thức $P = x^{3} + y^{3} - 3 (x + y) + 1993$ . Tính giá trị biểu thức P với $x = \sqrt[3]{9 + 4 \sqrt{5}} + \sqrt[3]{9 - 4 \sqrt{5}}$ và $y = \sqrt[3]{3 + 2 \sqrt{2}} + \sqrt[3]{3 - 2 \sqrt{2}}$

Xem đáp án

Ta có: $x^{3} = 18 + 3 x \Rightarrow x^{3} - 3 x = 18$

$y^{3} = 6 + 3 y \Rightarrow y^{3} - 3 y = 6$

$\begin{array}{l} \Rightarrow P = x^{3} + y^{3} - 3 (x + y) + 1993 \\ = (x^{3} - 3 x) + (y^{3} - 3 y) + 1993 = 18 + 6 + 1993 = 2017 \end{array}$

Vậy P = 2017

với $x = \sqrt[3]{9 + 4 \sqrt{5}} + \sqrt[3]{9 - 4 \sqrt{5}}$ và $y = \sqrt[3]{3 + 2 \sqrt{2}} + \sqrt[3]{3 - 2 \sqrt{2}}$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi Giữa kì 1 Toán lớp 9 có đáp án

Đề thi Giữa kì 1 Toán lớp 9 có đáp án (Đề 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương