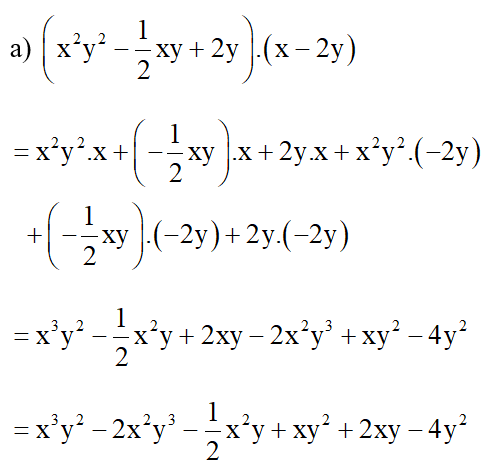Bài 2: Nhân đa thức với đa thức
-
6435 lượt thi
-
6 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Nhân đa thức xy – 1 với đa thức x3 – 2x – 6.
Xem đáp án
(
xy – 1).(x3 – 2x – 6) = xy.(x3 – 2x – 6) + (-1).(x3 – 2x – 6)
= xy.x3 + xy.(-2x) + xy.(-6) + (-1).x3 + (-1).(-2x) + (-1).(-6)
= x(1 + 3)y - x(1 + 1)y - 3xy - x3 + 2x + 6
= x4y-x2 y - 3xy - x3 + 2x + 6
= x4y - x3 - x2y - 3xy + 2x + 6
Câu 2:
Làm tính nhân:
a) (x + 3)(x2 + 3x – 5);
b) (xy – 1)(xy + 5).
Xem đáp án
a) (x + 3)(x2 + 3x – 5)
= x.(x2 + 3x – 5) + 3.(x2 + 3x – 5)
= x.x2 + x.3x + x.(–5) + 3.x2 + 3.3x + 3.(–5)
= x3 + 3x2 – 5x + 3x2 + 9x – 15
= x3 + (3x2 + 3x2) + (9x – 5x) – 15
= x3 + 6x2 + 4x – 15.
b) (xy – 1)(xy + 5)
= xy.(xy + 5) + (–1).(xy + 5)
= xy.xy + xy.5 + (–1).xy + (–1).5
= x2y2 + 5xy – xy – 5
= x2y2+ 4xy – 5.
Câu 3:
Viết biểu thức tính diện tích của một hình chữ nhật theo x và y, biết hai kích thước của hình chữ nhật đó là (2x + y) và (2x – y).
Áp dụng: Tính diện tích hình chữ nhật khi x = 2,5 mét và y = 1 mét.
Xem đáp án
Biểu thức tính diện tích hình chữ nhật là:
S = (2x + y).(2x – y)
= 2x.(2x – y) + y.(2x – y)
= 2x.2x + 2x.(–y) + y.2x + y.(–y)
= 4x2 – 2xy + 2xy – y2
= 4x2 – y2
Áp dụng : khi x = 2,5 mét và y = 1 mét
⇒ S = 4.2,52 – 12 = 4.6,25 – 1 = 25 – 1 = 24
Vậy diện tích của hình chữ nhật là: 24 mét vuông
Câu 4:
Làm tính nhân:
a) (x2 – 2x + 1)(x – 1)
b) (x3 – 2x2 + x – 1)(5- x)
Xem đáp án
a) (x2 – 2x + 1)( x – 1)
= x2.(x – 1) + (–2x).(x – 1) + 1.(x – 1)
= x2.x + x2.(– 1) + (– 2x).x + (–2x).(–1) + 1.x + 1.(–1)
= x3 – x2 – 2x2 + 2x + x – 1
= x3 – (x2 + 2x2) + (2x + x) – 1
= x3 – 3x2 + 3x – 1
b) (x3 – 2x2 + x – 1)(5 – x)
= (x3 – 2x2 + x – 1).5 + (x3 – 2x2 + x – 1).(–x)
= x3.5 + (–2x2).5 + x.5 + (–1).5 + x3.(–x) + (–2x2).(–x) + x.(–x) + (–1).(–x)
= 5x3 – 10x2 + 5x – 5 – x4 + 2x3 – x2 + x
= –x4 + (5x3 + 2x3) – (10x2 + x2) + (5x + x) – 5
= –x4 + 7x3 – 11x2 + 6x – 5
Ta có:
(x3 – 2x2 + x – 1).(x – 5)
= (x3 – 2x2 + x – 1).[–(5 – x)]
= – (x3 – 2x2 + x – 1).(5 – x)
= – (–x4 + 7x3 – 11x2 + 6x – 5)
= x4 – 7x3 + 11x2 – 6x + 5.
Kiến thức áp dụng
+ Để nhân hai đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
+ Với hai đa thức A, B bất kì ta luôn có : A.(–B) = –A.B
Câu 5:
Làm tính nhân:
Xem đáp án
b) (x2 – xy + y2)(x + y)
= (x2 – xy + y2).x + (x2 – xy + y2).y
= x2.x + (–xy).x + y2.x + x2.y + (–xy).y + y2.y
= x3 – x2y + xy2 + x2y – xy2 + y3
= x3 + y3 + (xy2 – xy2) + (xy2 – xy2)
= x3 + y3
Kiến thức áp dụng
+ Để nhân hai đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Câu 6:
Điền kết quả tính được vào bảng:
| Giá trị của x và y | Giá trị biểu thức (x – y)(x2 + xy + y2) |
| x = -10 ; y = 2 | |
| x = -1 ; y = 0 | |
| x = 2 ; y = -1 | |
| x = -0,5 ; y = 1,25 |
Xem đáp án
Ta có:
A = (x – y).(x2 + xy + y2)
= x.(x2 + xy + y2) + (–y).(x2 + xy + y2)
= x.x2 + x.xy + x.y2 + (–y).x2 + (–y).xy + (–y).y2
= x3 + x2y + xy2 – x2y – xy2 – y3
= x3 – y3 + (x2y – x2y) + (xy2 – xy2)
= x3 – y3.
Tại x = –10, y = 2 thì A = (–10)3 – 23 = –1000 – 8 = –1008
Tại x = –1 ; y = 0 thì A = (–1)3 – 03 = –1 – 0 = –1
Tại x = 2 ; y = –1 thì A = 23 – (–1)3 = 8 – (–1) = 9
Tại x = –0,5 ; y = 1,25 thì A = (–0,5)3 – 1,253 = –0,125 – 1,953125 = –2,078125
Vậy ta có bảng sau:
| Giá trị của x và y | Giá trị biểu thức (x – y)(x2 + xy + y2) |
| x = -10 ; y = 2 | -1008 |
| x = -1 ; y = 0 | -1 |
| x = 2 ; y = -1 | 9 |
| x = -0,5 ; y = 1,25 | -2,078125 |
Kiến thức áp dụng
+ Để nhân hai đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
+ Để tính giá trị biểu thức khi cho trước các giá trị của biến, ta nên rút gọn biểu thức trước khi thay giá trị .