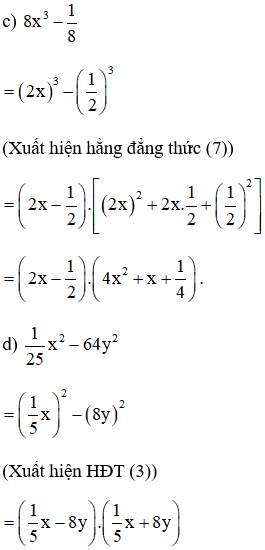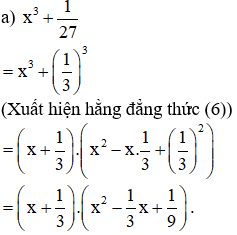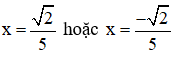6 câu hỏi trắc nghiệm thuộc Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức - hamchoi.vn

Giải SGK Toán 8 Đại số - Chương 1: Phép nhân và phép chia các đa thức

Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức

6443 lượt thi
6 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Phân tích các đa thức sau thành nhân tử

a) x³ + 3x² + 3x + 1;

b) (x + y)² - 9x².

a) x³ + 3x² + 3x + 1 = x³ + 3x².1 + 3x.1² + 1³ = (x + 1)³

b) (x + y)² – 9x² = (x + y)² – (3x)²

= (x + y + 3x)(x + y - 3x)

= (4x + y)(-2x + y)

Câu 2:

Tính nhanh: 105² – 25.

105² - 25 = 105² - 5²

= (105 + 5)(105 - 5)

= 110.100

= 11000

Câu 3:

Phân tích các đa thức sau thành nhân tử:

$a) x^{2} + 6 x + 9;$

$b) 10 x - 25 - x^{2};$

$c) 8 x^{3} - \frac{1}{8}$ ;

$d) \frac{1}{25} x^{2} - 64 y^{2} .$

a) x² + 6x + 9

= x² + 2.x.3 + 3²

(Xuất hiện hằng đẳng thức (1))

= (x + 3)²

b) 10x – 25 – x²

= –(–10x + 25 + x²)

= –(25 – 10x + x²)

= –(5² – 2.5.x + x²)

(Xuất hiện hằng đẳng thức (2) trong ngoặc)

= –(5 – x)²

Kiến thức áp dụng

Hằng đẳng thức cần nhớ:

(A + B)² = A² + 2AB + B² (1)

(A – B)² = A² – 2AB + B² (2)

A² – B² = (A – B)(A + B) (3)

A³ – B³ = (A – B)(A² + AB + B²) (7)

Câu 4:

Phân tích các đa thức sau thành nhân tử:

$a) x^{3} + \frac{1}{27};$

$b) {(a + b)}^{3} - {(a - b)}^{3};$

$c) {(a + b)}^{3} + {(a - b)}^{3};$

$d) 8 x^{3} + 12 x^{2} y + 6 x y^{2} + y^{3};$

$e) - x^{3} + 9 x^{2} - 27 x + 27 .$

b) (a + b)³ – (a – b)³

(Xuất hiện hằng đẳng thức (7))

= [(a + b) – (a – b)][(a + b)² + (a + b).(a – b) + (a – b)²]

= (a + b – a + b)(a² + 2ab + b² + a² – b²+ a² – 2ab + b²)

= 2b.(3a²+ b²)

c) (a + b)³ + (a – b)³

(Xuất hiện hằng đẳng thức (6))

= [(a + b) + (a – b)][(a + b)² – (a + b)(a –b) + (a – b)²]

= [(a + b) + (a – b)][(a² + 2ab + b²) – (a² – b²) + (a² – 2ab + b²)]

= (a + b + a – b)(a² + 2ab + b² – a² + b² + a² – 2ab + b²)

= 2a.(a² + 3b²)

d) 8x³ + 12x²y + 6xy² + y³

= (2x)³ + 3.(2x)².y + 3.2x.y² + y³

(Xuất hiện hằng đẳng thức (4))

= (2x + y)³

e) –x³ + 9x² – 27x + 27

= (–x)³ + 3.(–x)².3 + 3.(–x).3² + 3³

(Xuất hiện Hằng đẳng thức (4))

= (–x + 3)³

= (3 – x)³

Kiến thức áp dụng

(A + B)³ = A³ + 3A²B + 3AB² + B³ (4)

A³ + B³ = (A + B).(A² – AB + B²) (6)

A³ – B³ = (A – B)(A² + AB + B²) (7)

Câu 5:

Tìm x, biết:

$a) 2 - 25 x^{2} = 0;$

$b) x^{2} - x + \frac{1}{4} = 0$

a) Cách 1:

Cách 2:

2 – 25x² = 0

⇔ ${(\sqrt{2})}^{2}$ – (5x)² = 0

(Xuất hiện hằng đẳng thức (3))

⇔ ( $\sqrt{2}$ – 5x)( $\sqrt{2}$ + 5x) = 0

⇔ $\sqrt{2}$ – 5x = 0 hoặc $\sqrt{2}$ + 5x = 0

+ $\sqrt{2}$ – 5x = 0 ⇔ 5x = $\sqrt{2}$ ⇔ x = $\frac{\sqrt{2}}{5}$

+ $\sqrt{2}$ + 5x = 0 ⇔ 5x = – $\sqrt{2}$ ⇔ x = – $\frac{\sqrt{2}}{5}$

Vậy có hai giá trị của x thỏa mãn là

Kiến thức áp dụng

Hằng đẳng thức cần nhớ:

(A – B)² = A² – 2AB + B² (2)

A² – B² = (A – B)(A + B) (3)

Câu 6:

Tính nhanh:

a) 73² - 27² ;

b) 37² - 13² ;

c) 2002² - 2²

a) 73² – 27²

= (73 + 27)(73 – 27)

= 100.46

= 4600

b) 37² – 13²

= (37 + 13)(37 – 13)

= 50.24

= 100.12

= 1200

c) 2002² – 2²

= (2002 + 2)(2002 – 2)

= 2004 .2000

= 4008000

Kiến thức áp dụng

Hằng đẳng thức cần nhớ: A² – B² = (A – B)(A + B) (3)

Bắt đầu thi ngay

Bài thi liên quan

Các bài thi hot trong chương