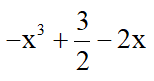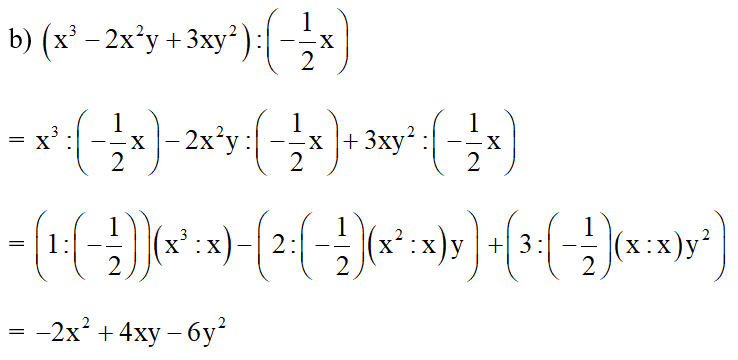Bài 11: Chia đa thức cho đơn thức
-
6445 lượt thi
-
6 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho đơn thức 3xy2.
- Hãy viết một đa thức có hạng tử đều chia hết cho 3xy2;
- Chia các hạng tử của đa thức đó cho 3xy2;
- Cộng các kết quả vừa tìm được với nhau.
Xem đáp án
(-9x3y6 + 18xy4 + 7x2 y2 ) : 3xy2
= (-9x3y6 : 3xy2 ) + (18xy4 : 3xy2 ) + (7x2y2 : 3xy2 )
= -3x2 y4 + 6y2 + 7/3 x
Câu 2:
a) Khi thực hiện phép chia (4x4 - 8x2 y2 + 12x5y) : (-4x2), bạn Hoa viết:
4x4 - 8x2 y2 + 12x5y = - 4x2(- x2 + 2y2 - 3x3y)
Nên (4x4 - 8x2 y2 + 12x5y) : (- 4x2) = - x2 + 2y2 - 3x3y.
Em hãy nhận xét xem bạn Hoa giải đúng hay sai.
b) Làm tính chia:
(20x4y - 25x2 y2 - 3x2y) : 5x2y.
Xem đáp án
a) Bạn Hoa giải đúng
b) 20x4y - 25x2y2 - 3x2y = 5x2y . (4x2 - 5y - 3/5)
Nên (20x4y - 25x2y2 - 3x2y) : 5x2y = 4x2 - 5y - 3/5
Câu 3:
Không làm tính chia, hãy xét xem đa thức A có chia hết đơn thức B không:
A = 15xy2 + 17xy3 + 18y2
B = 6y2
Xem đáp án
Nhận thấy:
15xy2 chia hết cho 6y2
17xy3 chia hết cho 6y2
18y2 chia hết cho 6y2
Vậy A = 15xy2 + 17xy3 + 18y2 chia hết cho 6y2 hay A chia hết cho B.
Kiến thức áp dụng
Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
Đa thức A (đã được rút gọn) chia hết cho đơn thức B nếu mỗi hạng tử của đa thức A đều chia hết cho đơn thức B.
Câu 4:
Làm tính chia:
.
Xem đáp án
a) (–2x5 + 3x2 – 4x3) : 2x2
= (–2x5) : 2x2 + 3x2 : 2x2 + (–4x3) : 2x2
= [(–2) : 2].(x5 : x2) + (3 : 2).(x2 : x2) + [(–4) : 2].(x3 : x2)
= 
c) (3x2y2 + 6x2y3 – 12xy) : 3xy
= (3x2y2 : 3xy) + (6x2y3 : 3xy) + ( –12xy : 3xy)
= (3 : 3).(x2 : x).(y2 : y) + (6 : 3).(x2 : x).(y3 : y) + (–12 : 3).(x : x).(y : y)
= 1.x.y + 2.xy2 + (–4).1.1
= xy + 2xy2 – 4
Kiến thức áp dụng
– Để chia đa thức A cho đơn thức B, ta chia từng hạng tử của đa thức A cho đơn thức B rồi cộng các kết quả với nhau.
– Muốn chia đơn thức A cho đơn thức B ta làm như sau :
+ Chia hệ số của đơn thức A cho hệ số của đơn thức B
+ Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
+ Nhân các kết quả vừa tìm được với nhau.
Câu 5:
Làm tính chia:
[3(x – y)4 + 2(x – y)3 – 5(x – y)2] : (y – x)2
(Gợi ý : Có thể đặt x – y = z rồi áp dụng qui tắc chia đa thức cho đơn thức)
Xem đáp án
Ta có : (y – x)2 = [–(x – y)2] = (x – y)2.
Đặt x – y = z, Khi đó biểu thức trở thành :
(3z4 + 2z3 – 5z2) : z2
= 3z4 : z2 + 2z3 : z2 + (–5z2) : z2
= 3.(z4 : z2) + 2.(z3 : z2) + (–5).(z2 : z2)
= 3.z2 + 2.z + (–5).1
= 3z2 + 2z – 5
Thay trả lại z = x – y ta được kết quả biểu thức bằng : 3(x – y)2 + 2(x – y) – 5.
Kiến thức áp dụng
– Để chia đa thức A cho đơn thức B, ta chia từng hạng tử của đa thức A cho đơn thức B rồi cộng các kết quả với nhau.
– Muốn chia đơn thức A cho đơn thức B ta làm như sau :
+ Chia hệ số của đơn thức A cho hệ số của đơn thức B
+ Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
+ Nhân các kết quả vừa tìm được với nhau.
Câu 6:
Ai đúng, ai sai ?
Khi giải bài tập: "Xét xem đa thức A = 5x4 – 4x3 + 6x2y có chia hết cho đơn thức B = 2x2 hay không ?".
Hà trả lời: "A không chia hết cho B vì 5 không chia hết cho 2".
Xem đáp án
Lời giải của bạn Hà sai, lời giải của bạn Quang đúng.
Vì 5x4 chia hết cho 2x2;
–4x3 chia hết cho 2x2;
6x2y chia hết cho 2x2
Do đó A = 5x4 – 4x3 + 6x2y chia hết cho 2x2 hay A chia hết cho B.
Chú ý: Đơn thức A chia hết cho đơn thức B nếu tìm được đơn thức Q sao cho A=B.Q
Ví dụ : Cho hai đơn thức A= 2x2y3; B = 7xy
Khi đó với đơn thức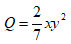 
thì A=B.Q
Do đó, đơn thức A chia hết cho đơn thức B.
Kiến thức áp dụng
Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
Đa thức A (đã được rút gọn) chia hết cho đơn thức B nếu mỗi hạng tử của đa thức A đều chia hết cho đơn thức B.