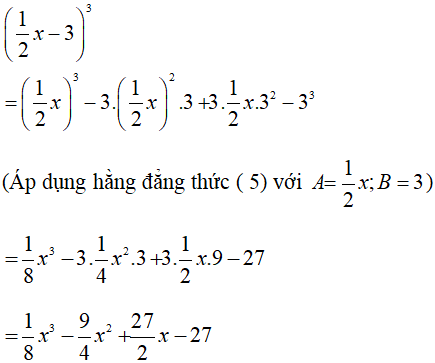Bài 4: Những hằng đẳng thức đáng nhớ (tiếp)
-
6439 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tính (a + b)(a + b)2 (với a, b là hai số tùy ý).
Xem đáp án
(a + b)(a + b)2 = (a + b)(a2 + 2ab + b2 )
= a(a2 + 2ab + b2 ) + b(a2 + 2ab + b2 )
= a3 + 2a2 b + ab2 + ba2 + 2ab2 + b3
= a3 + 3a2 b + 3ab2 + b3
Câu 2:
Phát biểu hằng đẳng thức (4) bằng lời.
Xem đáp án
Lập phương của tổng hai biểu thức bằng tổng của lập phương biểu thức thứ nhất, ba lần tích của bình phương biểu thức thứ nhất và biểu thức thứ hai, ba lần tích của biểu thức thứ nhất và bình phương biểu thức thứ hai và lập phương biểu thức thứ hai
Câu 3:
Tính [a + (-b)]3 (với a, b là hai số tùy ý).
Xem đáp án
Áp dụng hằng đẳng thức (4) ta có:
[a + (-b)]3 = a3 + 3a2 (-b) + 3a(-b)2 + (-b)3
= a3 - 3a2b + 3ab2 - b3
Câu 4:
Phát biểu hằng đẳng thức (5) bằng lời.
Xem đáp án
Lập phương của hiệu hai biểu thức bằng lập phương biểu thức thứ nhất trừ đi ba lần tích của bình phương biểu thức thứ nhất và biểu thức thứ hai, sau đó cộng ba lần tích của biểu thức thứ nhất và bình phương biểu thức thứ hai rồi trừ đi lập phương biểu thức thứ hai.
Câu 5:
Tính:
Xem đáp án
a) (2x2 + 3y)3 = (2x2)3 + 3.(2x2)2.3y + 3.2x2.(3y)2 + (3y)3
(Áp dụng HĐT (4) với A = 2x2, B = 3y)
= 8x6 + 3.4x4.3y + 3.2x2.9y2 + 27y3
= 8x6 + 36x4y + 54x2y2 + 27y3
b)
Kiến thức áp dụng
Hằng đẳng thức cần nhớ:
(A + B)3 = A3 + 3A2B + 3AB2 + B3 (4)
(A – B)3 = A3 – 3A2B + 3AB2 – B3 (5)
Câu 6:
Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu:
a) –x3 + 3x2 – 3x + 1
b) 8 – 12x + 6x2 – x3
Xem đáp án
a) –x3 + 3x2 – 3x + 1
= (–x)3 + 3.(–x)2.1 + 3.(–x).1 + 13
= (–x + 1)3 (Áp dụng HĐT (4) với A = –x và B = 1)
b) 8 – 12x + 6x2 – x3
= 23 – 3.22.x + 3.2.x2 – x3
= (2 – x)3 (Áp dụng HĐT (5) với A = 2 và B = x)
Kiến thức áp dụng
Hằng đẳng thức cần nhớ:
(A + B)3 = A3 + 3A2B + 3AB2 + B3 (4)
(A – B)3 = A3 – 3A2B + 3AB2 – B3 (5)
Câu 7:
Tính giá trị của biểu thức:
a) x3 + 12x2 + 48x + 64 tại x = 6
b) x3 – 6x2 + 12x – 8 tại x = 22
Xem đáp án
a) x3 + 12x2 + 48x + 64 = x3 + 3.x2.4 + 3.x.42 + 43 = (x + 4)3
Tại x = 6, giá trị biểu thức bằng (6 + 4)3 = 103 = 1000.
b) x3 – 6x2 + 12x – 8 = x3 – 3.x2.2 + 3.x.22 – 23 = (x – 2)3
Tại x = 22, giá trị biểu thức bằng (22 – 2)3 = 203 = 8000.
Kiến thức áp dụng
Hằng đẳng thức cần :
(A + B)3 = A3 + 3A2B + 3AB2 + B3 (4)
(A – B)3 = A3 – 3A2B + 3AB2 – B3 (5)