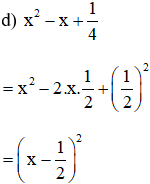Bài 3: Những hằng đẳng thức đáng nhớ
-
6437 lượt thi
-
11 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Với a và b là hai số bất kì, thức hiện phép tính (a + b)(a + b).
Xem đáp án
(a + b)(a + b) = a(a + b) + b(a + b)
= a2 + ab + ba + b2
= a2 + 2ab + b2
Câu 2:
Phát biểu hằng đẳng thức (1) bằng lời.
Xem đáp án
Bình phương của tổng hai biểu thức bằng tổng của bình phương biểu thức thứ nhất, bình phương biểu thức thứ hai và hai lần tích hai biểu thức đó
Câu 3:
Tính [a + (-b)]2 (với a, b là các số tùy ý).
Xem đáp án
Áp dụng hằng đẳng thức (1) ta có:
[a + (-b)]2 = a2 + 2.a.(-b) + (-b)2 = a2 - 2ab + b2
Câu 4:
Phát biểu hằng đẳng thức (2) bằng lời.
Xem đáp án
Bình phương của hiệu hai biểu thức bằng tổng của bình phương biểu thức thứ nhất và bình phương biểu thức thứ hai, sau đó trừ đi hai lần tích hai biểu thức đó
Câu 5:
Thực hiện phép tính (a + b)(a – b) (với a, b là các số tùy ý).
Xem đáp án
(a + b)(a – b) = a(a – b) + b(a – b)
= a2 - ab + ba - b2
= a2 - b2
Câu 6:
Phát biểu hằng đẳng thức (3) bằng lời.
Xem đáp án
Hiệu của bình phương hai biểu thức bằng tích của tổng hai biểu thức và hiệu hai biểu thức.
Câu 7:
Ai đúng, ai sai ?
Đức viết:
x2 – 10x + 25 = (x - 5)2.
Thọ viết:
x2 – 10x + 25 = (5 - x)2.
Hương nêu nhận xét: Thọ viết sai, Đức viết đúng.
Sơn nói: Qua ví dụ trên mình rút ra được một hằng đẳng thức rất đẹp !
Hãy nêu ý kiến của em. Sơn rút ra được hằng đẳng thức nào ?
Xem đáp án
- Đức và Thọ đều viết đúng;
Hương nhận xét sai;
- Sơn rút ra được hằng đẳng thức là: (x - 5)2 = (5 - x)2
Câu 8:
Viết các biểu thức sau đây dưới dạng bình phương của một tổng hoặc một hiệu:
Xem đáp án
a) x2 + 2x + 1
= x2 + 2.x.1 + 12
= (x + 1)2 (Áp dụng hằng đẳng thức (1) với A = x và B = 1)
b) 9x2 + y2 + 6xy
= 9x2 + 6xy + y2
= (3x)2 + 2.3x.y + y2
= (3x + y)2 (Áp dụng hằng đẳng thức (1) với A = 3x và B = y)
c) 25a2 + 4b2 – 20ab
= 25a2 – 20ab + 4b2
= (5a)2 – 2.5a.2b + (2b)2
= (5a – 2b)2 (Áp dụng hằng đẳng thức (2) với A = 5a và B = 2b)
(Áp dụng hằng đẳng thức (2) với A = x và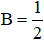 
)
Kiến thức áp dụng
+ Hằng đẳng thức:
(A + B)2 = A2 + 2AB + B2 (1)
(A – B)2 = A2 – 2AB + B2 (2)
+ Lưu ý : (A – B)2 = (B – A)2.
Câu 9:
Chứng minh rằng: (10a + 5)2 = 100a . a(a + 1) + 25
Từ đó em hãy nêu cách tính nhẩm bình phương của một số tự nhiên có tận cùng bằng chữ số 5.
Áp dụng để tính: 252; 352; 652; 752
Xem đáp án
Ta có:
(10a + 5)2 = (10a)2 + 2.10a.5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25
Đặt A = a.(a + 1). Khi đó ta có:
Do vậy, để tính bình phương của một số tự nhiên có dạng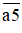 
, ta chỉ cần tính tích a.(a + 1) rồi viết 25 vào đằng sau kết quả vừa tìm được.
Áp dụng:
252 = (10.2 + 5)2 do đó a = 2 ⇒ A = a(a + 1) = 2.3 = 6 sau đó viết 25 vào đằng sau ta được 625. Vậy 252 = 625
352 = (10.3 + 5)2 do đó a = 3 ⇒ A = a(a + 1) = 3.4 = 12 sau đó viết 25 vào đằng sau ta được 1225. Vậy 352 = 1225
652 = (10.6 + 5)2 do đó a = 6 ⇒ A = a(a + 1) = 6.7 = 42 sau đó viết 25 vào đằng sau ta được 4225. Vậy 652 = 4225
752 = (10.7 + 5)2 do đó a = 7 ⇒ A = a(a + 1) = 7.8 = 56 sau đó viết 25 vào đằng sau ta được 5625. Vậy 752 = 5625
Kiến thức áp dụng
Hằng đẳng thức : (A + B)2 = A2 + 2AB + B2.
Câu 10:
Hãy tìm cách giúp bạn An khôi phục lại những hằng đẵng thức bị mực làm nhòe đi một số chỗ:
a) x2 + 6xy + ... = ( ... + 3y)2
b) ... - 10xy + 25y2 = ( ... - ...)2
Hãy nêu một đề bài tương tự.
Xem đáp án
a) Dễ dàng nhận thấy đây là hằng đẳng thức (1) với
A = x ;
2.AB = 6xy ⇒ B = 3y.
Vậy ta có hằng đẳng thức:
x2 + 2.x.3y + (3y)2 = (x + 3y)2
hay x2 + 6xy + 9y2 = (x + 3y)2
b) Nhận thấy đây là hằng đẳng thức (2) với :
B2 = 25y2 = (5y)2 ⇒ B = 5y
2.AB = 10xy = 2.x.5y ⇒ A = x.
Vậy ta có hằng đẳng thức : x2 – 10xy + 25y2 = (x – 5y)2
c) Đề bài tương tự:
4x2 + 4xy + ... = (... + y2)
... – 8xy + y2 = ( ...– ...)2
Kiến thức áp dụng
Hằng đẳng thức:
(A + B)2 = A2 + 2AB + B2 (1)
(A – B)2 = A2 – 2AB + B2 (2)
Câu 11:
Đố. Tính diện tích phần hình còn lại mà không cần đo.
Từ một miếng tôn hình vuông có cạnh bằng a + b, bác thợ cắt đi một miếng cũng hình vuông có cạnh bằng a – b (cho a > b). Diện tích phần hình còn lại là bao nhiêu? Diện tích phần hình còn lại có phụ thuộc vào vị trí cắt không?
Xem đáp án
Diện tích của miếng tôn ban đầu là (a + b)2.
Diện tích của miếng tôn phải cắt là : (a – b)2.
Phần diện tích còn lại (a + b)2 – (a – b)2.
Ta có: (a + b)2 – (a – b)2
= (a2 + 2ab + b2) – ( a2 – 2ab + b2 )
= a2 + 2ab + b2 – a2 + 2ab – b2
= 4ab
Hoặc: (a + b)2 – (a – b)2
= [(a + b) + (a – b)].[(a + b) – (a – b)] (Áp dụng hằng đẳng thức (3))
= 2a.2b
= 4ab.
Vậy phần diện tích hình còn lại là 4ab và không phụ thuộc vào vị trí cắt.
Kiến thức áp dụng
Hằng đẳng thức cần nhớ
(A + B)2 = A2 + 2AB + B2 (1)
(A – B)2 = A2 – 2AB + B2 (2)
A2 – B2 = (A + B)(A – B) (3)