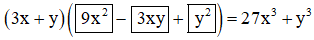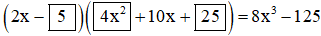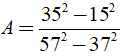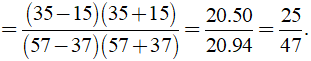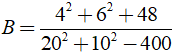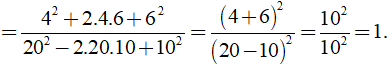Bài 5: Những hằng đẳng thức đáng nhớ (tiếp)
-
4749 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tính (a + b)(a2 – ab + b2) (với a, b là hai số tùy ý).
Xem đáp án
(a + b)(a2 – ab + b2 ) = a(a2 – ab + b2 ) + b(a2 – ab + b2 )
= a3 – a2b + ab2 + ba2 – ab2 + b3
= a3 + b3
Câu 2:
Phát biểu hằng đẳng thức (6) bằng lời.
Xem đáp án
Tổng của lập phương hai biểu thức bằng tích của tổng hai biểu thức và bình phương thiếu của hiệu hai biểu thức đó
Câu 3:
Tính (a - b)(a2 + ab + b2 ) (với a, b là hai số tùy ý).
Xem đáp án
(a - b)(a2 + ab + b2 ) = a(a2 + ab + b2 ) - b(a2 + ab + b2 )
= a3 + a2 b + ab2 - ba2 - ab2 - b3
= a3 - b3
Câu 4:
Phát biểu hằng đẳng thức (7) bằng lời.
Xem đáp án
Hiệu của lập phương hai biểu thức bằng tích của hiệu hai biểu thức và bình phương thiếu của tổng hai biểu thức đó
Câu 5:
Rút gọn các biểu thức sau:
a) (x + 3)(x2 – 3x + 9) – (54 + x3)
b) (2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)
Xem đáp án
a) (x + 3)(x2 – 3x + 9) – (54 + x3)
= x3 + 33 – (54 + x3) (Áp dụng HĐT (6) với A = x và B = 3)
= x3 + 27 – 54 – x3
= –27
b) (2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)
= (2x + y)[(2x)2 – 2x.y + y2] – (2x – y)[(2x)2 + 2x.y + y2]
= [(2x)3 + y3] – [(2x)3 – y3]
= (2x)3 + y3 – (2x)3 + y3
= 2y3
Kiến thức áp dụng
Hằng đẳng thức cần nhớ:
A3 + B3 = (A + B)(A2 – AB + B2) (6)
A3 – B3 = (A – B)(A2 + AB + B2) (7)
Câu 6:
Chứng minh rằng:
a) a3 + b3 = (a + b)3 – 3ab(a + b)
b) a3 – b3 = (a – b)3 + 3ab(a – b)
Áp dụng: Tính a3 + b3, biết a.b = 6 và a + b = -5
Xem đáp án
a) Biến đổi vế phải ta được:
(a + b)3 – 3ab(a + b)
= a3 + 3a2b + 3ab2 + b3 – 3a2b – 3ab2
= a3 + b3
Vậy a3 + b3 = (a + b)3 – 3ab(a + b)
b) Biến đổi vế phải ta được:
(a – b)3 + 3ab(a – b)
= a3 – 3a2b + 3ab2 – b3 + 3a2b – 3ab2
= a3 – b3
Vậy a3 – b3 = (a – b)3 + 3ab(a – b)
– Áp dụng: Với ab = 6, a + b = –5, ta được:
a3 + b3 = (a + b)3 – 3ab(a + b) = (–5)3 – 3.6.(–5) = –53 + 3.6.5 = –125 + 90 = –35
Kiến thức áp dụng
Hằng đẳng thức cần nhớ:
(A + B)3 = A3 + 3A2B + 3AB2 + B3 (4)
(A – B)3 = A3 – 3A2B + 3AB2 + B3 (5)
Câu 7:
Điền các đơn thức thích hợp vào ô trống:
Xem đáp án
a) Ta có thể nhận thấy đây là hằng đẳng thức (6).
27x3 + y3
= (3x)3 + y3
= (3x + y)[(3x)2 – 3x.y + y2] (Áp dụng HĐT (6) với A = 3x, B = y)
= (3x + y)(9x2 – 3xy + y2)
Vậy ta cần điền :
b) Ta có thể nhận thấy đây là hằng đẳng thức (7)
8x3 – 125
= (2x)3 – 53
= (2x – 5).[(2x)2 + (2x).5 + 52] (Áp dụng HĐT (7) với A = 2x, B = 5)
= (2x – 5).(4x2 + 10x + 25)
Vậy ta cần điền :
Kiến thức áp dụng
Hằng đẳng thức cần nhớ:
A3 + B3 = (A + B)(A2 – AB + B2) (6)
A3 – B3 = (A – B)(A2 + AB + B2) (7)
Câu 8:
Tính nhanh:
a) 342 + 662 + 68.66
b) 742 + 242 – 48.74
Xem đáp án
a) 342 + 662 + 68.66
a) 342 + 68.66 + 662
= 342 + 2.34.66 + 662
= (34 + 66)2
= 1002
= 10000
b) 742 + 242 – 48.74
b) 742 – 48.74 + 242
= 742 – 2.74.24 + 242
= (74 – 24)2
= 502
= 2500
Kiến thức áp dụng
Các hằng đẳng thức cần nhớ :
(A + B)2 = A2 + 2AB + B2 (1)
(A – B)2 = A2 – 2AB + B2 (2)
Câu 9:
Tính giá trị của các biểu thức sau:
Xem đáp án
a) Ta có: 
(áp dụng hằng đẳng thức a2 - b2 = ( a + b )( a - b ) )
Vậy A = 25/47.
b) Ta có 
(áp dụng hằng đẳng thức ( a + b )2 = a2 + 2ab + b2; ( a - b )2 = a2 - 2ab + b2 )
Vậy B = 1.
Bài 2: Tìm x biết
a) ( x - 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 - x ) = 0.
b) ( x + 1 )3 - ( x - 1 )3 - 6( x - 1 )2 = - 10.
Hướng dẫn:
a) Áp dụng các hằng đẳng thức ( a - b )( a2 + ab + b2 ) = a3 - b3.
( a - b )( a + b ) = a2 - b2.
Khi đó ta có ( x - 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 - x ) = 0.
⇔ x3 - 33 + x( 22 - x2 ) = 0 ⇔ x3 - 27 + x( 4 - x2 ) = 0
⇔ x3 - x3 + 4x - 27 = 0
⇔ 4x - 27 = 0 ⇔ x = 27/4.
Vậy giá trị x cần tìm là x= 27/4 .
b) Áp dụng hằng đẳng thức ( a - b )3 = a3 - 3a2b + 3ab2 - b3
( a + b )3 = a3 + 3a2b + 3ab2 + b3
( a - b )2 = a2 - 2ab + b2
Khi đó ta có: ( x + 1 )3 - ( x - 1 )3 - 6( x - 1 )2 = - 10.
⇔ ( x3 + 3x2 + 3x + 1 ) - ( x3 - 3x2 + 3x - 1 ) - 6( x2 - 2x + 1 ) = - 10
⇔ 6x2 + 2 - 6x2 + 12x - 6 = - 10
⇔ 12x = - 6 ⇔ x = - 1/2.
Vậy giá trị x cần tìm là x= - 1/2
Câu 10:
Tìm x biết
a) ( x - 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 - x ) = 0.
b) ( x + 1 )3 - ( x - 1 )3 - 6( x - 1 )2 = - 10.
Xem đáp án
a) Áp dụng các hằng đẳng thức ( a - b )( a2 + ab + b2 ) = a3 - b3.
( a - b )( a + b ) = a2 - b2.
Khi đó ta có ( x - 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 - x ) = 0.
⇔ x3 - 33 + x( 22 - x2 ) = 0 ⇔ x3 - 27 + x( 4 - x2 ) = 0
⇔ x3 - x3 + 4x - 27 = 0
⇔ 4x - 27 = 0 ⇔ x = 27/4.
Vậy giá trị x cần tìm là x= 27/4 .
b) Áp dụng hằng đẳng thức ( a - b )3 = a3 - 3a2b + 3ab2 - b3
( a + b )3 = a3 + 3a2b + 3ab2 + b3
( a - b )2 = a2 - 2ab + b2
Khi đó ta có: ( x + 1 )3 - ( x - 1 )3 - 6( x - 1 )2 = - 10.
⇔ ( x3 + 3x2 + 3x + 1 ) - ( x3 - 3x2 + 3x - 1 ) - 6( x2 - 2x + 1 ) = - 10
⇔ 6x2 + 2 - 6x2 + 12x - 6 = - 10
⇔ 12x = - 6 ⇔ x = - 1/2.
Vậy giá trị x cần tìm là x= - 1/2