Chuyên đề 8: Hình học (có đáp án)
-
3702 lượt thi
-
191 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
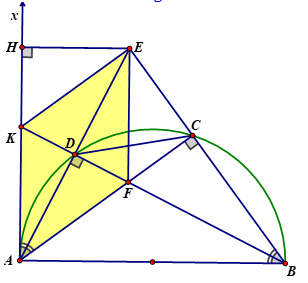
a) Ta có (góc nội tiếp chắn nửa đường tròn)
Suy ra (kề bù)
Xét tứ giác AHEC ta có: , suy ra tứ giác AHEC nội tiếp đường tròn đường kính AE (tổng hai góc đối diện bằng 180o)Câu 2:
b) Chứng minh
 Xem đáp án
Xem đáp án
b) Ta có ABCD nội tiếp nên (1) (cùng nhìn cạnh DC).
Lại có: (góc nội tiếp).
(góc tạo bởi tiếp tuyến và dây cung).
Suy ra .
Mà (do ADlà phân giác).
Suy ra (2)
Từ (1) và (2) suy ra
Câu 3:
c) Chứng minh tam giác ABE cân
 Xem đáp án
Xem đáp án
c) Xét và có:
(góc nội tiếp chắn nửa đường tròn – kề bù).
BD chung.
(cmt).
(g-c-g).
(tương ứng).
cân tại ![]()
Câu 4:
 Xem đáp án
Xem đáp án
d) Theo câu c) là trung điểm AE (3)
Xét và có:
(góc nội tiếp chắn nửa đường tròn – kề bù).
AD chung.
(do ADlà phân giác).
(g-c-g)
(tương ứng).
là trung điểm KF (4)
Từ (3) và (4) ta có AKEF là hình bình hành (tứ giác có các đường chéo cắt nhau tại trung điểm mỗi đường).
Mà là hình thoi.Câu 5:
Cho nửa đường tròn (O;R) đường kính AB. Trên OA lấy điểm H (H khác O, H khác A). Qua H dựng đường thẳng vuông góc với AB, đường thẳng này cắt nửa đường tròn tại C. Trên cung BC lấy điểm M (M khác B, M khác C). Dựng CK vuông góc với AM tại K.
a) Chứng minh tứ giác ACKH nội tiếp đường tròn Xem đáp án
Xem đáp án
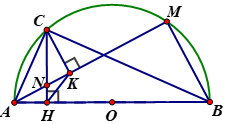
Ta có Tứ giác ACHK nội tiếp đường tròn đường kính AC
Câu 7:
c) Gọi N là giao điểm của AM và CH. Tính theo R giá trị biểu thức
 Xem đáp án
Xem đáp án
Ta có
Do đó (g.g)
C thuộc nửa đường tròn đường kính AB nên tam giác ABC vuông tại .
Vậy
Câu 8:
Cho nhọn (AB<AC) nội tiếp đường tròn (O). Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau tại D. OD cắt BC tại E. Qua D vẽ đường thẳng song song với AB, đường thẳng này cắt AC tại K. đường thẳng OK cắt AB tại F. Tính tỉ số diện tích
 Xem đáp án
Xem đáp án
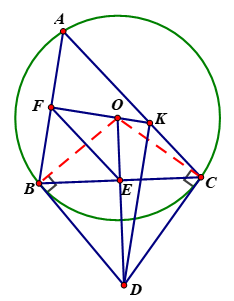
Ta có (cùng chắn ), (đồng vị)
nội tiếp.
Mà: nên các điểm B, C, D thuộc đường tròn đường kính OD
cũng thuộc đường tròn đường kính OD
là trung điểm của AB.
Do là trung trực của BC
là trung điểm của BC
Hai tam giác BEF và BAC đồng dạng có tỉ lệ đồng dạng là
Câu 9:
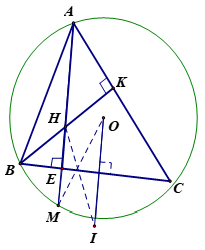
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn (C) tâm O bán kính R. Hai đường cao AE và BK tam giác ABC cắt nhau tại H (với E thuộc BC, K thuộc AC).
1. Chứng minh rằng tứ giác ABEK nội tiếp được trong một đường tròn.
 Xem đáp án
Xem đáp án
Câu 10:
2. Chứng minh CE.CB=CK.CA
 Xem đáp án
Xem đáp án
2. Xét hai tam giác vuông và , chúng có chung góc C nên
(dpcm).
Câu 11:
3. Chứng minh .
 Xem đáp án
Xem đáp án
3. Tam giác OAC cân tại O nên . Mà tam giác ABC nhọn nên O nằm trong tam giác ABC, do đó .
Tam giác ABE vuông tại E nên (2).
Từ (1) và (2) (dpcm).
Câu 12:
 Xem đáp án
Xem đáp án
4. Gọi M là giao điểm của đường thẳng AE với đường tròn (C). Ta có ( cùng chắn cung MC). Mà ( cùng phụ với ) nên hay BE là phân giác của .Tam giác HBM có BE vừa là đường cao, đường phân giác góc B nên cân tại B và BE là trung trực của HM. Gọi I là điểm đối xứng với O qua đường thẳng BC(O và BC cố định cố định). Khi đó tứ giác HOIM là hình thang cân vì nhận BC là trục đối xứng=MO=R hay H luôn cách điểm cố định I một khoảng R không đổi nên H thuộc đường tròn tâm I bán kính R. Do đó r=R=3cm.
Câu 13:
Cho có ba góc nhọn (AB<AC), dựng AH vuông góc với BC tại điểm H. Gọi M, N theo thứ tự là hình chiếu vuông góc của H trên AB, AC. Đường thẳng MN cắt đường thẳng BC tại điểm D. Trên nửa mặt phẳng bờ CD chứa điểm A, vẽ nửa đường tròn đường kính CD. Qua B kẻ đường thẳng vuông góc với CD, cắt nửa đường tròn trên tại điểm E.
a. Chứng minh tứ giác AMHN là tứ giác nội tiếp.
 Xem đáp án
Xem đáp án
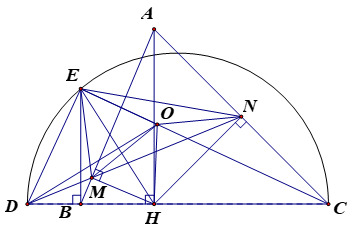
a. Vì M, N lần lượt là hình chiếu vuông góc của H trên AB, AC .
Xét tứ giác AMHN có: .
Do đó tứ giác AMHN nội tiếp đường trònCâu 14:
b) Chứng minh
 Xem đáp án
Xem đáp án
b. Vì (gt), (vì ) EB//AH.
(hai góc so le trong) (1)
Tứ giác AMHN nội tiếp (cmt) (hai góc nội tiếp cùng chắn ) (2)
Từ (1) và (2) suy ta , hay .
Câu 15:
 Xem đáp án
Xem đáp án
c. Ta có: (hai góc đối đỉnh) (3)
Tứ giác AMHN nội tiếp (cmt) (hai góc nội tiếp cùng chắn ) (4)
vuông tại H có (gt) (cùng phụ với )
Hay (5)
Từ (3), (4) và (5) suy ra .
Xét và có: chung; (cmt)
(g.g) . (6)
Câu 16:
 Xem đáp án
Xem đáp án
d. nội tiếp đường tròn đường kính CD vuông tại E.
Áp dụng hệ thức lượng trong vuông tại E, , ta có: . (7)
Từ (6) và (7) suy ra .
Xét và có: chung; (cmt)
(c.g.c) (2 góc tương ứng).
Xét (O) có: và tia EM nằm giữa hai tia ED và EN.
Do đó DE là tiếp tuyến của (O).
Câu 17:
 Xem đáp án
Xem đáp án
Kẻ , (Hệ quả ĐL Talet).
Lại có .
Chứng minh tương tự, ta có ; .
Suy ra .
Đặt ; ; thì x, y, z > 0 và x+y+z=1.
Theo đề bài:
Hay:
. (*)
Bất đẳng thức (*) hiển nhiên đúng với x, y, z>0.
Dấu bằng xảy ra khi , hay là trọng tâm .
Vậy .
Câu 18:
 Xem đáp án
Xem đáp án
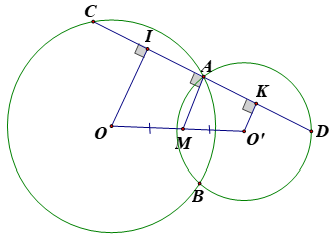
Kẻ tại I, tại K, khi đó ta có
(tính chất của bán kính vuông góc với dây cung thì đi qua trung điểm của dây cung đó).
Ta có: nên tứ giác là hình thang.
Mà và M là trung điểm của OO'
là trung điểm của
Từ đó suy ra AC=AD(đpcm).
Câu 19:
Cho đường tròn (O) đường kính AB, cung năm cùng phía đối với AB(D thuộc cung nhỏ ). Gọi E là giao điểm của AC và BD, F là giao điểm của AD và BC.
a. Tính góc khi số đo cung bằng 80o
 Xem đáp án
Xem đáp án
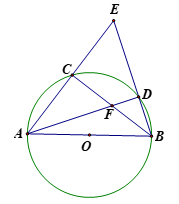
a. sđ , .
là góc có đỉnh bên trong đường tròn chắn 2 cung AB, CD nên ta có:
Câu 20:
b. Tính số đo cung khi góc .
 Xem đáp án
Xem đáp án
b. .
là góc có đỉnh bên ngoài đường tròn chắn 2 cung AB, CD nên:
Câu 21:
Cho tam giác nhọn ABC(AB<AC). Đường tròn tâm (O) đường kính BC cắt AC, AB lần lượt tại D và E. H là giao điểm của BD và CE, K là giao điểm của DE và AH, I là giao điểm của AH và BC, M là trung điểm của AH. Chứng minh rằng:
 Xem đáp án
Xem đáp án
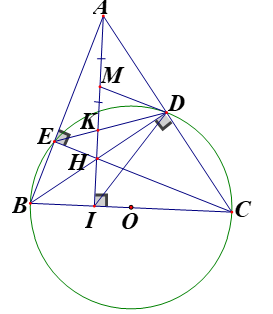
Ta có là các góc nội tiếp chắn nửa đường tròn tâm O nên
Mà BD và CE cắt nhau tại H nên ta suy ra H là trực tâm của tam giác ABC.
Suy ra
Ta có nên CDHI là tứ giác nội tiếp đường tròn đường kính HC.
Suy ra (góc nội tiếp cùng chắn cung DH của đường tròn đường kính HC).
Hay
Tương tự, ta chứng minh được tứ giác AEIH nội tiếp đường tròn tâm M
().
(vì MD=MA) và
(cùng chắn cung EH của đường tròn tâm M)
Vậy
Xét 2 tam giác MDK và MID có:
là góc chung,
(g.g)
(đpcm).
Câu 22:
Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB với đường tròn (A, B là hai tiếp điểm). Lấy điểm C trên cung nhỏ AB, (C không trùng với A và B). Từ điểm C kẻ CD vuông góc với AB, CE vuông góc với MA, CF vuông góc với MB . Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. Chứng minh rằng
1) Tứ giác ADCE nội tiếp một đường tròn.
 Xem đáp án
Xem đáp án
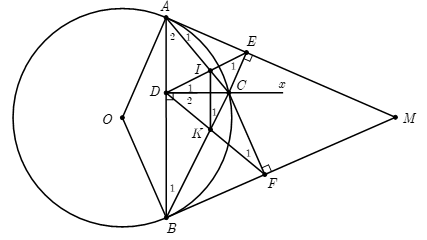
1) Chứng minh rằng Tứ giác ADCE nội tiếp một đường tròn.
Ta có do đó, tứ giác ADCE nội tiếp.
Câu 23:
2) Hai tam giác CDE và CFD đồng dạng
 Xem đáp án
Xem đáp án
2) Chứng minh rằng Hai tam giác CDE và CFD đồng dạng.
Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác ADCE, BDCF nội tiếp nên
Mà AM là tiếp tuyến của đường tròn (O) nên
Chứng minh tương tự Do đó,
Câu 24:
 Xem đáp án
Xem đáp án
3) Chứng minh rằng Tia đối của tia CD là tia phân giác góc ECF
Gọi Cx là tia đối của tia CD
Do các tứ giác nội tiếp nên
Mà nên Cx là phân giác góc
Câu 25:
 Xem đáp án
Xem đáp án
4) Chứng minh rằng Đường thẳng IK song song với đường thẳng AB
Theo chứng minh trên
Mà
Do đó, tứ giác CIKD nội tiếp mà
Câu 26:
Cho đường tròn tâm O, đường kính AB. Trên tiếp tuyến của đường tròn (O) tại A lấy điểm M(M khác A ). Từ M vẽ tiếp tuyến thứ hai MC với đường tròn (O) (C là tiếp điểm). Kẻ (),MB cắt đường tròn (O) tại điểm thứ hai là K và cắt CH tại N. Chứng minh rằng:
a) Tứ giác AKNH nội tiếp trong một đường tròn.
 Xem đáp án
Xem đáp án
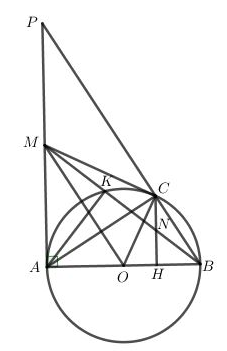
a) Ta có: (góc nội tiếp chắn nửa đường tròn);
().
Xét tứ giác AKNH có: ;
mà và ở vị trí đối nhau.
Vậy tứ giác AKNH nội tiếp trong một đường tròn.
Câu 28:
 Xem đáp án
Xem đáp án
c) Có MA, MC là hai tiếp tuyến của (O; R) cắt nhau tại M nên .
Suy ra (so le trong) (1);
(góc nội tiếp cùng chắn ) (2).
Từ (1) và (2) ta được (đpcm).
Câu 29:
 Xem đáp án
Xem đáp án
d) Gọi . Vì MO//BC nên M là trung điểm của AP.
Ta có .
Áp dụng định lý Talet ta được: .
Mà .
Vậy N là trung điểm của CH.
Câu 30:
Cho tam giác AMB cân tại M nội tiếp đường tròn(O; R). Kẻ MH vuông góc với AB . MH cắt đường tròn tại N. Biết .
1. Tính MH và bán kính R của đường tròn.
 Xem đáp án
Xem đáp án
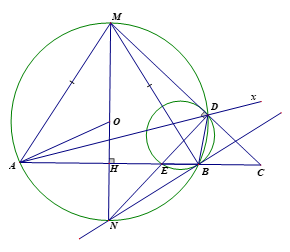
Tính MH và bán kính R của đường tròn.
Vì là tam giác cân, mà .
Xét vuông tại H.
Ta có: .
Vì nội tiếp đường tròn (O; R) .
Vì (, AB là dây cung của (O; R))
hay R+OH=8cm.
Xét vuông tại H
Ta có: .
.
Câu 31:
 Xem đáp án
Xem đáp án
· Chứng minh rằng tứ giác MDEH nội tiếp.
Ta có: ( góc nội tiếp chắn nửa đường tròn).
Xét tứ giác MDEH có:
( Hai góc đối diện bù nhau).
tứ giác MDEH nội tiếp đường tròn.
· Chứng minh rằng:.
Vì tại H mà HA=HB (chứng minh trên)
Xét và có:
là góc chung.
( hai góc và là hai góc nội tiếp đường tròn (O;R))
Mà
(g - g)
(đpcm)
· Chứng minh rằng: .
Ta có: ( hai góc và là hai góc nội tiếp đường tròn (O;R)). Mà
là tia phân giác của góc .
( tính chất tia phân giác) (1)
Mặt khác: (chứng minh trên)
mà (chứng minh trên) (đối đỉnh)
là tia phân giác ngoài của góc
( tính chất tia phân giác) (2)
Từ (1),(2) (đpcm)
Câu 32:
 Xem đáp án
Xem đáp án
3. Chứng minh NB tiếp xúc với đường tròn ngoại tiếp tam giác BDE.
Ta có: (chứng minh trên) hay .
Xét đường tròn (O') ngoại tiếp có:
là góc nội tiếp chắn cung .
là góc có đỉnh B năm trên đường tròn tạo bởi dây BE và đường BN chắn cung .
Mà (chứng minh trên).
Góc phải là góc tạo bởi tiếp tuyến và dây cung hay BN là tiếp tuyến của đường tròn
(O') Hay NB tiếp xúc với đường tròn ngoại tiếp tam giác BDE (đpcm).
Câu 33:
 Xem đáp án
Xem đáp án
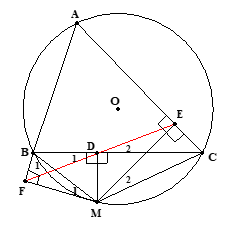
a) Bốn điểm M, B, D, F cùng thuộc một đường tròn và bốn điểm M, D, E, C cùng thuộc một đường tròn.
Ta có: nên .
nên .
Tứ giác MDBF có
Do đó tứ giác MDBF nột tiếp.
Suy ra 4 điểm M, B, D, F cùng thuộc một đường tròn.
Ta có : nên .
nên .
Suy ra: .
Mà 2 đỉnh D, F cùng nhìn MC dưới 1 góc bằng nhau.
Do đó tứ giác MDEC nột tiếp.
Vậy 4 điểm M, D, E, C cùng thuộc một đường tròn.
Câu 34:
 Xem đáp án
Xem đáp án
b) Chứng minh D, E, F thẳng hàng.
Vì tứ giác MDBF nội tiếp.
Nên: (cùng chắn ).
Vì tứ giác MDEC nội tiếp nên .
Mặt khác tứ giác MBAC nội tiếp.
Nên (góc ngoài của tứ giác nội tiếp).
Do đó (cùng phụ với ).
Suy ra: .
Mà
Nên .
Vậy D, E, F thẳng hàng.
Câu 36:
 Xem đáp án
Xem đáp án
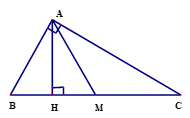
có: ,
có:
Câu 37:
b) Vẽ đường trung tuyến của tam giác ABC, tính AM và diện tích tam giác AHM
 Xem đáp án
Xem đáp án
b) có: , MB=MC (gt)
.
Câu 38:
Cho đường tròn (O) của đường kính AB. Vẽ tiếp tuyến Ax với đường tròn(O) ( A là tiếp điểm). Qua C thuộc tia Ax vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E ( D nằm giữa C và E; D và E nằm về hai phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.
a) Tứ giác AOHC nội tiếp.
 Xem đáp án
Xem đáp án
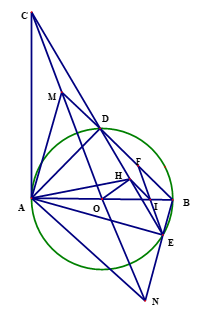
a) Ta có: ,
Tứ giác AOHC nội tiếp.
Câu 40:
 Xem đáp án
Xem đáp án
b) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F
Vì tứ giác AOHC nội tiếp
Suy ra tứ giác AHIE nội tiếp .
Mà H là trung điểm của là trung điểm của EF.
Ta có: FE//MN và IE=FI là trung điểm của đoạn thẳng MN
Tứ giác AMBN là hình bình hành .
Câu 41:
Cho tứ giác ABCD nội tiếp đường tròn tâm O, đường kính AD=2R..Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD tại F
1. Chứng minh ABEF nội tiếp.
 Xem đáp án
Xem đáp án

1. Suy ra tứ giác ABEF nội tiếp
Câu 42:
2. Chứng minh
 Xem đáp án
Xem đáp án
2. ( do tứ giác ABEF nội tiếp )
3.Ta có
Suy ra (cạnh huyền – góc nhọn)
4.Ta có
Gọi OH là đường cao của tam giác OBC
Suy ra diện tích cần tính (Phần tô đen)
(đơn vị diện tích)
Câu 43:
 Xem đáp án
Xem đáp án
3.Ta có
Suy ra (cạnh huyền – góc nhọn)
Câu 44:
4. Giả sử Tính theo R diện tích giới hạn dây BC và cung nhỏ BC.
 Xem đáp án
Xem đáp án
4.Ta có
Gọi OH là đường cao của tam giác OBC
Suy ra diện tích cần tính (Phần tô đen)
(đơn vị diện tích)
Câu 45:
 Xem đáp án
Xem đáp án
1. Ta có: (góc nội tiếp chắn nửa đường tròn)
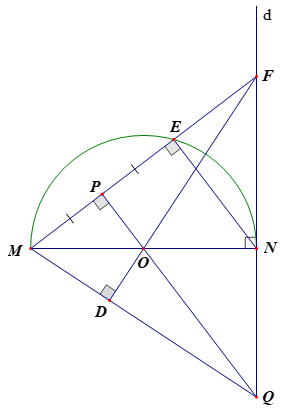
Lại có:
P là trung điểm của ME
O là trung điểm của MN
là đường trung bình của
- Xét tứ giác ONFP ta có :
(tính chất tiếp tuyến)
( do )
là tứ giác nội tiếp ( đpcm).
Câu 46:
 Xem đáp án
Xem đáp án
2. Xét ta có:
O là trực tâm
( đpcm)
- Ta có:
Mà
Nên
Từ đó suy ra (dpcm)
Câu 47:
 Xem đáp án
Xem đáp án
3. Theo BĐT Cauchy ta được:
Đẳng thức xảy ra
Mà
Nên E là trung điểm MF
Xét ta có:
là điểm chính giữa cung .
Câu 48:
 Xem đáp án
Xem đáp án
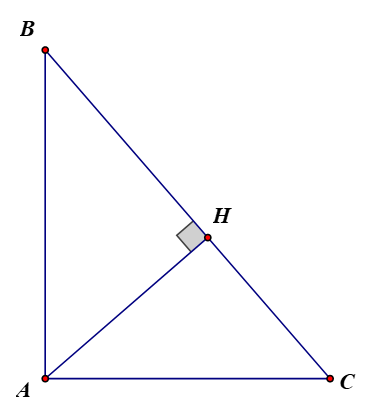
vuông tại A nên theo định lí Pi-ta-go ta có:.
.
.
(Vì độ dài BC là 1 số dương).
b).
Ta có diện tích tam giác ABC được tính như sau:.
.
Hoặc:.
.
Câu 49:
 Xem đáp án
Xem đáp án
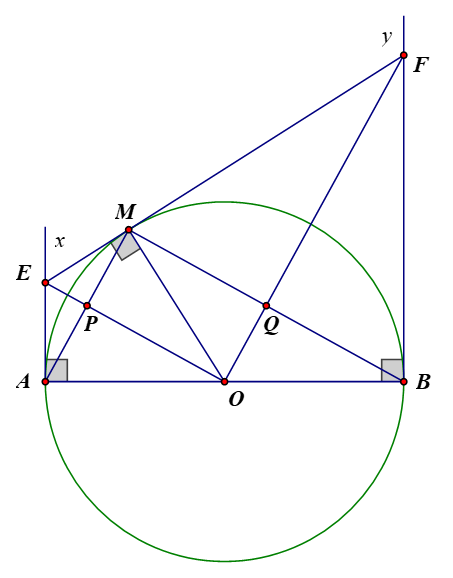
a) EM là tiếp tuyến của (O) nên
EA là tiếp tuyến của (O) nên .
Tứ giác AEMO có: mà 2 góc này ở vị trí đối nhau là tứ giác nội tiếp (dấu hiệu nhận biết).
Câu 50:
b) AM cắt OE tại P, BM cắt OF tại Q. Chứng minh tứ giác MPOQ là hình chữ nhật.
 Xem đáp án
Xem đáp án
b)
Xét và có:.
EO chung;
AO=MO;
(cạnh huyền – cạnh góc vuông).
trung trực của đoạn MA.
Mà trung trực của đoạn MA.
là trung trực của AM.
hay .
Điểm đường kính hay .
Chứng minh tương tự ta có: .
Xét tứ giác OPMQ có: .
là hình chữ nhật (dấu hiệu nhận biết).
Suy ra điều phải chứng minh.
Câu 51:
 Xem đáp án
Xem đáp án
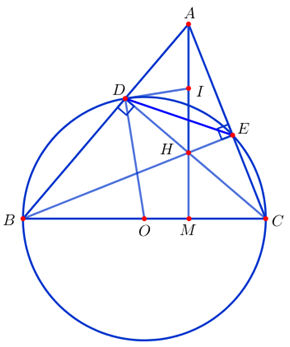
a) Xét đường tròn (O) ta có:
và là hai góc nội tiếp chắn nửa đường tròn.
.
Xét tứ giác ADHE có: mà hai góc này đối nhau nên tứ giác ADHE nội tiếp trong một đường tròn.
Ta có và cùng nội tiếp đường tròn có đường kính AH.
Nên tứ giác ADHE nội tiếp trong một đường tròn tâm I, đường kính AH hay I là trung điểm của AH.
Câu 52:
 Xem đáp án
Xem đáp án
b) Vì tứ giác ADHE nội tiếp nên (hai góc cùng nhìn đoạn HE).
Mà (hai góc nội tiếp cùng chắn cung EC trong đường tròn (O)).
Trong có , (cm ở câu a).
Mà
Nên H là trực tâm
tại M
vuông tại M.
Xét hai tam giác vuông và có:
(cmt)
(các cặp cạnh tương ứng tỉ lệ).
(đpcm).
Câu 53:
 Xem đáp án
Xem đáp án
c) Ta có: ( cân tại I, ID=IH: bán kính (I)). (1)
Mà (đối đỉnh). (2)
Từ (1) và (2) suy ra (3)
Ta lại có: ( cân tại O, OD=OC: bán kính (O)).
Hay . (4)
Xét vuông tại H có:
Từ (3) và (4) suy ra
tại
Vậy ID là tiếp tuyến của (O).
Câu 54:
d) Tính theo R diện tích của tam giác ABC, biết , và BC=2R.
 Xem đáp án
Xem đáp án
d) Ta có (cmt).
Xét tam giác vuông và có:
Mà
Diện tích tam giác ABC là:
(đvdt).
Câu 55:
 Xem đáp án
Xem đáp án
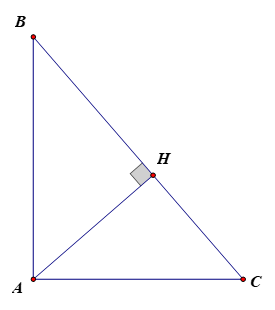
a)
vuông tại A nên theo định lí Pi-ta-go ta có:
.
(Vì độ dài BC là 1 số dương).
Câu 56:
 Xem đáp án
Xem đáp án
b)
Ta có diện tích tam giác ABC được tính như sau:
.
Hoặc:
.
Câu 57:
 Xem đáp án
Xem đáp án
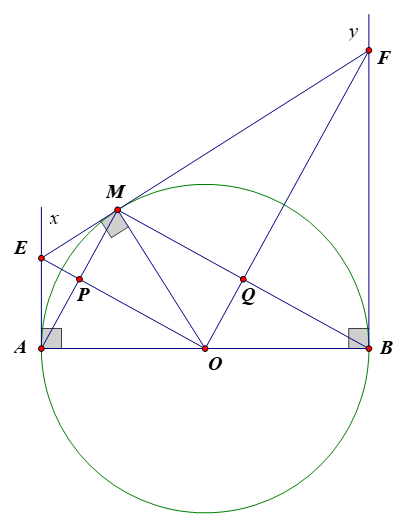
a) EM là tiếp tuyến của (O) nên
EA là tiếp tuyến của (O) nên .
Tứ giác AEMO có: mà 2 góc này ở vị trí đối nhau là tứ giác nội tiếp (dấu hiệu nhận biết)Câu 58:
 Xem đáp án
Xem đáp án
Xét và có:.
EO chung;
AO=MO;
(cạnh huyền – cạnh góc vuông).
trung trực của đoạn ![]() .
.
Mà trung trực của đoạn ![]() .
.
là trung trực của AM.
hay .
Điểm đường kính hay .
Chứng minh tương tự ta có: .
Xét tứ giác OPMQ có: .
là hình chữ nhật (dấu hiệu nhận biết).
Câu 59:
Cho đường tròn tâm O bán kính R và một đường thẳng d cố định không giao nhau. Hạ OH vuông góc với d. M là một điểm tùy ý trên d (M không trùng với H). Từ M kẻ hai tiếp tuyến MP và MQ với đường tròn (O;R) (P, Q là các tiếp điểm và tia MQ nằm giữa hai tia MH và MQ). Dây cung PQ cắt OH và OM lần lượt tại I và K.
a. Chứng minh rằng tứ giác OMHQ nội tiếp.
 Xem đáp án
Xem đáp án
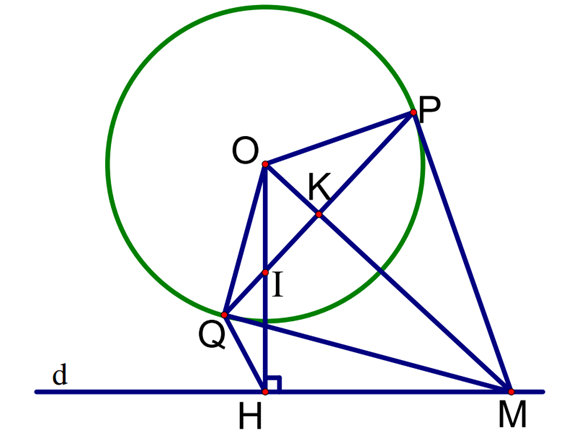
1. Chứng minh rằng tứ giác OMHQ nội tiếp.
; (MQ là tiếp tuyến của (O) tại Q).
Vậy tứ giác OMHQ nội tiếp.
Câu 60:
2. Chứng minh rắng
 Xem đáp án
Xem đáp án
2) Chứng minh rằng .
OP=OQ=R; MP=MQ (MP; MQ là hai tiếp tuyến của (O))
là trung trực của PQ.
.
Do đó: và (đpcm).
Câu 61:
 Xem đáp án
Xem đáp án
3) Chứng minh rằng khi điểm M di chuyển trên đường thẳng d thì điểm I luôn cố định.
Xét và có: (cmt) và
đồng dạng với (g-g)
(1).
Mặt khác: vuông tại P có . (2)
Từ (1) và (2) suy ra (không đổi).
Mà O và d cố định nên OH không đổi không đổi. Vậy điểm I luôn cố định .
Câu 62:
4. Biết , tính IP.IQ
 Xem đáp án
Xem đáp án
4. Biết , tính IP.IQ.
Ta có: .
.
Lại có: (theo gt).
và H cùng thuộc đường tròn đường kính OM.
Xét và có: (đối đỉnh) và (góc nội tiếp cùng chắnc ung OQ).
đồng dạng với (g-g)
Câu 63:
Cho tam giác ABC (AB<AC) có ba góc nhọn nội tiếp đường tròn (O) và D là hình chiếu vuông góc của B trên AO sao cho D nằm giữa A và D. Gọi M là trung điểm của BC, N là giao điểm của BD và AC, F là giao điểm của MD và AC, E là giao điểm thứ hai của BD với đường tròn (O). H là giao điểm của BF và AD. Chứng minh rằng:
a) Tứ giác BDOM nội tiếp và . Xem đáp án
Xem đáp án
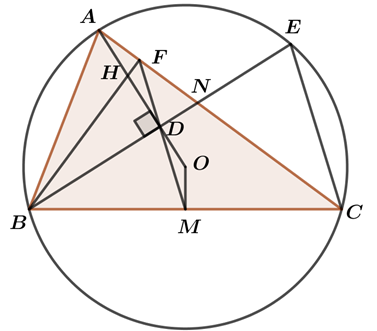
a)
M là trung điểm BD suy ra
Tứ giác BDOM có
suy ra tứ giác BDOM nội tiếp.
Vì tứ giác BDOM nội tiếp
suy ra
Mà (góc nội tiếp cùng chắn cung ).
Câu 64:
 Xem đáp án
Xem đáp án
b) Ta có
(đđ)
Suy ra
Mặt khác: (góc nội tiếp cùng chắn cung )
Vậy
Vì DF//EC nên (đpcm)
Câu 65:
c) CA là tia phân giác góc
 Xem đáp án
Xem đáp án
c) Vì DF//EC suy ra , mà
Suy ra hay tứ giác ABDF nội tiếp
Suy ra vuông tại F có FM là đường trung tuyến nên FM=MC suy ra cân tại hayCâu 66:
 Xem đáp án
Xem đáp án
d) Tam giác ANB có AD và BF là hai đường cao cắt nhau tại H nên H là trực tâm của tam giác NAB hay
Câu 67:
Một cốc nước có dạng hình trụ có bán kính đáy bằng 3cm, chiều cao bằng 12cm và chứa một lượng nước cao 10cm. Người ta thả từ từ 3 viên bi làm bằng thủy tinh có cùng đường kính bằng 2cm vào cốc nước. Hỏi mực nước trong cốc lúc này cao bao nhiêu?
 Xem đáp án
Xem đáp án
Thể tích của ba viên bi:
Thể tích của mực nước dâng lên bằng đúng thể tích của 3 viên bi, do đó nếu gọi là thể tích của mực nước dâng lên và h là độ cao của mực nước dâng lên thêm
Ta có:
Vậy mực nước trong cốc lúc này là:
Do đó, nước chưa tràn ra khỏi cốc và mực nước trong cốc lúc này là .
Câu 68:
Cho nửa đường tròn tâm O đường kính AB=2R. Gọi M là điểm chính giữa của cung AB, N là điểm bất kỳ thuộc cung MB (N khác M và B). Tia AM và AN cắt tiếp tuyến tại B của nửa đường tròn tâm O lần lượt tại C và D
1. Tính số đo .
 Xem đáp án
Xem đáp án
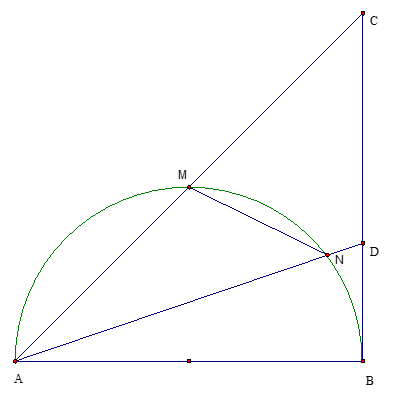
1. Tính số đo .
Vì M là điểm chính giữa cung AB nên là góc nội tiếp chắn nửa đường tròn. Suy ra tam giác AMB vuông cân tại M. Từ đó:
Tam giác ABC vuông tại B có nên là tam giác vuông cân tại B Suy ra
Câu 69:
 Xem đáp án
Xem đáp án
2. Chứng minh tứ giác MNDC nội tiếp trong một đường tròn.
Ta có: (góc nội tiếp chắn cung AM bằng đường tròn)
Lại có: (vì )
Tứ giác MNDC có nên nội tiếp được đường tròn (góc trong bằng góc ngoài tại đỉnh đối diện)
Câu 70:
4. Chứng minh
 Xem đáp án
Xem đáp án
3. Chứng minh
Ta có: (1); (góc nội tiếp chắn ![]() đường tròn);
đường tròn);
(câu 2). Nên (2)
Từ (1) và (2) suy ra ∽(g-g). Suy ra:
Tam giác ABC vuông tại B có BM là đường cao cho:
Vậy:
Câu 71:
Cho hình nón có đường sinh bằng 26cm diện tích xung quanh là Tính bán kính đáy và thể tích của hình nón.
 Xem đáp án
Xem đáp án

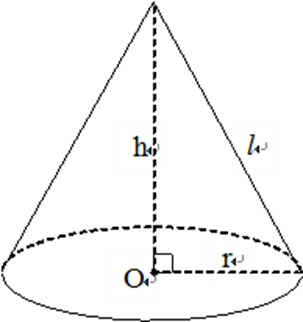
Ta có:
Câu 72:
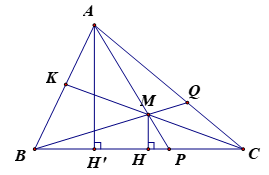
Cho tam giác ABC nhọn có ba đường cao AD, BE, CF cắt nhau tại điểm H. Gọi M là trung điểm của đoạn AH.
1) Chứng minh tứ giác AEHF nội tiếp đường tròn.
 Xem đáp án
Xem đáp án
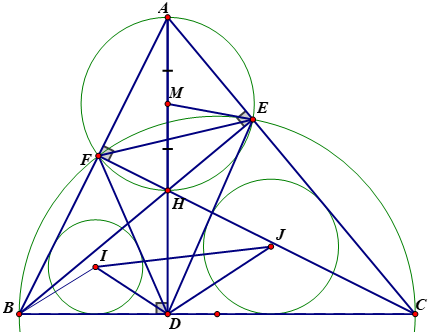
1) Chứng minh tứ giác AEHF nội tiếp được đường tròn
Trong tứ giác AEHF có: (vì BE ^ AC và CF ^ AB)
Vậy mà hai góc này ở vị trí đối nhau nên tứ giác AEHF nội tiếp được đường tròn
Câu 73:
 Xem đáp án
Xem đáp án
2) Chứng minh CE.CA = CD.CB
Xét ∆CAD vuông tại D và ∆CBE vuông tại E có: góc C chung
Vậy ∆CAD ∆CBE ÞCâu 74:
 Xem đáp án
Xem đáp án
3) Chứng minh EM là tiếp tuyến của đường tròn ngoại tiếp ∆BEF
Trong tứ giác BFEC có: (vì BE ^ AC và CF ^ AB)
mà hai góc này cùng chắn cạnh BC nên tứ giác BFEC nội tiếp đường tròn đường kính BC.
Hay ∆BEF nội tiếp đường tròn đường kính BC.
Vì M là trung điểm của cạnh huyền AH trong tam giác vuông AEH nên ME = MH Þ ∆MEH cân tại M
Þ hay mà phụ (∆AHE vuông tại E)
Þ phụ hay phụ
Mặt khác phụ (∆ADC vuông tại D) hay phụ
Vậy (cùng phụ )
Trong đường tròn ngoại tiếp ∆BEF có Þ ME là tiếp tuyến tại E của đường tròn này (vì có góc tạo bởi tia tiếp tuyến và góc nội tiếp cùng chắn cung EB)
Cách 2: Gọi O là trung điểm của BC. Chứng minh ME ^ EO
Trong tứ giác BFEC có: (vì BE ^ AC và CF ^ AB) mà hai góc này cùng chắn cạnh BC nên tứ giác BFEC nội tiếp đường tròn có tâm O là trung điểm BC.
Hay ∆BEF nội tiếp đường tròn tâm O.
Vì M là trung điểm của cạnh huyền AH trong tam giác vuông AEH nên ME = MH Þ ∆MEH cân tại M
Þ mà nên (1)
Tương tự:
Lại có O là trung điểm của cạnh huyền BC trong tam giác vuông BEC nên OE = OB
Þ ∆OBE cân tại O
Þ hay (2)
Từ (1) và (2) ta có:
(vì ∆HBD vuông tại D)
Þ ME ^ OE mà E thuộc đường tròn (O) ngoại tiếp ∆BEF
Þ ME là tiếp tuyến của đường tròn ngoạiCâu 75:
4) Gọi I và J lần lượt là tâm đường tròn nội tiếp hai tam giác BDF và EDC. Chứng minh .
 Xem đáp án
Xem đáp án

Xét ∆ECD và ∆BCA có:
Góc C chung
(vì )
Vậy ∆ECD ∆BCA (cạnh – góc – cạnh)
Chứng minh tương tự ta có: ∆BFD ∆BCA
Vậy ∆ECD ∆BFD (tính chất bắc cầu) Þ (3);
Xét ∆BID và ∆EJD có
(vì )
(vì )
Vậy ∆BID ∆EJD (góc – góc) Þ (4)
Từ (3) và (4) Þ
Dễ chứng minh: (cùng bù góc FDB)
Xét ∆DCF và ∆DJI có:
(vì)
Vậy ∆DCF ∆DJI (cạnh – góc – cạnh) Þ (hai góc tương ứng)
Câu 76:
Cho đường tròn (O) có AB là một dây cung cố định không đi qua O. Từ một điểm M bất kì trên cung lớn AB (M không trùng A và B) kẻ dây cung MN vuông góc với AB tại H. Gọi MQ là đường cao của tam giác AMN (Q thuộc AN).
a) Chứng minh tứ giác AMHQ nội tiếp đường tròn.
 Xem đáp án
Xem đáp án

Theo đề bài, ta có (Cùng bằng 90o).
Tứ giác AMHQ nội tiếp (Bài toán quỹ tích cung chứa góc).
Câu 77:
b) Gọi I là giao điểm của AB và MQ. Chứng minh tam giác IBM cân
 Xem đáp án
Xem đáp án
b) Theo ý a) thì tứ giác AMHQ nội tiếp
(Hai góc nội tiếp cùng chắn một cung thì bằng nhau).
Tứ giác AMBN nội tiếp (Hai góc nội tiếp cùng chắn một cung thì bằng nhau)
(Cùng bằng ).
Mà MH ở giữa MI và MB là phân giác của .
Tam giác MIB có MH vừa là đường cao, vừa là phân giác nên cân tại M.
Vậy tam giác IBM cân.
Câu 78:
c) Kẻ MP vuông góc với BN tại P. Xác định vị trí của M sao cho MQ.AN+MP.BN đạt giá trị lớn nhất.
 Xem đáp án
Xem đáp án
c) Ta có .
Mà (Trong các dây của một đường tròn, dây lớn nhất là đường kính)
(không đổi).
Dấu "=" xảy ra là điểm chính giữa của cung lớn AB.
Vậy lớn nhất bằng 2.AB.R, đạt được khi M là điểm chính giữa của cung lớn ABCâu 79:
Cho đường tròn (O), từ một điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB của đường tròn (A, B là hai tiếp điểm). Kẻ đường kính BE của đường tròn (O). Gọi F là giao điểm thứ hai của đường thẳng ME và đường tròn (O). Đường thẳng AF cắt MO tại điểm N. Gọi H là giao điểm của MO và AB.
1. Chứng minh tứ giác MAOB nội tiếp đường tròn.
 Xem đáp án
Xem đáp án
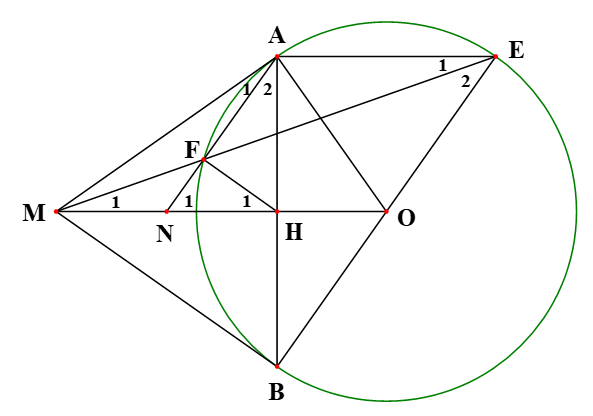
1. Ta có Mà hai góc đối nhau nên tứ giác MAOB nội tiếp.
Câu 80:
2. Chứng minh AE//MO
 Xem đáp án
Xem đáp án
2. Ta có tam giác AOE cân tại O nên . (1)
Ta lại có (2)
Từ (1) và (2) suy raCâu 81:
3. Chứng minh
 Xem đáp án
Xem đáp án
3. Xét hao tam giác và có:
và (góc so le trong, góc tạo bởi tia tiếp tuyến và dây dung)
(g.g)
Câu 82:
 Xem đáp án
Xem đáp án
4. Ta có MA=MB (tính chất 2 tiếp tuyến cắt nhau) và OA=OB=R
là đường trung trực của AB
và HA=HB
và có:
chung
(g.g)
.
Áp dụng hệ thức lượng vào tam giác vuông MAO, ta có .
Do đó
(c.g.c)
Vì là góc vuông nội tiếp (O) nên E, O, B thẳng hàng
Áp dụng hệ thức lượng vào tam giác vuông NHA ta có
Câu 83:
Cho đường tròn tâm O, đường kính AB cố định. H là điểm cố định thuộc đoạn OA(H không trùng O và A). Qua H vẽ đường thẳng vuông góc với AB cắt đường tròn tâm O tại C và D. Gọi K là điểm tùy ý thuộc cung lớn CD (K không trùng các điểm C, D và B). Gọi I là giao điểm của AK và CD.
a) Chứng minh tứ giác HIKB nội tiếp đường tròn.
 Xem đáp án
Xem đáp án
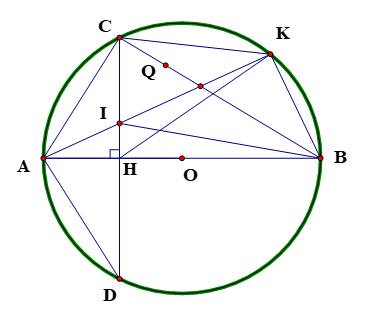
a) Tứ giác HIKB có (gt).
(góc nội tiếp chắn nửa đường tròn) suy ra tứ giác HIKB nội tiếp đường tròn (đpcm).
Câu 84:
 Xem đáp án
Xem đáp án
b) Xét có góc A chung, có (cùng chắn cung HI của đường tròn ngoại tiếp tứ giác HIKB).
Suy ra đồng dạng với .
Suy ra (đpcm).
Câu 85:
 Xem đáp án
Xem đáp án
c) Đường kính AB vuông góc với dây CD tại H (gt) , suy ra
Suy ra .
Suy ra (cùng chắn hai cung bằng nhau).
Mặt khác tia CA và điểm K nằm trên hai nửa mặt phẳng đối nhau bờ là đường thẳng CI.
Suy ra CA là tiếp tuyến của đường tròn ngoại tiếp tam giác KCI tại tiếp điểm C.
(H/s có thể chứng minh để suy ra CA là tiếp tuyến).
Gọi Q là tâm đường tròn ngoại tiếp tam giác KCI, suy ra Q nằm trên đường thẳng vuông góc với CA tại C.
Mặt khác (góc nội tiếp chắn nửa đường tròn) , suy ra Q thuộc đường thẳng CB cố định (đpcm).
Câu 86:
Cho đường tròn tâm O, bán kính R. Từ một điểm M ở ngoài đường tròn, kẻ hai tiếp tuyến MA và MB với đường tròn (A, B là các tiếp điểm). Qua A, kẻ đường thẳng song song với MO cắt đường tròn tại E (E khác A), đường thẳng ME cắt đường tròn tại F(F khác E), đường thẳng AF cắt MO tại N, H là giao điểm của MO và AB.
1. Chứng minh: Tứ giác MAOB nội tiếp đường tròn.
 Xem đáp án
Xem đáp án
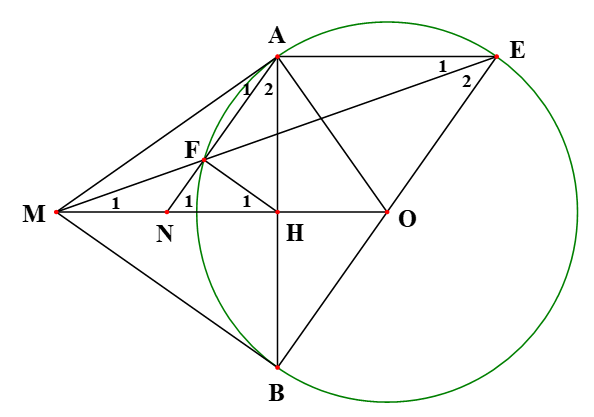
1) Vì MA, MB là các tiếp tuyến của (O) nên .
Tứ giác MAOB có
Tứ giác MAOB nội tiếp đường tròn.
Câu 87:
2. Chứng minh: và MN=NH
 Xem đáp án
Xem đáp án
2. * Ta có: (so le trong, AE//MO) và (cùng bằng sđ)
.
Xét và có: chung;
.
* Có MA=MB (tính chất 2 tiếp tuyến cắt nhau) và OA=OB=R
là đường trung trực của AB
AH MO và HA = HB.
Xét và có: chung;
.
Áp dụng hệ thức lượng vào vuông MAO có: .
Do đó:
.
Vì là góc vuông nội tiếp (O) nên E,O,B thẳng hàng.
(vì =sđ)
.
Áp dụng hệ thức lượng vào vuông NHA có:
.
Câu 88:
3. Chứng minh:
 Xem đáp án
Xem đáp án
3) Chứng minh: .
Áp dụng hệ thức lượng vào vuông NHA có: và
Mà .
Vì AE//MN nên (hệ quả của định lí Ta-lét)
.
Câu 89:
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.
1) Chứng minh bốn điểm C, N, K, I cùng thuộc một đường tròn.
 Xem đáp án
Xem đáp án
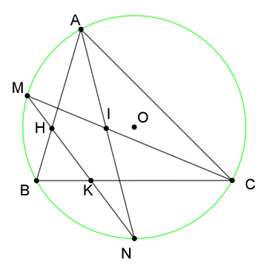
a) Chứng minh bốn điểm C, N, K, I cùng thuộc một đường tròn.
Vì M là điểm chính giữa cung nhỏ AB của (O) (giả thiết)
(hai góc nội tiếp chắn hai cung bằng nhau)
Xét tứ giác CNKI ta có:
(vì )
là tứ giác nội tiếp (tứ giác có 2 đỉnh kề nhau cùng nhìn một cạnh dưới hai góc bằng nhau)
N, K, I cùng thuộc một đường tròn.
Câu 90:
2. Chứng minh
 Xem đáp án
Xem đáp án
Vì N là điểm chính giữa cung nhỏ BC của (O) (giả thiết)
(hai góc nội tiếp chắn hai cung bằng nhau).
Xét và ta có:
- là góc chung.
- (vì )
.
Câu 91:
3. Chứng minh tứ giác BHIK là hình thoi.
 Xem đáp án
Xem đáp án
+ Chứng minh BIHK là hình bình hành.
Gọi J là giao điểm của AN và BC.
Ta có: (cmt)
(hai góc nội tiếp chắn hai cung bằng nhau)
là phân giác của
là phân giác trong của
(1)
Ta có: (cmt)
(hai góc nội tiếp chắn hai cung bằng nhau)
là phân giác của .
là phân giác trong của
(2)
Ta có:
(hai góc nội tiếp chắn hai cung bằng nhau).
Xét và ta có:
- (hai góc nội tiếp cùng chắn )
- (cmt)
(3)
Từ (1), (2), (3) suy ra
(định lí Thales đảo) hay (4)
Chứng mình tương tự các ý ở trên, ta được KI//BH (5)
Từ (4) và (5) suy ra BHIK là hình bình hành.
+ Chứng minh BH=BK.
Ta có : (cmt) (6)
Chứng minh tương tự câu b) ta có:
(7)
Từ (6) và (7) suy ra BH=BK
Mà BHIK là hình bình hành nên BHIK là hình thoi.
Câu 92:
 Xem đáp án
Xem đáp án
d) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ . Vẽ đường kính ND của đường tròn (O). Chứng minh ba điểm D, E, K thẳng hàng.
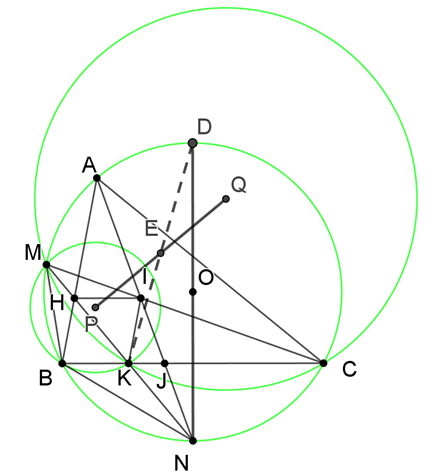
Ta có:
(cmt)
là tiếp tuyến tại B của (P)
Mà (vì : góc nội tiếp chắn nửa đường tròn tâm O)
nên B, P, D thằng hàng.
Ta có: cân tại P (PB=PK)
(8)
Ta có: là đường trung trực của đoạn BC
(D thuộc đường thẳng ON)
cân tại D
(9)
Từ (8) và (9) suy ra
Mà hai góc này ở vị trí đồng vị nên (10)
Chứng minh tương tự ta có: C, Q, D thẳng hàng và (11)
Từ (10) và (11) suy ra DPKQ là hình bình hành
Mà E là trung điểm của đường chéo PQ nên E cũng là trung điểm của đường chéo DK
thẳng hàng.
Câu 93:
Cho đường tròn tâm O, bán kính R, đường kính BC. Gọi A là một điểm thuộc đường tròn (A khác B và C). Đường phân giác cắt BC tại D và cắt đường tròn tại M
1. Chứng minh MB=MC và OM vuông góc với BC.
 Xem đáp án
Xem đáp án
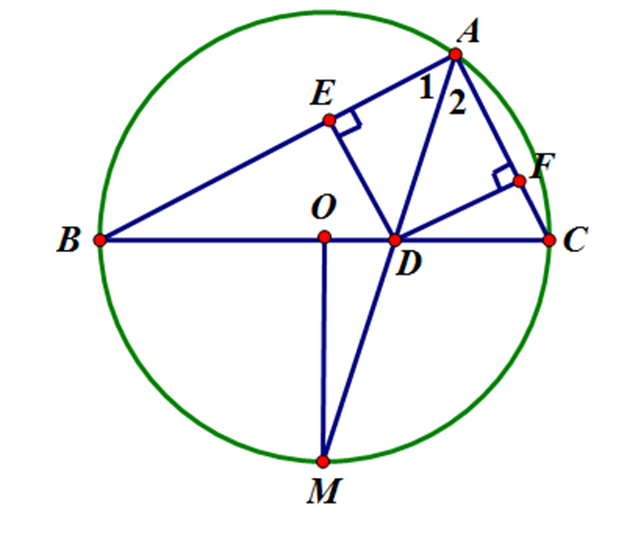
1. Vì AD là tia phân giác của góc nên BM=CM.
Vì OB = OC và MB = MC nên OM là đường trung trực của BC nên
Câu 94:
 Xem đáp án
Xem đáp án
3. Ta có suy ra cung AC có số đo bằng 1200 và cung AB có số đo bằng 600, suy ra AB = R
Và
Áp dụng tính chất đường phân giác ta có
Suy ra
Do đó
Diện tích tam giác DMC là: .Câu 95:
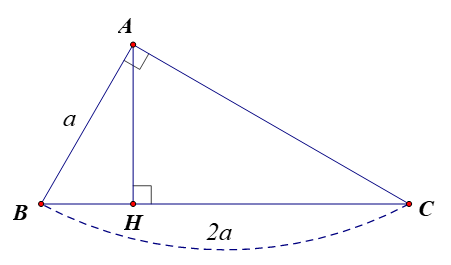
1. Cho tam giác ABC vuông tại A có AB=30 cm, AC=40 cm. Tính độ dài đường cao AH và số đo góc B (làm tròn đến độ).
 Xem đáp án
Xem đáp án
1.Ta có
Câu 96:
2. Từ điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB, AC với đường tròn (O), (B, C là hai tiếp điểm).
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.
 Xem đáp án
Xem đáp án

Vẽ hình đúng đến câu a)
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.
suy ra tứ giác ABOC nội tiếp được đường tròn.
Câu 97:
b) Vẽ cát tuyến ADE của (O) sao cho cát tuyến ADE nằm giữa 2 tia AO, AB; D, E thuộc đường tròn (O) và D nằm giữa A, E. Chứng minh .
 Xem đáp án
Xem đáp án
b) Vẽ cát tuyến ADE của (O) sao cho cát tuyến ADE nằm giữa 2 tia AO, AB; D, E thuộc đường tròn (O) và D nằm giữa A, E. Chứng minh .
Tam giác ADB đồng dạng với tam giác ABE
Câu 98:
 Xem đáp án
Xem đáp án
c) Gọi F là điểm đối xứng của D qua AO, H là giao điểm của AO và BC. Chứng minh: ba điểm E, F, H thẳng hàng.
Hai tam giác ADH và AOE đồng dạng suy ra
Tam giác DOE cân tại O suy ra
Tứ giác DHOE nội tiếp suy ra
suy ra
nên . Suy ra ba điểm E, F, H thẳng hàng.
Câu 99:
1. Từ điểm M nằm bên ngoài đường tròn (O; R) vẽ các tiếp tuyến MA, MB (A, B là các tiếp điểm).
a) Chứng minh rằng bốn điểm M, A, O, B cùng nằm trên một đường tròn;
 Xem đáp án
Xem đáp án
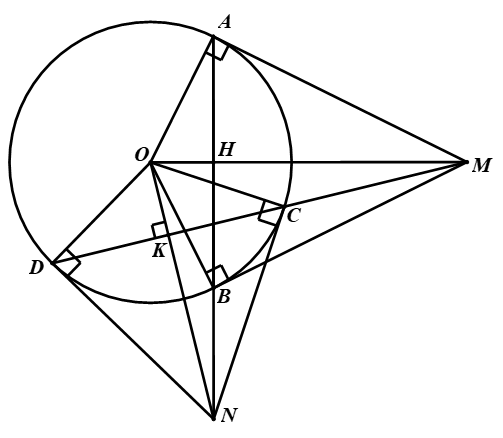
+ Xét đường tròn (O) có MA, MB là tiếp tuyến
+ Xét tứ giác MAOB có
Mà hai góc này ở vị trí đối nhau
Suy ra tứ giác MAOB nội tiếp đường tròn.
Do đó bốn điểm M, A, O, B cùng nằm trên một đường tròn.
Câu 100:
b) Vẽ cát tuyến MCD không đi qua tâm O của đường tròn đó sao cho điểm C nằm giữa hai điểm M và D. Tiếp tuyến tại điểm C và điểm D của đường tròn (O) cắt nhau tại điểm N. Gọi H là giao điểm của AB và MO, K là giao điểm của CD và QN. Chứng minh rằng
 Xem đáp án
Xem đáp án
b) Ta có MA=MB (tính chất hai tiếp tuyến cắt nhau);
Lại có là đường trung trực của đoạn thẳng AB
tại H.
Xét vuông tại A, đường cao AH:
Theo hệ thức về cạnh góc vuông và đường cao trong tam giác vuông ta có:
Chứng minh tương tự ta được : (2);
Từ (1) và (2) suy ra (đpcm).
Câu 101:
 Xem đáp án
Xem đáp án
Từ câu b) ta có :
Xét có:
tại H (3);
Mặt khác tại H (4);
+ Từ (3) và (4) suy ra ba điểm A, B, N thẳng hàng (đpcm).
Câu 102:
2. Hình trụ có đường kính đáy bằng 4cm và chiều cao bằng đường kính đáy. Tính thể tích hình trụ (lấy ).
 Xem đáp án
Xem đáp án
Theo bài ra ta có: .
Áp dụng công thức tính thể tích hình trụ, ta có:
.Câu 103:
Cho đường tròn (O) có đường kính AB và điểm C thuộc đường tròn đó (C khác A, B). Lấy điểm D thuộc dây BC (D khác B, C). Tia AD cắt cung nhỏ BC tại điểm E, tia AC cắt tia BE tại điểm F.
a) Chứng minh rằng: Tứ giác FCDE là tứ giác nội tiếp đường tròn.
 Xem đáp án
Xem đáp án

a) Ta có hai góc (hai góc nội tiếp chắn nửa đường tròn).
Xét tứ giác FCDE có
Suy ra tứ giác FCDE nội tiếp đường tròn đường kính DF.
Câu 104:
 Xem đáp án
Xem đáp án
b) Xét hai tam giác vuông CDA và EDB có
(hai góc đối đỉnh).
Suy ra hai tam giác và đồng dạng.
Câu 105:
 Xem đáp án
Xem đáp án
c) Gọi I là trung điểm của DF
Vì vuông tại C có I là trung điểm của DF nên IC=IF
Suy ra cân tại (1)
Vì tứ giác FCDE nội tiếp nên (hai góc nội tiếp cùng chắn cung DC) (2)
Lại có (hai góc nội tiếp cùng chắn cung AC của (O)) và (do cân tại O) (3)
Từ (1), (2) và
Mà
Do đó
Vậy IC là tiếp tuyến của đường tròn tâm ![]()
Câu 106:
Lúc 6h sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (như hình vẽ bên dưới). Cho biết đoạn thẳng AB dài 762m, góc A bằng 6o và góc B bằng 4o.

a) Tính chiều cao h của con dốc
 Xem đáp án
Xem đáp án
a) Xét các tam giác AHC và BHC vuông tại H, ta có :
Suy ra: .
Câu 107:
b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4km/h và tốc độ trung bình xuống dốc là 19km/h.
 Xem đáp án
Xem đáp án
b) Ta có:
Gọi (giờ) lần lượt là khoảng thời gian An đi từ A đến B, A đến C và C đến B.
Khi đó: phút.
Vậy An đến trường vào lúc 6 giờ 6 phút.
Câu 108:
Cho tam giác ABC vuông tại A. Đường tròn tâm O đường kính AB cắt các đoạn BC và OC lần lượt tại D và I gọi H là hình chiếu vuông góc của A lên OC; AH cắt BC tại M.
a) Chứng minh: Tứ giác ACDH là nội tiếp và .
 Xem đáp án
Xem đáp án

a) Ta có ().
( góc nội tiếp chắn nửa đường tròn đường kính AB).
Vậy nội tiếp đường tròn đường kính AC.
( góc nội tiếp cùng chắn cung CD).
Mặt khác sđ.
( góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung ).
Từ (1); (2).
Câu 109:
 Xem đáp án
Xem đáp án
b) Ta có ( g-g) vậy .
Mà OA=OB vì AB đường kính đường tròn tâm (O). Vậy .
Xét và có:
( chung góc )
( c-g-c).
Ta có: ( hai góc nội tiếp cùng chắn cung CD của đường tròn ngoại tiếp tứ giác ACDH).
(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung của đường tròn tâm O).
Mặt khác .
Vậy mà ().
là đường phân giác của góc .
Câu 110:
 Xem đáp án
Xem đáp án
c) Xét tam giác BHD:
Vì HM là phân giác của .
Mặt khác là đường phân giác ngoài tam giác BHD.
Từ (*) và (**).
Gọi Q là giao điểm của AM với (O) vì là tiếp tuyến của của .
Vậy năm điểm C; O; A; K; Q nội tiếp một đường tròn đường kính CO.
Bốn điêm B; A; D; Q cùng thuộc .
Năm điểm C; Q; A; K; Q cùng thuộc một đường tròn .
Từ (3) và
Câu 111:
d) Gọi E là giao điểm của AM và OK; J là giao điểm của IM và (O) (J khác I ).
Chứng Minh: Hai đường thẳng OC và EI cắt nhau tại một điểm trên (O).
 Xem đáp án
Xem đáp án
d) Gọi N là giao điểm của CO và .
Mà ta có: (chứng minh trên ).
Vậy nội tiếp.
Từ (5) và thẳng hàng.
Câu 112:
Cho đường tròn (O) có tâm là điểm O, đường kính AB=2R. Trên đường thẳng lấy AB lấy H sao cho B nằm giữa A và H (H không trùng với B), qua H dựng đường thẳng d vuông góc với AB Lấy điểm C cố định thuộc đoạn thẳng OB (C không trùng với O và B). Qua điểm C kẻ đường thẳng a bất kỳ cắt đường tròn (O) tại hai điểm E, F (a không trùng với AB). Các tia AE và AF cắt đường thẳng d lần lượt tại M và N
a) Chứng minh rằng tứ giác BEMH nội tiếp đường tròn.
 Xem đáp án
Xem đáp án
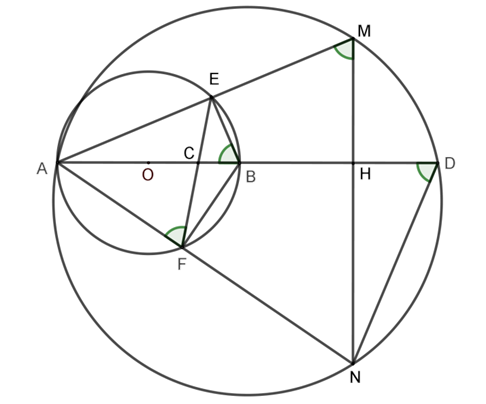
a) Ta có: (góc nội tiếp chắn nửa đường tròn)
(kề bù với ).
Tứ giác BEMH có:
Tứ giác BEHM nội tiếp.
Câu 113:
b) Chứng minh rằng tam giác AFB đồng dạng với tam giác AHN và đường tròn ngoại tiếp tam giác AMN luôn đi qua một điểm cố định khác A khi đường thẳng a thay đổi.
 Xem đáp án
Xem đáp án
b) Ta có: (góc nội tiếp chắn nửa đường tròn)
Xét và có: chung,
(g.g).
Gọi D là giao điểm thứ hai của AB với đường tròn
ngoại tiếp tam giác AMN
(2 góc nội tiếp cùng chắn cung )
Vì (2 góc nội tiếp cùng chắn cung )
và (vì tứ giác BEMH nội tiếp)
nên
Xét và có chung, (cmt)
(g.g)
Mặt khác, ta có (g.g)
Do đó,không đổi (vì A, B, C, H cố định)
Câu 114:
 Xem đáp án
Xem đáp án
c) Với AB=1 cm, BC=BH=1 cm thì:
(cm)
(cm)
Dễ thấy tam giác AHM và NHD đồng dạng (g.g)
Áp dụng bất đẳng thức Cô-si , ta có:
()
Dấu bằng xảy ra:
Vậy min
Câu 115:
Cho tứ giác ABCD nội tiếp đường tròn đường kính AB. Hai đường chéo AC và BD cắt nhau tại E, F là hình chiếu vuông góc của E trên AB.
1. Chứng minh tứ giác ADEF nội tiếp.
 Xem đáp án
Xem đáp án
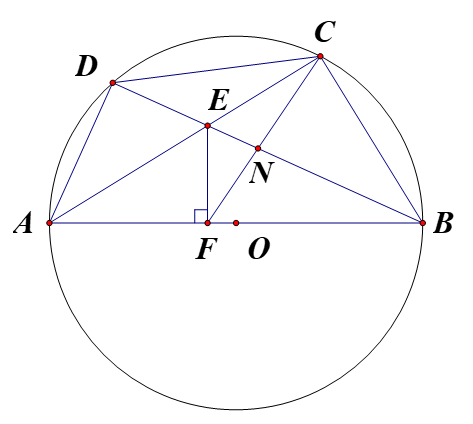
Ta có (góc nội tiếp chắn nửa đường tròn).
Xét tứ giác ADEFcó: .
Suy ra tứ giác ADEF nội tiếp đường tròn.
Câu 116:
 Xem đáp án
Xem đáp án
Chứng minh tương tự ta có tứ giác BCEF nội tiếp đường tròn.
(hai góc nội tiếp cùng chắn ). (1)
Vì tứ giác ABCD nội tiếp đường tròn (gt)
(hai góc nội tiếp cùng chắn ). (2)
Từ (1) và (2) suy ra .
Hay CA là phân giác của . (3)
Mặt khác: , hay . (4)
Từ (3) và (4) suy ra CB là phân giác ngoài của .
Áp dụng tính chất đường phân giác của tam giác cho tam giác DCN ta có
. (đpcm)
Câu 117:
Cho đường tròn (O;OA). Trên bán kính OA lấy điểm I sao cho . Vẽ dây BC vuông góc với OA tại điểm I và vẽ đường kính BD. Gọi E là giao điểm của AD và BC.
a) Chứng minh DA là tia phân giác của .
 Xem đáp án
Xem đáp án
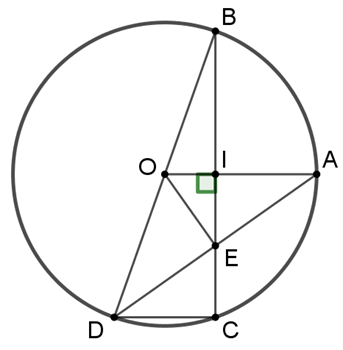
a) Chứng minh DA là tia phân giác của .
(O) có: tại I (gt)
là trung điểm của BC.
Vậy OA là trung trực của BC.
.
.
Mà và là góc nội tiếp (O) chắn và
nên .
là tia phân giác của .
Câu 118:
 Xem đáp án
Xem đáp án
b) Chứng minh OE vuông góc với AD.
Có: .
có: O, I là trung điểm của BD, BC.
là đường trung bình.
và DC=2IO.
Mà IA=2IO nên DC=IA.
Có: và nên .
Xét và có:
(g-c-g)
.
là trung điểm của AD.
(quan hệ đường kính – dây cung).
Câu 119:
c) Lấy điểm M trên đoạn AB (M khác I và B). Tia AM cắt đường tròn (O) tại điểm N. Tứ giác MNDE có phải là một tứ giác nội tiếp hay không? Vì sao?
 Xem đáp án
Xem đáp án
 c) Lấy điểm M trên đoạn IB (M khác I và B). Tia AM cắt đường tròn (O) tại điểm N. Tứ giác MNDE có phải là một tứ giác nội tiếp hay không? Vì sao?
c) Lấy điểm M trên đoạn IB (M khác I và B). Tia AM cắt đường tròn (O) tại điểm N. Tứ giác MNDE có phải là một tứ giác nội tiếp hay không? Vì sao?
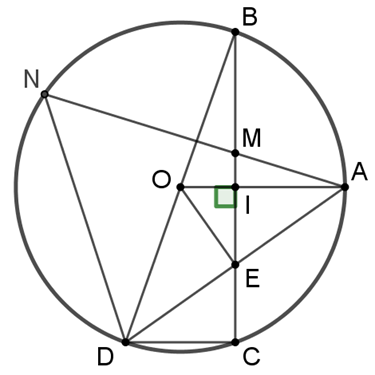
(O) có: là góc có đỉnh bên trong đường tròn.
Mà (cmt) nên .
Mặt khác (góc nội tiếp (O)) nên .
là tứ giác nội tiếp (tứ giác có góc ngoài bằng góc
trong đối diện).
Câu 120:
Tính diện tích xung quanh, diện tích toàn phần và thể tích của một hình trụ có chu vi hình tròn đáy là 16 cm và chiều cao là 5 cm.
 Xem đáp án
Xem đáp án
Bán kính hình tròn đáy là: (cm).
Diện tích xung quanh hình trụ là: (cm2).
Diện tích toàn phần hình trụ là: (cm2)
Thể tích hình trụ là: (cm3).
Câu 121:
Cho hình vuông ABCD, điểm E thuộc cạnh BC. Qua B kẻ đường thẳng vuông góc với DE, đường thẳng này cắt các đường thẳng DE và DC lần lượt tại H và K
a) Chứng minh tứ giác BHCD nội tiếp đường tròn.
 Xem đáp án
Xem đáp án
a) Điểm H và C cùng nhìn đoạn BC dưới một góc 90o
Suy ra tứ giác BHCD nội tiếp đường tròn đường kính BD
Câu 122:
 Xem đáp án
Xem đáp án
b) Do tứ giác BHCD nội tiếp, suy ra
 và là góc bẹt nên
và là góc bẹt nên
Từ (1) và (2) suy ra
Xét và có và chung.
Suy ra
Câu 123:
c) Giả sử hình vuông ABCD có cạnh là 3cm. Tính độ dài cung CH có số đo bằng 40o của đường tròn đường kính BD (làm tròn kết quả đến một chữ số thập phân).
 Xem đáp án
Xem đáp án
c) Giả sử hình vuông ABCD có cạnh là 3cm
Tính độ dài cung CH có số đo bằng 40o của đường tròn
đường kính BD (làm tròn kết quả đến một chữ số thập phân).
Do hình vuông ABCD có cạnh bằng 3cm nên
Do đó bán kính đường tròn ngoại tiếp tứ giác BHCD là
Độ dài cung CH làCâu 124:
Cho tam giác ABC (AB<AC) có ba góc nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AB, AC theo thứ tự tại E, F. Gọi H là giao điểm của BF và CE, I là giao điểm của AH và BC. Từ A kẻ tiếp tuyến AN, AM đến đường tròn (O) với N, M là các tiếp điểm (N, B không cùng nửa mặt phẳng bờ AO).
a) Chứng minh các điểm A, I, M, N, O cùng thuộc một đường tròn
 Xem đáp án
Xem đáp án
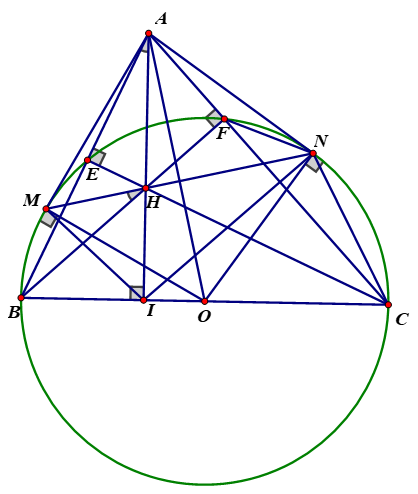
Các điểm A, I, M, N, O cùng thuộc một đường tròn.
Vì (Vì AM, AN là tiếp tuyến với đường tròn (O)).
 nên
nên
Suy ra tứ giác ANOM nội tiếp (Tổng hai góc đối bằng 180o) (1)
(Vì E, F thuộc đường tròn đường kính BC).
Khi đó H là trực tâm tam giác ABC,
Nên, do đó
Suy ra tứ giác AIOM nội tiếp (Tổng hai góc đối bằng 180o) (2)
Từ (1) và (2) suy ra A, I, M, N, O cùng nằm trên một đường tròn.Câu 125:
2. Chứng minh
 Xem đáp án
Xem đáp án
2. Chứng minh .
Ta có: AM=AN(tính chất hai tiếp tuyến cắt nhau) nên cân tại A
Suy ra .
Mà (cùng chắn cung của đường tròn đường kính AO).
Vậy .
Câu 126:
 Xem đáp án
Xem đáp án
Chứng minh ba điểm M, H, N thẳng hàng.
Ta có: (g.g) (1).
Mà (g.g) (2).
Từ (1) và (2) ta có: (c.g.c).
mà (cmt)
Hai tia NH và NM trùng nhau hay M, H, N thẳng hàng.
Câu 127:
Cho đường tròn (O;R) có dây MN cố định (MN<2R), P là một điểm trên cung lớn MN sao cho tam giác MNP có ba góc nhọn. Các đường cao ME và NK của tam giác MNP cắt nhau tại H.
a) Chứng minh rằng tứ giác PKHE nội tiếp đường tròn
 Xem đáp án
Xem đáp án
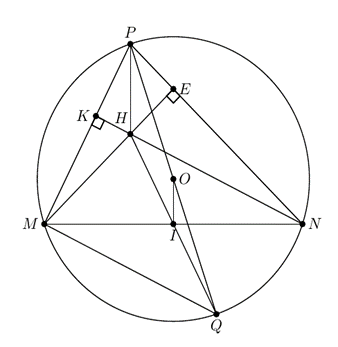
Chứng minh rằng tứ giác PKHE nội tiếp đường tròn.
Ta có: (gt).
.
Tứ giác PKHE nội tiếp đường tròn.
Kéo dài PO cắt đường tròn tại O. Chứng minh .
Ta có: (góc nội tiếp chắn nửa đường tròn (O)).
mà .
.
(so le trong).
Mà (hai góc nội tiếp cùng chắn cung )
Câu 128:
c) Chứng minh rằng khi P thay đổi trên đường tròn (O) thì độ dài đoạn PH không đổi.
 Xem đáp án
Xem đáp án
c) Chứng minh rằng khi P thay đổi trên đường tròn (O) thì độ dài đoạn PH không đổi.
Gọi I là trung điểm và OI là đường trung bình của
Ta có:
Mà MI không đổi và không đổi.
không đổi không đổi.
Câu 129:
 Xem đáp án
Xem đáp án
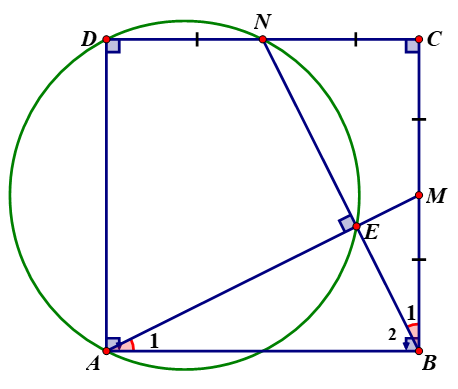
Dễ thấy (hai cạnh góc vuông)
Suy ra (tương ứng)
Mà
Suy ra vuông tại E.
Xét tứ giác ADNEcó nội tiếp đường tròn đường kính
Câu 130:
Cho tam giác nhọn ABC nội tiếp đường tròn (O) (AB<AC). Gọi H là trực tâm tam giác ABC, gọi L là giao điểm của AH với đường tròn (O). Lấy điểm F bất kì trên cung nhỏ LC (không trùng với L và C). Lấy điểm K sao cho đường thẳng AClà trung trực của FK.
1) Chứng minh tứ giác AHCK nội tiếp đường tròn
 Xem đáp án
Xem đáp án
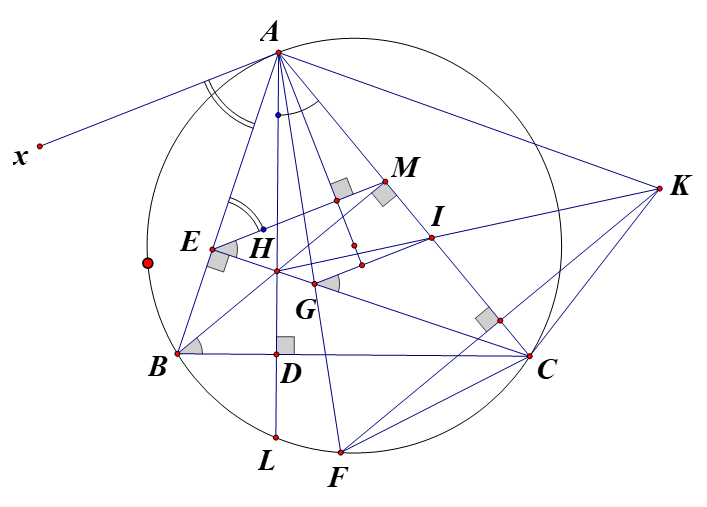
1) Gọi AD , BM và CE là ba đường cao của tam giác ABC
Tứ giác BEHD nội tiếp
Suy ra tứ giác AHCK nội tiếp
Câu 131:
 Xem đáp án
Xem đáp án
2) Kẻ tiếp tuyến Ax với (O) ta có
Xét tg AHGI có
suy ra AHGI nội tiếp
Từ (1) và (2) suy ra điều phải chứng minh .
Câu 132:
Cho nửa đường tròn tâm O đường kính AB Dựng tiếp tuyến Ax (Ax và nửa đường tròn cùng thuộc nửa mặt phẳng bờ AB). C là một điểm nằm trên nửa đường tròn (C không trùng A, B), dựng tiếp tuyến Oy của nửa đường tròn (O) cắt Ax tại D. Kẻ , BD cắt (O) tại điểm thứ hai là K và cắt CH tại M. Gọi J là giao điểm của OD và AC.
a) Chứng minh rằng tứ giác AKMH nội tiếp được một đường tròn.
 Xem đáp án
Xem đáp án
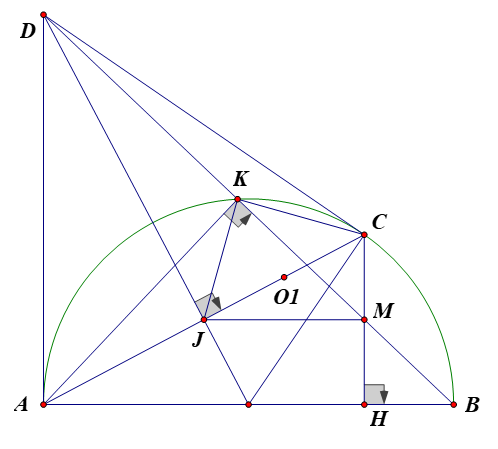
Chứng minh rằng tứ giác AKMH nội tiếp được một đường tròn.
Ta có: (góc nội tiếp chắn nửa đường tròn tâm O).
Có (giả thiết) nên .
Xét tứ giác AKMH có .
Mà hai góc ở vị trí đối nhau nên tứ giác AKMH là tứ giác nội tiếp.
Câu 133:
b) Chứng minh rằng tứ giác CKJM nội tiếp được một đường tròn .
 Xem đáp án
Xem đáp án
Chứng minh rằng tứ giác CKJM nội tiếp được một đường tròn (O).
Do DA, DC là hai tiếp tuyến của đường tròn (O) nên ta có DA=DC. Suy ra D nằm trên trung trực của đoạn AC.
Mà OA=OC=R nên O cũng nằm trên trung trực của AC.
Do đó, đường thẳng OD là đường trung trực của đoạn thẳng AC hay .
Suy ra .
Xét tứ giác ẠJKD có .
Suy ra tứ giác ẠJKD nội tiếp đường tròn đường kính AD.
Do đó, ta có (hai góc cùng bù với ).
Xét đường tròn (O) có (góc tạo bởi tiếp tuyến và dây cung chắn cung ).
Có (góc nội tiếp chắn cung ).
Xét tam giác ACH có , suy ra .
Nên, ta có
Suy ra .
Vậy tứ giác CKJM có hay , nên tứ giác CKJM là tứ giác nội tiếp.
Câu 134:
 Xem đáp án
Xem đáp án
Chứng minh rằng DJ là tiếp tuyến của đường tròn (O1).sđ
Theo chứng minh trên CKJM là tứ giác nội tiếp, suy ra .
Mà (các góc nội tiếp cùng chắn cung ).
Nên ta có được ở vị trí đồng vị. Suy ra .
Mà nên ta có .
Vậy tứ giác CKJM nội tiếp đường tròn đường kính JC.
Theo chứng minh trên, ta có hay .
Do đó DJ là tiếp tuyến của đường tròn .
Câu 135:
Cho đường tròn (O) đường kính AB, lấy điểm C trên đường tròn (O) sao cho BC < AC. Gọi d là tiếp tuyến tại B của đường tròn (O), kẻ đường kính CD, các đường thẳng AC, AD lần lượt cắt d tại E,F. Đường thẳng qua A vuông góc với CD tại K cắt EF tại I
 Xem đáp án
Xem đáp án
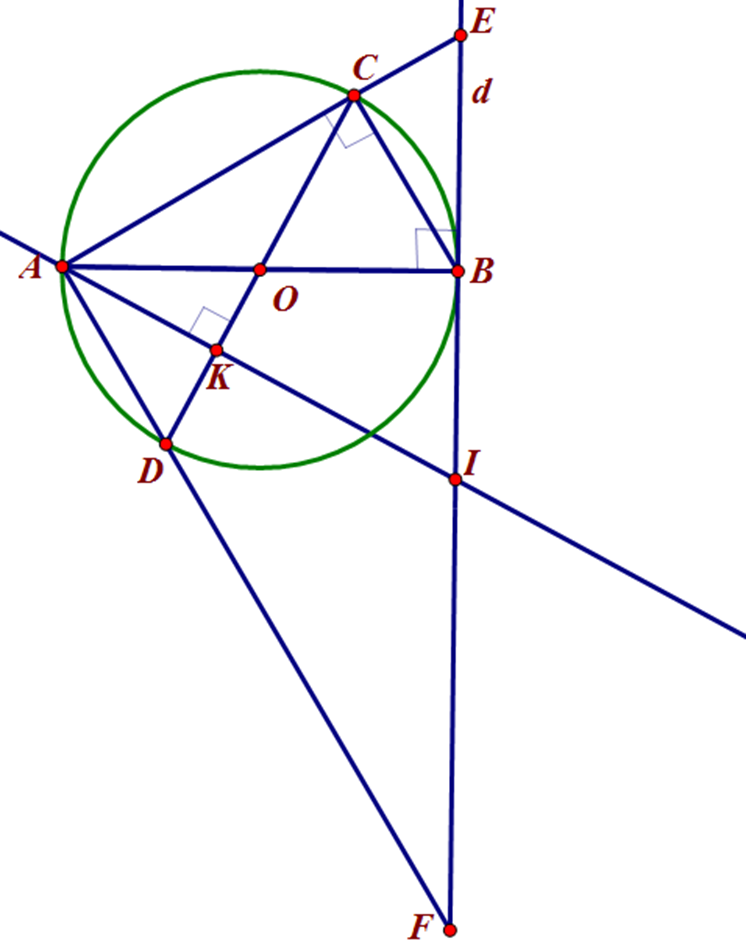
1) Chứng minh tứ giác OBIK nội tiếp.
Tứ giác OKIB nội tiếp
Câu 136:
2. Chứng minh AC.AE=AD.AF
 Xem đáp án
Xem đáp án
2) Chứng minh AC.AE = AD.AF.
- Ta có (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC)
phụ với
phụ với
- Mà
- Xét có
chung
đồng dạng
(đpcm)
Câu 137:
 Xem đáp án
Xem đáp án
- Ta có:
( đồng dạng chứng minh trên)
(cùng phụ với )
cân tại (1)
- Ta có:
(đồng dạng chứng minh trên)
(cùng phụ với )
cân tại I
- Từ (1)và (2) là trung điểm của EF
Câu 138:
 Xem đáp án
Xem đáp án
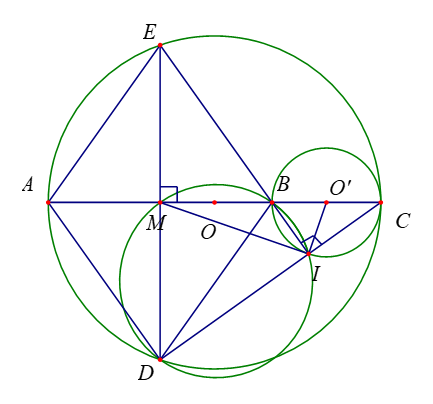
1. Áp dụng hệ thức lượng trong tam giác ta có:
·
·
Câu 139:
 Xem đáp án
Xem đáp án
2. Tứ giác BMDI có:
(gt)
(gt)
Tứ giác BMDI nội tiếp.
Câu 140:
 Xem đáp án
Xem đáp án
3. Tứ giác ADBE có:
Tứ giác ADBE là hình thoi
· Ta có:
Mà
Nên I, B, Ethẳng hàng.
Câu 141:
4. Gọi O là tâm đường tròn đường kính BC. Chứng minh MI là tiếp tuyến của đường tròn O.
 Xem đáp án
Xem đáp án
4. Ta có O' là tâm đường tròn đường kính BC nên O' là trung điểm của BC.
Nên ta có:
Mà
Vậy MI là tiếp tuyến của đường tròn O.
Câu 142:
Cho tam giác ABC vuông tại A đường cao AH. đường tròn tâm E đường kính BH cắt AB tại M (M khác B), đường tròn tâm F đường kính HC cắt AC tại N (N khác C).
1. Chứng minh AM.AB=AN.AC và
 Xem đáp án
Xem đáp án
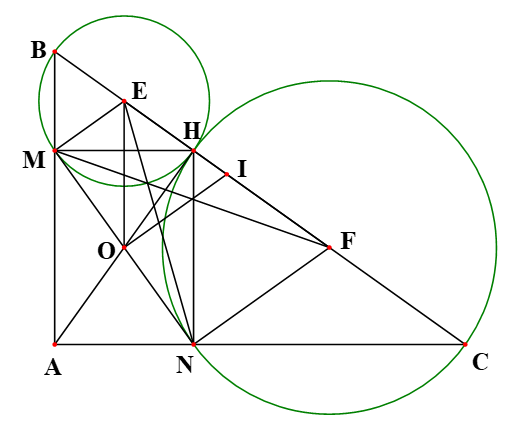
1. Ta có: (các góc nội tiếp chắn nửa đường tròn)
Áp dụng hệ thức lượng vào các tam giác vuông AHB và AHC, có:
và
Mặt khác, tứ giác AMHN có ba góc vuông nên là hình chữ nhật .
Câu 143:
 Xem đáp án
Xem đáp án
2. Tứ giác AMHN là hình chữ nhật, có O là giao điểm của AH và MN
O là trung điểm của AH và MN
Dễ thấy (c.c.c)
Chứng minh tương tự được
là hình thang vuông
Lại có OI là đường trung bình của hình thang vuông MEFN
Câu 144:
3. Chứng minh
 Xem đáp án
Xem đáp án
3. Đặt MN=AH=h; x, y lần lượt là bán kính của (E) và (F). Ta có:
Vậy .
Câu 145:
Cho điểm M nằm bên ngoài đường tròn (O; R). Từ điểm M kẻ hai tiếp tuyến MA,MB với đường tròn đó ( A, B là các tiếp điểm ). Qua điểm A kẻ đường thẳng song song với MB cắt đường tròn (O;R) tại C. Nối MC cắt đường tròn (O; R) tại D. Tia AD cắt MB tại E .
a) Chứng minh MAOB là tứ giác nội tiếp.
 Xem đáp án
Xem đáp án
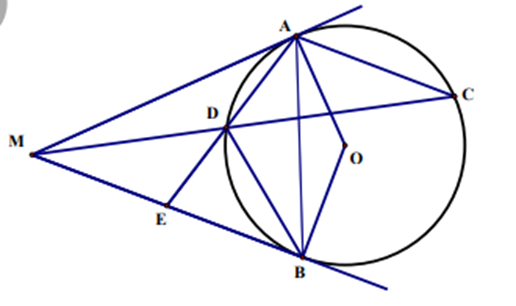
Xét tứ giác MAOB có (MA, MB là các tiếp tuyến của (O)) .
.
Suy ra MAOB là tứ giác nội tiếp.
Câu 146:
 Xem đáp án
Xem đáp án
Xét và có chung và (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung ) .
.
Xét và có chung.
Mà (so le trong).
Mặt khác (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung ).
.
.
Từ .
Câu 147:
c) Xác định vị trí của điểm M để
 Xem đáp án
Xem đáp án
c) Ta có (hai góc nội tiếp cùng chắn cung ).
Mà .
Ta có .
đi qua O và D là điểm chính giữa cung nhỏ .
đều vuông tại B có .
.
Câu 148:
Cho đường tròn tâm O, bán kính R. Từ điểm C nằm ngoài đường tròn kẻ hai tiếp tuyến CA, CB và cát tuyến CMN với đường tròn (O) (A, B là hai tiếp điểm, M nằm giữa C và N). Gọi H là giao điểm của CO và AB.
a) Chứng minh tứ giác AOBC nội tiếp.
 Xem đáp án
Xem đáp án
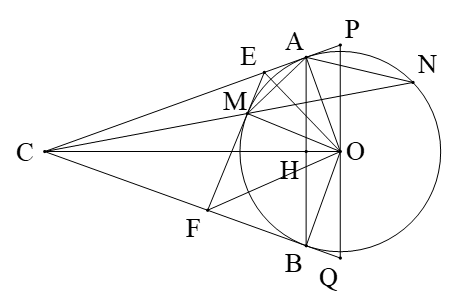
a) (Do CA là tiếp tuyến của (O) ở A).
(Do CB là tiếp tuyến của (O) ở B).
.
Vậy tứ giác AOBC là tứ giác nội tiếp.
Câu 149:
 Xem đáp án
Xem đáp án
b) Xét và có:
là góc chung
(Hệ quả góc tạo bởi tia tiếp tuyến và dây cung ).
Do đó đồng dạng với (g.g)
![]() .
.
Mặt khác ta có: CA=CB ( tính chất hai tiếp tuyến cắt nhau)
là đường trung trực của tại H.
Xét vuông ở A có .
Từ (1) và (2) suy ra: .
Câu 150:
c) Tiếp tuyến tại M của đường tròn (O) cắt CA, CB theo thứ tự tại E, F. Đường thẳng vuông góc với CO tại O cắt CA, CB theo thứ tự tại P, Q. Chứng minh .
 Xem đáp án
Xem đáp án
c) Theo tính chất hai tiếp tuyến cắt nhau và tính chất góc ngoài của tam giác ta có:
Câu 151:
d) Chứng minh rằng:
 Xem đáp án
Xem đáp án
d) Xét và có: (câu c). Tương tự: .
Do đó POE đồng dạng với .
Áp dụng bất đẳng thức Côsi ta có:
( đpcm)
Câu 152:
 Xem đáp án
Xem đáp án
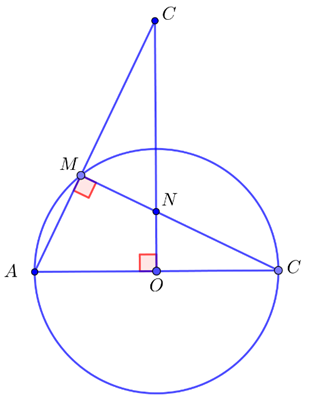
1. Chứng minh tứ giác AOMN nội tiếp được một đường tròn.
Xét tứ giác AOMN có
nội tiếp được một đường tròn.
Câu 153:
 Xem đáp án
Xem đáp án
2. Chứng minh rằng: .
Xét và
Có ( đối đỉnh):
( g-g)
Câu 154:
3. Tính góc , tính diện tích tam giác ABC theo R.
 Xem đáp án
Xem đáp án
3. Khi góc , tính diện tích tam giác ABC
.
Câu 155:
Cho tứ giác ABCD nội tiếp. Gọi I là giao điểm của AC và BD. Kẻ
a) Chứng minh rằng tứ giác AHIK nội tiếp.
 Xem đáp án
Xem đáp án
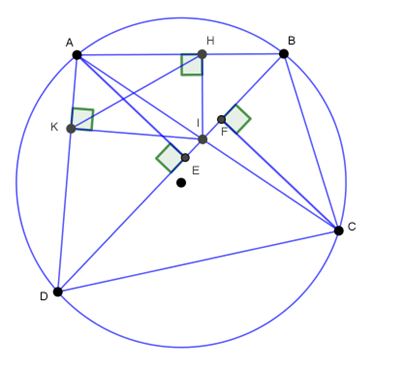
a) Ta có (gt)
Mà hai góc ở vị trí đối nhau, nên tứ giác AHIK là tứ giác nội tiếp (dhnb)
Câu 156:
b) Chứng minh rằng: IA.IC=IB.ID
 Xem đáp án
Xem đáp án
b) Xét tam giác và có:
(do tứ giác ABCD nội tiếp )
(2 góc đối đỉnh)
Suy ra (g.g)
.
Câu 157:
 Xem đáp án
Xem đáp án
c) Ta có (do tứ giác AHIK nội tiếp)
mà (do tứ giác ABCD nội tiếp)
suy ra .
Tương tự ta có (do tứ giác AHIK nội tiếp)
và (do tứ giác ABCD nội tiếp)
suy ra
Xét hai tam giác và có:
(cmt)
(cmt)
Suy ra (g.g)
Câu 158:
 Xem đáp án
Xem đáp án
d) Gọi S1 là diện tích tam giác .
Vì nên
Vẽ
và có chung cạnh đáy BD nên:
Từ (1) và (2) suy ra
(đpcm)
Câu 159:
Cho đường tròn tâm O, đường kính AB=2R, C là điểm chính giữa cung AB. Hai tiếp tuyến với đường tròn (O) tại A và C cắt nhau ở D.
1. Chứng minh AOCD là hình vuông.
 Xem đáp án
Xem đáp án
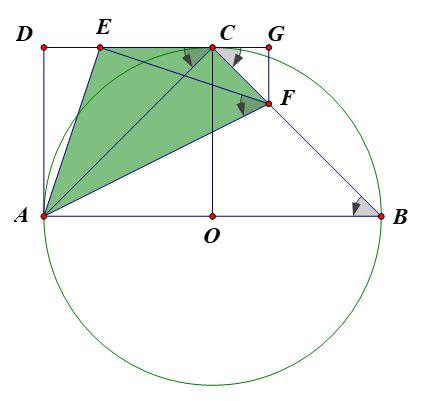
1. C là điểm chính giữa cung AB nên hay .
Do AD và CD là các tiếp tuyến tại A, C của đường tròn (O) nên ta có: , , hay .
Suy ra, tứ giác AOCD có và OA=OC=R. Do đó, tứ giác AOCD là hình vuông.
Câu 160:
 Xem đáp án
Xem đáp án
2) Diện tích phần nằm ngoài hình thang ABCD của hình tròn (O) được chia thanh hai phần:
Phần 1: nửa đường tròn đường kính AB, không chứa điểm C, có diện tích là .
Phần 2: hình viên phân nằm ngoài tam giác vuông cân OBC, có diện tích là .
Vậy, diện tích cần tính có giá trị là:
(đơn vị diện tích).
Câu 161:
3. Trên đoạn DC lấy điểm E sao cho . Trên đoạn BC lấy điểm F sao cho EF=EA. Kẻ FG vuông góc với đường thẳng DC (). Tính độ dài đoạn thẳng CG theo R.
 Xem đáp án
Xem đáp án
3) Tính độ dài đoạn thẳng CD theo R?
Theo chứng minh câu a, ta có: .
Từ giả thiết, ta có: .
Xét tam giác ADE vuông tại D có: .
Do CG//AB nên .
Vậy, tam giác CGF có nên tam giác CGF vuông cân tại CGF.
Do đó, .
Xét tam giác vuông EGF có
Nên theo định lý Pythagore, ta có:
do R+x>0
Vậy, ta có .
Câu 162:
4. Chứng minh AECF nội tiếp
 Xem đáp án
Xem đáp án
4) Chứng minh AECF là tứ giác nội tiếp?
Ta chứng minh được nên .
Mà trong tam giác vuông ADE, ta có: . Suy ra .
Ta có: .
Xét tam giác AEF có , AE=EF, nên tam giác AEF vuông cân tại E. Từ đó, ta có .
Xét đường tròn tâm O có là góc tạo bởi tiếp tuyến và dây cung chắn cung AC, nên .
Vậy, tứ giác AECF có , tức là 2 đỉnh liền kề C, F cùng nhìn đoạn AE dưới các góc như nhau. Do đó, tứ giác AECF là tứ giác nội tiếp.
Câu 163:
Cho nửa đường tròn (O; R) đường kính AB. Một điểm M cố định thuộc đoạn thẳng OB Đường thẳng d vuông góc với AB tại M cắt nửa đường tròn đã cho tại N. Trên cung NB lấy điểm E bất kì Tia BE cắt đường thẳng d tại C đường thẳng AC cắt nửa đường tròn tại D Gọi H là giao điểm của AE và đường thẳng d
a) Chứng minh tứ giác BMHE nội tiếp được đường tròn.
 Xem đáp án
Xem đáp án
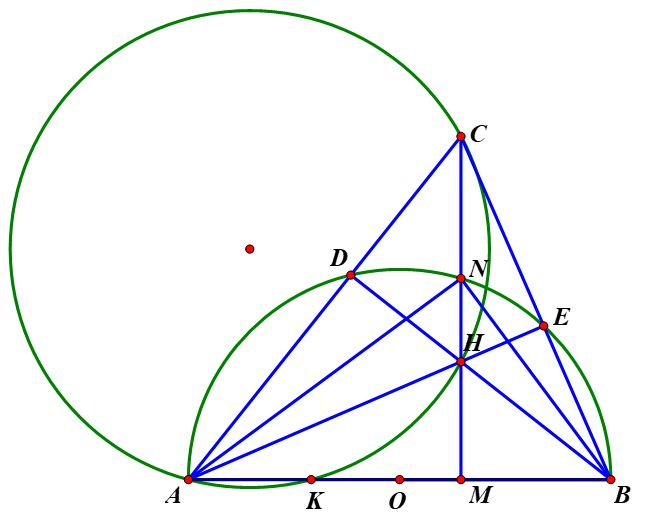
a) Chứng minh tứ giác BMHE nội tiếp được đường tròn.
(góc nội tiếp chắn cung nửa đường tròn)
Trong tứ giác BMHE có tổng hai góc đối bằng 180o nên tứ giác BMHE nội tiếp đường tròn.
Câu 164:
 Xem đáp án
Xem đáp án
b) Chứng minh 3 điểm B, H, D thẳng hàng.
Ta có (góc nội tiếp chắn cung nửa đường tròn)
là đường cao
có 2 đường cao CM và AE cắt nhau tại là trực tâm của đpcm.Câu 165:
 Xem đáp án
Xem đáp án
c) Tính giá trị của biểu thức theo R
Ta có (góc nội tiếp chắn cung nửa đường tròn)
vuông tại N
Áp dụng hệ thức lượng trong vuông tại N ta có
(g-g)
Suy ra
Câu 166:
d) Đường tròn ngoại tiếp tam giác AHC cắt AB tại K. Chứng minh rằng khi E di động trên cung NB thì độ dài đoạn thẳng BK không đổi.
 Xem đáp án
Xem đáp án
d) Đường tròn ngoại tiếp tam giác AHC cắt AB tại ![]() Chứng minh rằng khi E di động trên cung NB thì độ dài đoạn thẳng BK không đổi.
Chứng minh rằng khi E di động trên cung NB thì độ dài đoạn thẳng BK không đổi.
Ta có: (góc nội tiếp cùng chắn cung HK trong đường tròn (AHC))
(cùng phụ ).
Suy ra là phân giác
có CM vừa là đường cao vừa là phân giác
là trung điểm
Do M cố định, B cho trước nên KB không đổi.
Câu 167:
Cho đường tròn tâm O đường kính AB và điểm C(C không trùng với A và B ). Lấy điểm D thuộc đoạn AC (D không trùng với A và C). Tia BD cắt cung nhỏ AC tại điểm M, tia BC cắt tia AM tại điểm N.
1. Chứng minh MNCD là tứ giác nối tiếp.
 Xem đáp án
Xem đáp án
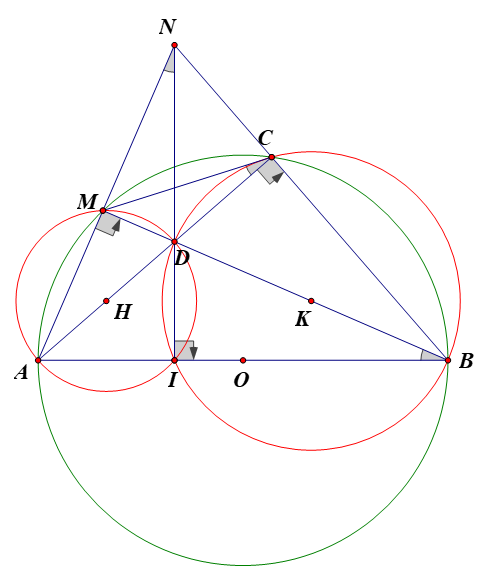
1. Có (góc nội tiếp chắn nửa đường tròn)
Nên suy ra nên MNCD là tứ giác nội tiếp
Câu 169:
 Xem đáp án
Xem đáp án
3. Chứng minh ba điểm N, D, I thẳng hàng.
Ta có (góc nội tiếp chắn nửa đường tròn).
.
Theo chứng minh câu 1, MNCD là tứ giác nội tiếp nên ta có: (2 góc nội tiếp cùng chắn cung MD). (1)
Xét đường tròn tâm O có (2 góc nội tiếp cùng chắn cung MA). (2)
Từ (1) và (2), ta có: .
Mặt khác, ta có:
Tam giác MND vuông tại M nên .
Tam giác MAB vuông tại M nên .
Do đó, ta có: .
Mà (chứng minh trên), nên ta có: .
Do MAID là tứ giác nội tiếp nên ta có: hay
Suy ra .
Vậy, các điểm N, D, I thẳng hàng
Câu 170:
 Xem đáp án
Xem đáp án
Hình vẽ phục vụ câu a: 0,25, câu b: 0,25
(không có hình không chấm)
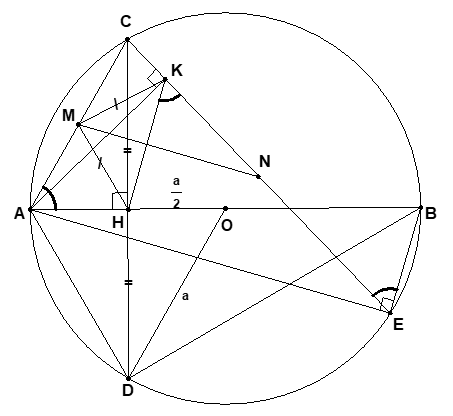
+Tam giác OAD có OA = OD
+Vì H là trung điểm OA và nên DA = DO.Câu 171:
 Xem đáp án
Xem đáp án
Câu 172:
 Xem đáp án
Xem đáp án
c) Chứng minh JL vuông góc với BD
+ IJ//CD và H là trung điểm của CD. Suy ra P là trung điểm của IJ
Ta có: và . Suy ra hai tam giác PIL và PQI đồng dạng.
Do đó: .Mà PI=PJ nên
Lại có nên hai tam giác PIJ và PQL đồng dạng (1).
(đồng vị, tia PQ không nằm trong góc ).
Mà J là trung điểm của BD nên P là trung điểm của HB. Suy raQ là trung điểm của HD.
Do đó JP hay tam giác PQL vuông tại J (2).
Từ (1) và (2) suy ra tam giác PJL vuông tại L. Mà PQ//BD nên JL vuông góc BD.
Câu 173:
Cho đường tròn (O) có tâm O, đường kính BC. Lấy một điểm A trên đường tròn (O) sao cho AB>AC. Từ A, vẽ AH vuông góc với BC (H thuộc BC). Từ H, vẽ HE vuông góc với AB và HF vuông góc với AC (E thuộc AB, F thuộc AC).
a) Chứng minh rằng AEHF là hình chữ nhật và OA vuông góc với EF.
 Xem đáp án
Xem đáp án
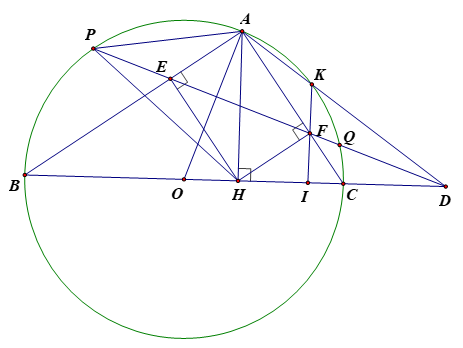
a) Tứ giác AEHF là hình chữ nhật vì có 3 góc vuông
(vì AEHF là hình chữ nhật)
(vì OA=OC)
Do đó :
Câu 174:
 Xem đáp án
Xem đáp án
b)
Do đó:
Ta có: (hệ thức lượng vuông tại H, có HE là chiều cao)
cân tại A.
Câu 175:
 Xem đáp án
Xem đáp án
c)
Do đó
Tứ giác AEFK nội tiếp.
Câu 176:
 Xem đáp án
Xem đáp án
d) Ta có: (hệ thức lượng trong vuông tại H, có HF là chiều cao)
Ta có: (hệ thức lượng trong vuông tại H, có HK là chiều cao)
Từ đó ta có tứ giác AFCD nội tiếp
Vậy ta có: và
Câu 177:
Cho tam giác ABC không có góc tù (AB<AC), nội tiếp đường tròn (O;R) (B, C cố định, A di động trên cung lớn BC). Các tiếp tuyến tại B và C cắt nhau tại M. Từ M kẻ đường thẳng song song với AB, đường thẳng này cắt (O) tại D và E (D thuộc cung nhỏ BC), cắt BC tại F, cắt AC tại I
a) Chứng minh . Từ đó suy ra MBIC là tứ giác nội tiếp.
 Xem đáp án
Xem đáp án
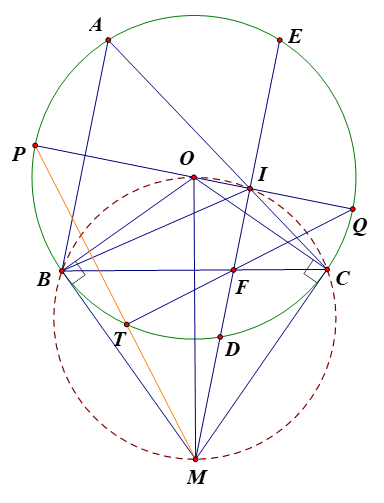
Câu 179:
 Xem đáp án
Xem đáp án
c) Ta có dó PQ là đương kính và có 2 góc đối đỉnh F bằng nhau và (vì )
Nên mà (I nhìn OM dưới goc 90o)
Nên P, T, M thẳng hàng vì
Câu 180:
 Xem đáp án
Xem đáp án
d) Ta có BC không đổi. Vậy diện tích lớn nhất khi và chỉ khi khoảng cách từ I đến BC lớn nhất. Vậy I trùng với O là yêu cầu của bài toán vì I nằm trên cung BC của đường tròn đường kính OM. Khi I trùng O thì vuông tại B. Vậy diện tích lớn nhất khi và chỉ khi AC là đường kính của đường tròn (O; R).
Cách khác
O' là trung điểm của OM. BC cắt OO'; O'T lần lượt tại L và T
Vẽ IH vuông BC tại H
Câu 182:
 Xem đáp án
Xem đáp án
Ta có BD=BA và BE=BF nên
EF//DA và (do BD=BA) suy ra ADEF là hình thang cân
ADEF nội tiếp được (1).
Ta có CK=CD và CA=CE nên
KD//AE và (do CE=CA)
là hình thang cân
nội tiếp được (2).
(1), (2) 4 điểm D, E, F và K cùng thuộc đường tròn ngoại tiếp .
Câu 183:
Cho tam giác ABC(AB<AC) nội tiếp đường tròn đường kính BC, có đường cao AH (H thuộc cạnh BC), đường phân giác trong của góc A trong tam giác ABC cắt đường tròn đó tại K (K khác A). Biết .Tính
 Xem đáp án
Xem đáp án
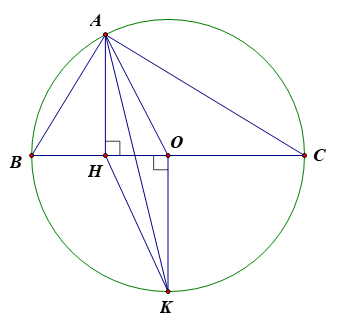
Câu 184:
 Xem đáp án
Xem đáp án
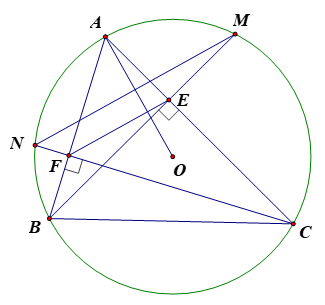
Câu 185:
 Xem đáp án
Xem đáp án
b) Ta có: Tứ giác BCEF nội tiếp (cmt).
(hai góc nội tiếp cùng chắn )
Ta lại có:
(2) (góc nội tiếp cùng chắn )
Từ (1) và (2)
Mà hai góc này ở vị trí đồng vị
Câu 186:
 Xem đáp án
Xem đáp án
d) Ta có (hai góc nội tiếp cùng chắn )
Ta lại có OM=ON
là đường trung trực của MN
Mà MN//EF(cmt)
Câu 187:
Một bình hình trụ có đường kính đáy 1dm, chiều cao 2dm bên trong có chứa viên bi hình cầu có bán kính 4 cm. Hỏi phải đổ vào bình bao nhiêu lít nước để nước đầy bình. Cho biết:
với r là bán kính đáy; h là chiều cao hình trụ.
với R là bán kính hình cầu.
 Xem đáp án
Xem đáp án
Thể tích bình hình trụ:
Thể tích viên bi hình cầu:
Số lít nước đổ vào đầy bình: (lít)
Câu 188:
Kính lão đeo mắt của người già thường là loại thấu kính hội tụ. Bạn An đã dùng một chiếc kính lão của ông ngoại để tạo ra hình ảnh của một cây nến trên một tấm màn. Xét cây nến là một vật sáng có hình dạng là đoạn AB đặt vuông góc với trục chính của một thấu kính hội tụ, cách thấu kính một đoạn OA=2cm. Thấu kính có quang tâm O và tiêu điểm F. Vật AB cho ảnh thật A'B' gấp 3 lần AB. Tính tiêu cự (OF') của thấu kính ? Biết rằng đường đi của tia sáng được mô tả trong hình vẽ sau :
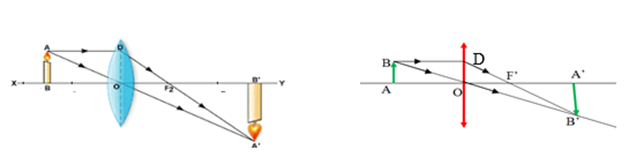
 Xem đáp án
Xem đáp án
Vì AB//A'B; nên theo hệ quả định lí TaLet, ta được :
Vì OD//A'B' nên theo hệ quả định lí TaLet, ta được :
Vậy tiêu cự của thấu kính : (m)
Câu 189:
 Xem đáp án
Xem đáp án
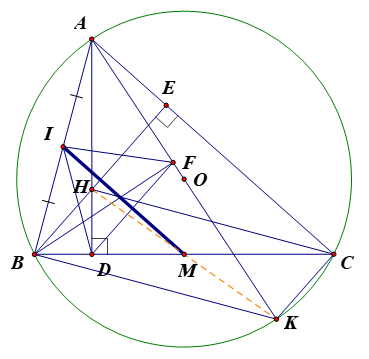
Câu 190:
 Xem đáp án
Xem đáp án
b) Ta có : nội tiếp đường tròn (O) có AK là đường kính
vuông tại B và vuông tại C.
Mà H là trực tâm (AD, BE là hai đường cao cắt nhau tại H)
(cùng vuông góc với AB) và (cùng vuông góc với AC)
Tứ giác BHCK là hình bình hành.
Có M là trung điểm của đường chéo BC nên M cũng là trung điểm của đường chéo HK.
Vậy 3 điểm H, M, K thẳng hàng.
Câu 191:
 Xem đáp án
Xem đáp án
c) Ta có:
+) BE//CK (cmt) (hai góc so le trong).
+) (hai góc nội tiếp cùng chắn )
+) (Tứ giác ABDF nội tiếp)
Nên mà 2 góc này ở vị trí đồng vị suy ra BE//DF
Ta lại có: IM là đường trung bình của (I, M lần lượt là trung điểm của AB và BC)
Mà nên (1)
Ta có: ID, IF lần lượt là 2 đường trung tuyến của 2 tam giác ABD và ABF ứng với cạnh huyền (2)
Từ (1) và (2) suy ra IM là đường trung trực của DF