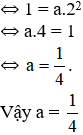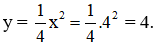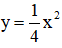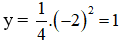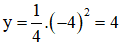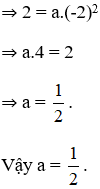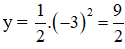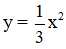5 câu hỏi trắc nghiệm thuộc Luyện tập 38 - 39

Câu 1:

Cho hàm số y = f(x) = x².

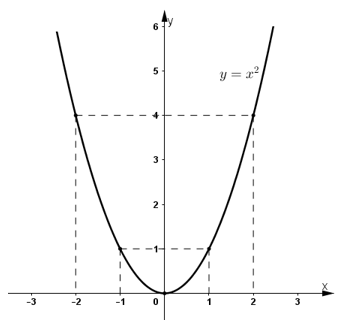
a) Vẽ đồ thị của hàm số đó.

b) Tính các giá trị f(-8); f(-1,3); f(-0,75); f(1,5).

c) Dùng đồ thị để ước lượng các giá trị (0,5)²; (-1,5)²; (2,5)².

d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số √3 ; √7.

Xem đáp án

a) Ta có bảng giá trị:

x	-2	-1	0	1	2
y = x²	4	1	0	1	4

Vẽ đồ thị hàm số :

Trên hệ trục tọa độ xác định các điểm (-2 ; 4) ; (-1 ; 1) ; (0 ; 0) ; (1 ; 1) ;

(2 ; 4). Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số y = x².

b) f(-8) = (-8)² = 64

f(-1,3) = (-1,3)² = 1,69

f(-0,75) = (-0,75)² = 0,5625

f(1,5) = (1,5)² = 2,25.

c)

– Để ước lượng giá trị (0,5)² ta tìm điểm A thuộc đồ thị có hoành độ là 0,5.

Khi đó, tung độ của điểm A chính là giá trị (0,5)². Từ điểm (0,5;0) trên trục

hoành ta kẻ đường thẳng song song với Oy cắt đồ thị tại điểm A. Từ điểm A

trên đồ thị kẻ đường thẳng song song với Ox ta xác định được giá trị của (0,5)²

– Để ước lượng giá trị (-1,5)² ta tìm điểm B thuộc đồ thị có hoành độ là -1,5.

Khi đó, tung độ của điểm B chính là giá trị (-1,5)². Từ điểm (-1,5;0) trên trục

hoành ta kẻ đường thẳng song song với Oy cắt đồ thị tại điểm B. Từ điểm B

trên đồ thị kẻ đường thẳng song song với Ox ta xác định được giá trị của (-1,5)²

– Để ước lượng giá trị (2,5)² ta tìm điểm C thuộc đồ thị có hoành độ là 2,5.

Khi đó, tung độ của điểm C chính là giá trị (2,5)². Từ điểm (2,5;0) trên trục

hoành ta kẻ đường thẳng song song với Oy cắt đồ thị tại điểm C. Từ điểm C

trên đồ thị kẻ đường thẳng song song với Ox ta xác định được giá trị của (2,5)²

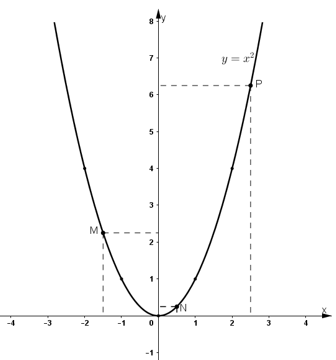
Trên đồ thị hàm số, lấy các điểm M, N, P có hoành độ lần lượt bằng

-1,5 ; 0,5 và 2,5.

Dựa vào đồ thị nhận thấy các điểm M, N, P có tọa độ là : M(-1,5 ; 2,25) ;

N(0,5 ; 0,25) ; P(2,5 ; 6,25).

Vậy (0,5)² = 2,25 ; (-1,5)² = 2,25 ; (2,5)² = 6,25.

d)

– Để ước lượng vị trí điểm biểu diễn số √3 trên trục hoành ta tìm điểm M

thuộc đồ thị có tung độ là (√3)² = 3. Khi đó, hoành độ của điểm M

chính là vị trí điểm biểu diễn √3. Từ điểm (0;3) trên trục tung ta kẻ

đường thẳng song song với Ox cắt đồ thị tại điểm M. Từ điểm M

trên đồ thị kẻ đường thẳng song song với Oy ta xác định được

hoành độ của điểm M chính là vị trí điểm biểu diễn √3

– Để ước lượng vị trí điểm biểu diễn số √7 trên trục hoành ta tìm điểm N

thuộc đồ thị có tung độ là (√7)² = 7. Khi đó, hoành độ của điểm N chính

là vị trí điểm biểu diễn √7. Từ điểm (0;7) trên trục tung ta kẻ đường

thẳng song song với Ox cắt đồ thị tại điểm N. Từ điểm N trên đồ thị kẻ

đường thẳng song song với Oy ta xác định được hoành độ của điểm N

chính là vị trí điểm biểu diễn √7

Ta có : (√3)² = 3 ; (√7)² = 7

⇒ Các điểm (√3 ; 3) và (√7 ; 7) thuộc đồ thị hàm số y = x².

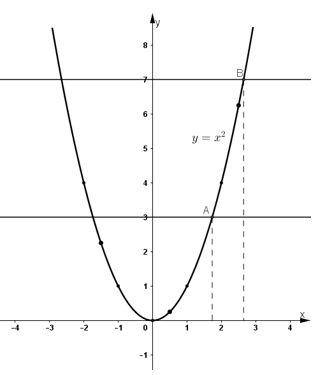
Để xác định các điểm √3 ; √7 trên trục hoành, ta lấy trên đồ thị hàm số

các điểm A, B có tung độ lần lượt là 3 và 7.

Chiếu vuông góc các điểm A, B trên trục hoành ta được

các điểm √3 ; √7 trên đồ thị hàm số.

Câu 2:

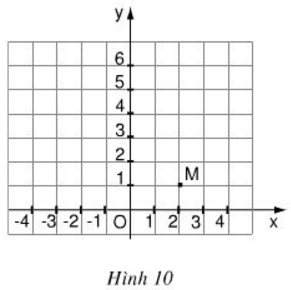
Trên mặt phẳng tọa độ (h.10), có một điểm M thuộc đồ thị của hàm số y = ax².

a) Tìm hệ số a.

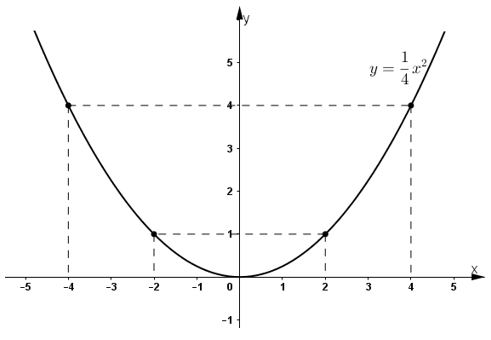
b) Điểm A(4; 4) có thuộc đồ thị không?

c) Hãy tìm thêm hai điểm nữa(không kể điểm O) để vẽ đồ thị.

Xem đáp án

a) Dựa trên hình 10 ta thấy điểm M có tọa độ (2; 1).

M thuộc đồ thị hàm số y = ax²

b) Với x = 4 ta có

Vậy điểm A(4 ; 4) thuộc đồ thị hàm số

c) Chọn x = -2 ⇒

Vậy (-2; 1) thuộc đồ thị hàm số.

Chọn x = -4 ⇒

Vậy (-4; 4) thuộc đồ thị hàm số.

* Vẽ đồ thị:

Câu 3:

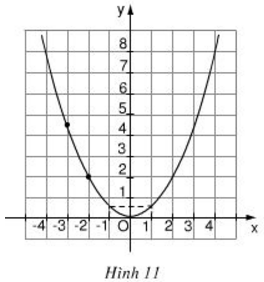
Biết rằng đường cong trong hình 11 là một parapol y = ax².

a) Tìm hệ số a.

b) Tìm tung độ của điểm thuộc parapol có hoành độ x = -3.

c) Tìm các điểm thuộc parapol có tung độ y = 8.

Xem đáp án

a) Ta có đồ thị hàm số y = ax² đi qua điểm (-2 ; 2)

b) Tại x = -3 ta có:

Vậy điểm có hoành độ x = -3 thì tung độ bằng 4,5.

c) Hoành độ các điểm có tung độ y =8 thỏa mãn phương trình:

⇔ x² = 16 ⇔ x = 4 hoặc x = -4.

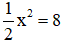
Vậy các điểm thuộc parabol có tung độ bằng 8 là (4; 8) và (-4; 8).

Câu 4:

Cho hai hàm số $y = \frac{1}{3} x^{2}$ và y = -x + 6.

a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.

b) Tìm tọa độ các giao điểm của hai đồ thị đó.

Xem đáp án

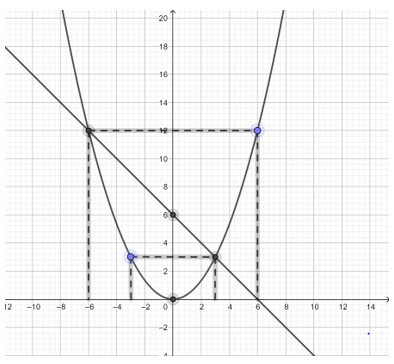
a) - Vẽ đường thẳng y = -x + 6

Cho x = 0 ⇒ y = 6 được điểm (0, 6)

Cho y = 0 ⇒ x = 6 được điểm (6, 0)

⇒ Đường thẳng y = -x + 6 đi qua các điểm (6; 0) và (0; 6).

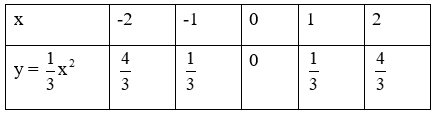
- Lập bảng giá trị và vẽ đồ thị hàm số

⇒ Parabol đi qua các điểm (3; 3); (-3; 3); (-6; 12); (6; 12); (0; 0).

b) Xét phương trình hoành độ giao điểm

Câu 5:

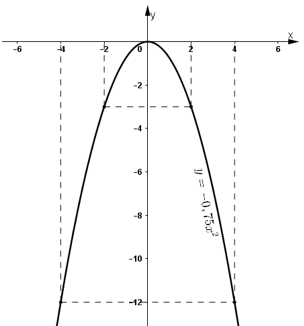
Cho hàm số y = - 0,75x². Qua đồ thị của hàm số đó, hãy cho biết khi x tăng từ -2 đến 4 thì giá trị nhỏ nhất và giá trị lớn nhất của y là bao nhiêu?

Xem đáp án

- Lập bảng giá trị:

x	-4	-2	0	2	4
y = -0,75x²	-12	-3	0	-3	-12

- Vẽ đồ thị:

- Quan sát đồ thị hàm số y = -0,75x²:

Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.

Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4

Giá trị lớn nhất của y = 0 đạt được khi x = 0.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Toán 9 Chương 4: Hàm số y = ax^2 (a ≠ 0) - Phương trình bậc hai một ẩn

Luyện tập 38 - 39

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương