6 câu hỏi trắc nghiệm thuộc Bài 2: Hệ hai phương trình bậc nhất hai ẩn

Câu 1:

Kiểm tra rằng cặp số (x; y) = (2; -1) vừa là nghiệm của phương trình thứ nhất, vừa là nghiệm của phương trình thứ hai.

Xem đáp án

Thay x = 2 , y = -1 vào phương trình 2x + y = 3 ta được:

$\{\begin{cases} V T = 2.2 + (- 1) + 3 \\ V P + 3 \end{cases} \Rightarrow V T = V P$

Vậy (2;-1) là nghiệm của phương trình 2x+y=3

- Thay x = 2, y = -1 vào phương trình x – 2y = 4 ta được:

$\{\begin{array}{l} V T = 2 - 2 . (- 1) = 4 \\ V P = 4 \end{array} \Rightarrow V T = V P$

Vậy (2;-1) là nghiệm của phương trình x – 2y = 4

Vậy cặp số (x; y) = (2; -1) vừa là nghiệm của phương trình thứ nhất, vừa là nghiệm của phương trình thứ hai.

Câu 2:

Tìm từ thích hợp để điền vào chỗ trống (…) trong câu sau: Nếu điểm M thuộc đường thẳng ax + by = c thì tọa độ (xo; yo) của điểm M là một … của phương trình ax + by = c.

Xem đáp án

Nếu điểm M thuộc đường thẳng ax + by = c thì tọa độ (xo; yo) của điểm M là một nghiệm của phương trình ax + by = c.

Câu 3:

Hệ phương trình trong ví dụ 3 có bao nhiêu nghiệm? Vì sao?

Xem đáp án

Hệ phương trình trong ví dụ 3 có vô số nghiệm vì tập nghiệm của hai phương trình trong hệ được biểu diễn bởi cùng một đường thẳng y = 2x – 3

Câu 4:

Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao:

a) $\{\begin{cases} y = 3 - 2 x \\ y = 3 x - 1 \end{cases}$ b) $\{\begin{cases} y = \frac{- 1}{2} x + 3 \\ y = \frac{- 1}{2} x + 1 \end{cases}$

c) $\{\begin{cases} 2 y = - 3 x \\ 3 y = 2 x \end{cases}$ d) $\{\begin{cases} 3 x - y = 3 \\ x - \frac{1}{3} y = 1 \end{cases}$

Xem đáp án

$\{\begin{array}{l} y = 3 - 2 x \\ y = 3 x - 1 \end{array} \Leftrightarrow \{\begin{cases} y = - 2 x + 3 \\ y = 3 x - 1 \end{cases}$

a) Xét (d): y = -2x + 3 có a = -2; b = 3

(d’) : y = 3x – 1 có a’ = 3 ; b’ = -1.

Có a ≠ a’ ⇒ (d) cắt (d’)

⇒ Hệ $\{\begin{cases} y = 3 - 2 x \\ y = 3 x - 1 \end{cases}$ có nghiệm duy nhất.

b) $\{\begin{cases} y = - \frac{1}{2} x + 3 (d) \\ y = - \frac{1}{2} x + 1 (d') \end{cases}$

Xét (d): y = $- \frac{1}{2}$ x + 3 có a = $- \frac{1}{2}$ ; b = 3

(d’): y = $- \frac{1}{2}$ x + 1 có a’ = $- \frac{1}{2}$ ; b’ = 1.

Có a = a’; b ≠ b’ ⇒ (d) // (d’)

⇒ Hệ phương trình $\{\begin{cases} y = - \frac{1}{2} x + 3 \\ y = - \frac{1}{2} x + 1 \end{cases}$ vô nghiệm.

c) Ta có:

$\{\begin{array}{l} 2 y = - 3 x \\ 3 y = 2 x \end{array} \Leftrightarrow \{\begin{cases} y = - \frac{3}{2} x \\ y = \frac{2}{3} x \end{cases}$

Xét (d): y = $\frac{- 3}{2}$ x có a = $\frac{- 3}{2}$ ; b = 0

(d’) : y = $\frac{2}{3}$ x có a’ = $\frac{2}{3}$ ; b’ = 0

Ta có: a ≠ a’ ⇒ (d) cắt (d’)

⇒ Hệ $\{\begin{cases} 2 y = - 3 x \\ 3 y = 2 x \end{cases}$ có nghiệm duy nhất.

d) Ta có:

$\{\begin{cases} 3 x - y = 3 \\ x - \frac{1}{3} y = 1 \end{cases} \Leftrightarrow \{\begin{cases} y = 3 x - 3 \\ \frac{1}{3} y = x - 1 \end{cases} \Leftrightarrow \{\begin{cases} y = 3 x - 3 \\ y = 3 x - 3 \end{cases}$

Ta có: a = a’=3; b = b’ = -3

Nhận thấy hai đường thẳng trên trùng nhau

⇒ Hệ phương trình có vô số nghiệm.

Câu 5:

Đoán nhận số nghiệm của hệ phương trình sau bằng hình học:

a) $\{\begin{cases} 2 x - y = 1 \\ x - 2 y = - 1 \end{cases}$

b) $\{\begin{cases} 2 x + y = 4 \\ - x + y = 1 \end{cases}$

Xem đáp án

a) Xét hệ (I): $\{\begin{cases} 2 x - y = 1 \\ x - 2 y = - 1 \end{cases}$

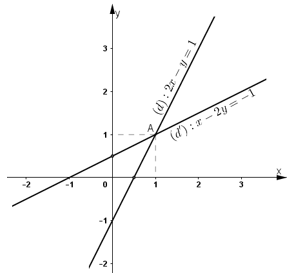
Ta biểu diễn hai đường thẳng (d): 2x – y = 1 và (d’): x – 2y = -1 trên mặt phẳng tọa độ.

+ Xét đường thẳng (d): 2x – y = 1 hay (d) : y = 2x – 1

Chọn x = 0 ⇒ y = -1.

Chọn y = 0 ⇒ x = $\frac{1}{2}$

⇒ (d) đi qua hai điểm (0; -1) và $(\frac{1}{2}; 0)$

+ Xét (d’) : x – 2y = -1 hay (d’): y = $\frac{1}{2}$ x + $\frac{1}{2}$

Chọn x = 0 ⇒ y = $\frac{1}{2}$

Chọn y = 0 ⇒ x = -1.

⇒ (d’) đi qua hai điểm $(0; \frac{1}{2})$ và (-1; 0).

Dựa vào đồ thị thấy hai đường thẳng (d) và (d’) cắt nhau tại A (1; 1).

Thử lại, thay x =1, y=1 vào các phương trình của hệ (I) ta được:

$\{\begin{array}{l} 2.1 - 1 = 1 \\ 1 - 2.1 = - 1 \end{array} \Leftrightarrow \{\begin{cases} 1 = 1 \\ - 1 = - 1 \end{cases}$ (luôn đúng)

Vậy hệ phương trình (I) có một nghiệm là (1; 1).

b) Xét (II): $\{\begin{cases} 2 x + y = 4 \\ - x + y = 1 \end{cases}$

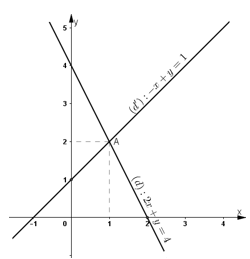
Ta biểu diễn hai đường thẳng (d): 2x + y = 4 và (d’): -x + y = 1 trên mặt phẳng tọa độ.

+ Xét (d): 2x + y = 4 hay (d): y = -2x + 4

Chọn x = 0 ⇒ y = 4

Chọn y = 0 ⇒ x = 2.

⇒ (d) đi qua hai điểm (0; 4) và (2; 0).

+ Xét (d’) : -x + y = 1 hay (d’) : y = x + 1.

Chọn x = 0 ⇒ y = 1

Chọn y = 0 ⇒ x = -1.

⇒ (d’) đi qua hai điểm (0; 1) và (-1; 0).

Nhận thấy (d) và (d’) cắt nhau tại A (1; 2).

Thử lại , thay x =1, y=2 vào các phương trình của hệ (II) ta được:

$\{\begin{cases} 2.1 + 2 = 4 \\ - 1 + 2 = 1 \end{cases} \Leftrightarrow \{\begin{cases} 4 = 4 \\ 1 = 1 \end{cases}$ (luôn đúng)

Vậy hệ phương trình (II) có đúng một nghiệm là (1; 2).

Câu 6:

Bạn Nga nhận xét: Hai hệ phương trình bậc nhất hai ẩn vô nghiệm thì luôn tương đương với nhau.

Bạn Phương khẳng định: Hai hệ phương trình bậc nhất hai ẩn cùng có vô số nghiệm thì cũng luôn tương đương với nhau.

Theo em, các ý kiến đó đúng hay sai? Vì sao? (Có thể cho một ví dụ hoặc minh họa bằng đồ thị).

Xem đáp án

- Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng ∅.

- Bạn Phương nhận xét sai.

Ví dụ: Xét hai hệ $\{\begin{cases} x - y = 0 \\ 2 x - 2 y = 0 \end{cases}$ và $\{\begin{cases} x + y = 0 \\ 3 x + 3 y = 0 \end{cases}$

Hệ $\{\begin{cases} x - y = 0 \\ 2 x - 2 y = 0 \end{cases}$ có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.

Hệ $\{\begin{cases} x + y = 0 \\ 3 x + 3 y = 0 \end{cases}$ có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.

Nhận thấy, tập nghiệm của hai hệ (I) và hệ (II) được biểu diễn bởi hai đường thẳng khác nhau nên hai hệ không tương đương.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Toán 9 Chương 3: Hệ hai phương trình bậc nhất hai ẩn

Bài 2: Hệ hai phương trình bậc nhất hai ẩn

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương