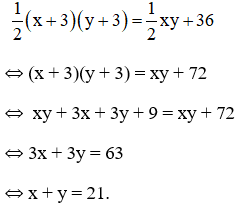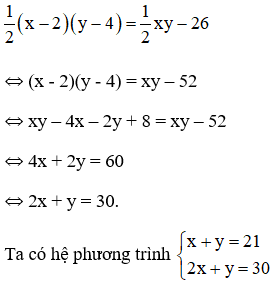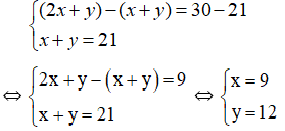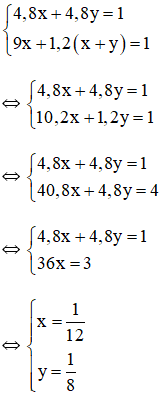4 câu hỏi trắc nghiệm thuộc Bài 6: Giải bài toán bằng cách lập hệ phương trình (Tiếp theo)

Câu 1:

Giải hệ phương trình (II) bằng cách đặt ẩn phụ (u = $\frac{1}{x}$ ; v = $\frac{1}{y}$ ) rồi trả lời bài toán đã cho.

$(I I I) \{\begin{cases} \frac{1}{x} = \frac{3}{2} . \frac{1}{y} \\ \frac{1}{x} + \frac{1}{y} = \frac{1}{24} \end{cases}$

Hãy giải bài toán trên bằng cách khác (gọi x là số phần công việc làm trong một ngày của đội A; y là số phần công việc làm trong một ngày của đội B). Em có nhận xét gì về cách giải này?

Xem đáp án

Đặt $\frac{1}{x}$ = u; $\frac{1}{y}$ = v,hệ (II)trở thành:

$\{\begin{array}{l} u = \frac{3}{2} v \\ u + v = \frac{1}{24} \end{array} \Leftrightarrow \{\begin{cases} u = \frac{3}{2} v \\ \frac{3}{2} v + v = \frac{1}{24} \end{cases} \Leftrightarrow \{\begin{cases} u = \frac{3}{2} v \\ \frac{5}{2} v = \frac{1}{24} \end{cases} \Leftrightarrow \{\begin{array}{l} u = \frac{3}{2} v \\ v = \frac{1}{60} \end{array} \Leftrightarrow \{\begin{cases} u = \frac{1}{40} \\ v = \frac{1}{60} \end{cases}$

Khi đó ta có:

$\{\begin{array}{l} \frac{1}{x} = \frac{1}{40} \\ \frac{1}{y} = \frac{1}{60} \end{array} \Leftrightarrow \{\begin{cases} x = 40 \\ y = 60 \end{cases}$

Vậy số ngày để đội A làm 1 mình xong đoạn đường đó là 40 ngày

Số ngày để đội B làm 1 mình xong đoạn đường đó là 60 ngày.

Cách khác:

Gọi x là số phần công việc làm trong 1 ngày của đội A

y là số phần công việc làm trong 1 ngày của đội B

Một ngày cả hai đội làm được $\frac{1}{24}$ công việc nên ta có phương trình: x + y = $\frac{1}{24}$

Mỗi ngày phần việc của đội A gấp rưỡi đội B nên ta có phương trình: x = $\frac{3}{2}$ y

Do đó, ta có hệ phương trình

$\{\begin{cases} x + y = \frac{1}{24} \\ x = \frac{3}{2} y \end{cases} \Leftrightarrow \{\begin{cases} \frac{3}{2} y + y = \frac{1}{24} \\ x = \frac{3}{2} y \end{cases} \Leftrightarrow \{\begin{cases} \frac{5}{2} y = \frac{1}{24} \\ x = \frac{3}{2} y \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{1}{60} \\ x = \frac{3}{2} y \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{1}{60} \\ x = \frac{1}{40} \end{cases}$

Trong 1 ngày, đội A làm được 1/40 công việc nên đội A làm 1 minh sẽ hoàn thành công việc trong 40 ngày

Trong 1 ngày, đội B làm được 1/60 công việc nên đội A làm 1 minh sẽ hoàn thành công việc trong 60 ngày

Nhận xét: Ở cách giải này thì chúng ta không cần đặt ẩn phụ để giải hệ phương trình.

Câu 2:

Tính độ dài hai cạnh góc vuông của một tam giác vuông, biết rằng nếu tăng mỗi cạnh lên 3cm thì diện tích tam giác đó sẽ tăng thêm 36 cm2, và nếu một cạnh giảm đi 2cm, cạnh kia giảm 4cm thì diện tích của tam giác giảm đi 26 cm2.

Xem đáp án

Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).

Diện tích tam giác ban đầu là $\frac{1}{2} x y$ (cm2)

+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)

Diện tích tam giác mới là: $\frac{1}{2} (x + 3) (y + 3)$ (cm2)

Diện tích tăng thêm 36cm2 nên ta có phương trình:

+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).

Diện tích tam giác mới là: $\frac{1}{2} (x - 2) (y - 2)$ (cm2).

Diện tích giảm đi 26cm2 nên ta có phương trình:

Lấy phương trình thứ hai trừ phương trình thứ nhất ta được:

Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm.

Câu 3:

Hai vòi nước cùng chảy vào một bể nước cạn (không có nước) thì sau $4 \frac{4}{5}$ giờ đầy bể. Nếu lúc đầu chỉ mở vòi thứ nhất và 9 giờ sau mới mở thêm vòi thứ hai thì sau $\frac{6}{5}$ giờ nữa mới đầy bể. Hỏi nếu ngay từ đầu chỉ mở vòi thứ hai thì sau bao lâu mới đầy bể?

Xem đáp án

Đổi $4 \frac{4}{5} = \frac{4.5 + 4}{5} = \frac{24}{5}$

Cách 1.

Gọi thời gian để vòi thứ nhất, vòi thứ 2 chảy 1 mình đầy bể là x (h), y (h). $x > \frac{24}{5}; y > \frac{24}{5}$

+ Một giờ vòi thứ nhất chảy được : $\frac{1}{x}$ ( bể )

Một giờ vòi thứ hai chảy được : $\frac{1}{y}$ ( bể )

+ Hai vòi nước cùng chảy vào một bể nước cạn (không có nước) thì sau $4 \frac{4}{5} = \frac{24}{5}$ giờ đầy bể.

=> Một giờ cả hai vòi chảy được: $1 : \frac{24}{5} = \frac{5}{24} (b ể) \Rightarrow \frac{1}{x} + \frac{1}{y} = \frac{5}{24}$

* Nếu ban đầu mở vòi 1 và 9 giờ sau mở thêm vòi 2 thì sau $\frac{6}{5}$ (h) đầy bể. Khi đó, thời gian vòi 1 chảy là: $9 + \frac{6}{5} = \frac{51}{5} (h) .$

Thời gian vòi 2 chảy là $\frac{6}{5}$ (h) $\Rightarrow \frac{51}{5} . \frac{1}{x} + \frac{6}{5} . \frac{1}{y} = 1$

$\Leftrightarrow \frac{51}{5 x} + \frac{6}{5 y} = 1 \Leftrightarrow \frac{51}{x} + \frac{6}{y} = 5$

Từ đó, ta có hệ phương trình: $\{\begin{cases} \frac{1}{x} + \frac{1}{y} = \frac{5}{24} \\ \frac{51}{x} + \frac{6}{y} = 5 \end{cases}$

Đặt $u = \frac{1}{x}; v = \frac{1}{y}$ khi đó hệ phương trình trên trở thành:

$\{\begin{array}{l} u + v = \frac{5}{24} \\ 51 u + 6 v = 5 \end{array} \Leftrightarrow \{\begin{cases} 6 u + 6 v = \frac{5}{4} \\ 51 u + 6 v = 5 \end{cases} \Leftrightarrow \{\begin{cases} - 45 u = \frac{- 15}{4} \\ u + v = \frac{5}{24} \end{cases} \Leftrightarrow \{\begin{array}{l} u = \frac{1}{12} \\ v = \frac{1}{8} \end{array} \Rightarrow \{\begin{array}{l} \frac{1}{x} = \frac{1}{12} \\ \frac{1}{y} = \frac{1}{8} \end{array} \Leftrightarrow \{\begin{array}{l} x = 12 \\ y = 8 \end{array} (t m đ k)$

Vậy nếu ngay từ đầu chỉ mở vòi 2 thì sau 8 giờ sẽ đầy bể.

Cách 2.

Gọi lượng nước vòi thứ nhất và vòi thứ hai chảy một mình trong 1 giờ lần lượt là x (bể) và y (bể).

Điều kiện 0 < x, y < 1.

+ Cả hai vòi cùng chảy trong $4 \frac{4}{5} = 4, 8$ giờ đầy 1 bể nên ta có phương trình: 4,8x + 4,8y = 1.

+ Nếu mở vòi thứ nhất trong 9 giờ thì chảy được 9x (bể)

$\frac{6}{5} = 1, 2$ giờ sau mở thêm vòi thứ hai thì chảy thêm được: 1,2 (x + y) (bể)

Khi đó bể đầy nên ta có phương trình: 9x + 1,2(x + y) = 1.

Ta có hệ phương trình:

⇒ một giờ vòi hai chảy một mình được $\frac{1}{8}$ bể

Vậy nếu ngay từ đầu chỉ mở vòi thứ hai thì sau 8 giờ sẽ đầy bể.

Câu 4:

Hai người thợ cùng làm một công việc trong 16 giờ thì xong. Nếu người thứ nhất làm 3 giờ và người thứ hai làm 6 giờ thì chỉ hoàn thành được 25% công việc. Hỏi nếu làm riêng thì mỗi người hoàn thành công việc đó trong bao lâu?

Xem đáp án

Gọi thời gian để người thứ nhất và người thứ hai một mình hoàn thành công việc lần lượt là x (giờ) và y (giờ). (Điều kiện x, y > 16).

⇒ Trong một giờ, người thứ nhất làm được $\frac{1}{x}$ (công việc); người thứ hai làm được $\frac{1}{y}$ (công việc).

+ Cả hai người cùng làm sẽ hoàn thành công việc trong 16 giờ nên ta có phương trình: $16 (\frac{1}{x} + \frac{1}{y}) = 1$

+ Người thứ nhất làm trong 3 giờ, người thứ hai làm trong 6 giờ thì hoàn thành $25 % = \frac{1}{4}$ công việc nên ta có phương trình: $3 . \frac{1}{x} + 6 . \frac{1}{y} = \frac{1}{4}$

Vậy ta có hệ phương trình: $\{\begin{cases} 16 . \frac{1}{x} + 16 . \frac{1}{y} = 1 \\ 3 . \frac{1}{x} + 6 . \frac{1}{y} = \frac{1}{4} \end{cases}$

Đặt $u = \frac{1}{x}; v = \frac{1}{y}$ , hệ phương trình trở thành:

$\{\begin{array}{l} 16 u + 16 v = 1 \\ 3 u + 6 v = \frac{1}{4} \end{array} \Leftrightarrow \{\begin{cases} u + v = \frac{1}{16} \\ u + 2 v = \frac{1}{12} \end{cases} \Leftrightarrow \{\begin{cases} u + 2 v - (u + v) = \frac{1}{12} - \frac{1}{16} \\ u + v = \frac{1}{16} \end{cases} \Leftrightarrow \{\begin{cases} v = \frac{1}{48} \\ u = \frac{1}{24} \end{cases}$

+ $u = \frac{1}{24} \Rightarrow \frac{1}{x} = \frac{1}{24} \Rightarrow x = 24 (t m đ k)$

+ $v = \frac{1}{48} \Rightarrow \frac{1}{y} = \frac{1}{48} \Rightarrow y = 48 (t m đ k)$

Vậy nếu làm riêng, người thứ nhất hoàn thành công việc sau 24 giờ và người thứ hai hoàn thành công việc trong 48 giờ.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Toán 9 Chương 3: Hệ hai phương trình bậc nhất hai ẩn

Bài 6: Giải bài toán bằng cách lập hệ phương trình (Tiếp theo)

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương