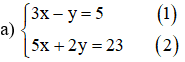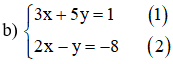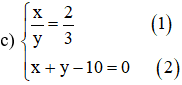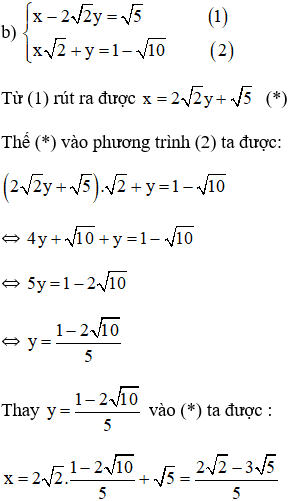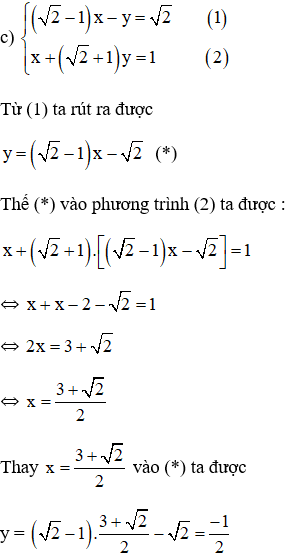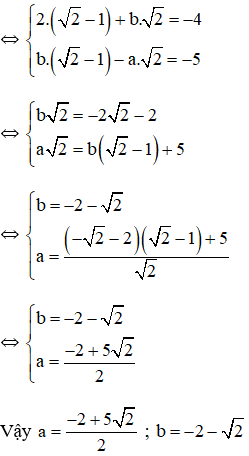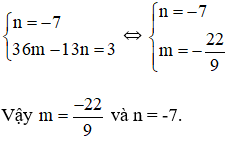5 câu hỏi trắc nghiệm thuộc Luyện tập trang 15-16 (Tập 2)

Giải SGK Toán 9 Chương 3: Hệ hai phương trình bậc nhất hai ẩn

Luyện tập trang 15-16 (Tập 2)

2498 lượt thi
5 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giải hệ phương trình $\{\begin{cases} x + 3 y = 1 \\ (a^{2} + 1) x + 6 y = 2 a \end{cases}$ trong mỗi trường hợp sau:

a) a = -1; b) a = 0; c) a = 1.

Xem đáp án

Cách 1

Ta có: $\{\begin{cases} x + 3 y = 1 & (1) \\ (a^{2} + 1) x + 6 y = 2 a & (2) \end{cases}$

Từ (1) rút ra được x = 1 – 3y (*)

Thay vào phương trình (2) ta được :

( $a^{2}$ + 1).(1 – 3y) + 6y = 2a

⇔ $a^{2}$ + 1 – 3( $a^{2}$ + 1)y + 6y = 2a

⇔ $a^{2}$ + 1- 2a = 3 $a^{2}$ .y – 6y + 3y

⇔ ( a - 1)2 = 3 $a^{2}$ y – 3y

⇔ 3( $a^{2}$ – 1).y = (a – 1)2 (**)

a) a = -1, phương trình (**) trở thành : 0y = 4

Phương trình trên vô nghiệm

Vậy hệ phương trình khi a = -1 vô nghiệm.

b) a = 0, phương trình (**) trở thành -3y = 1 ⇔ $y = \frac{- 1}{3}$

Thay $y = \frac{- 1}{3}$ vào (*) ta được x = 2.

Vậy hệ phương trình khi a = 0 có nghiệm duy nhất $(2; \frac{- 1}{3})$ .

c) a = 1, phương trình (**) trở thành: 0y = 0

Phương trình nghiệm đúng với mọi y.

Vậy hệ phương trình khi a = 1 có vô số nghiệm dạng (1 – 3y; y), (y ∈ R).

Cách 2:

a) Thay a = -1 vào hệ phương trình ta được hệ phương trình mới:

(I) $\{\begin{cases} x + 3 y = 1 \\ 2 x + 6 y = - 2 \end{cases}$

Ta có (biểu diễn x theo y từ phương trình thứ nhất):

$(I) \Leftrightarrow \{\begin{cases} x = - 3 y + 1 \\ 2 (- 3 y + 1) + 6 y = - 2 \end{cases} \Leftrightarrow \{\begin{cases} x = - 3 y + 1 \\ - 6 y + 2 + 6 y = - 2 \end{cases} \Leftrightarrow \{\begin{cases} x = - 3 y + 1 \\ 0 . y = - 4 (v ô l ý) \end{cases}$

Vậy hệ phương trình vô nghiệm khi a = - 1.

b) Thay a = 0 vào hệ phương trình ta được hệ phương trình mới:

(II) $\{\begin{cases} x + 3 y = 1 \\ x + 6 y = 0 \end{cases}$

Ta có (biểu diễn x theo y từ phương trình thứ hai):

$(I I) \Leftrightarrow \{\begin{array}{l} x + 3 y = 1 \\ x = - 6 y \end{array} \Leftrightarrow \{\begin{cases} - 6 y + 3 y = 1 \\ x = - 6 y \end{cases} \Leftrightarrow \{\begin{cases} - 3 y = 1 \\ x = - 6 y \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{- 1}{3} \\ x = 2 \end{cases}$

Vậy với a = 0 hệ phương trình có nghiệm duy nhất $(2; \frac{- 1}{3})$ .

c) Thay a=1 vào hệ phương trình ta được hệ phương trình mới:

(III) $\{\begin{cases} x + 3 y = 1 \\ 2 x + 6 y = 2 \end{cases}$

Ta có (biểu diễn x theo y từ phương trình thứ nhất):

$(I I I) \Leftrightarrow \{\begin{cases} x = - 3 y + 1 \\ 2 (- 3 y + 1) + 6 y = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = - 3 y + 1 \\ - 6 y + 2 + 6 y = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = - 3 y + 1 \\ 0 . y = 0 (l u ô n đ ú n g) \end{cases}$

Vậy với a= 1 hệ phương trình có vô số nghiệm với nghiệm tổng quát là (-3y + 1; y), (y ∈ R).

Câu 2:

Giải các hệ phương trình sau bằng phương pháp thế:

a) $\{\begin{cases} 3 x - y = 5 \\ 5 x + 2 y = 23 \end{cases}$ ;

b) $\{\begin{cases} 3 x + 5 y = 1 \\ 2 x - y = - 8 \end{cases}$ ;

c) $\{\begin{cases} \frac{x}{y} = \frac{2}{3} \\ x + y - 10 = 0 \end{cases}$

Xem đáp án

Cách 1:

Từ (1) ta rút ra được y = 3x – 5 (*)

Thế (*) vào phương trình (2) ta được :

5x + 2(3x – 5) = 23 ⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔ x = 3.

Thay x = 3 vào (*) ta được y = 3.3 – 5 = 4.

Vậy hệ phương trình có nghiệm duy nhất (3 ; 4).

Từ (2) ta rút ra được y = 2x + 8 (*)

Thế (*) vào phương trình (1) ta được :

3x + 5(2x + 8) = 1 ⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39 ⇔ x = -3.

Thay x = - 3 vào (*) ta được y = 2.(-3) + 8 = 2.

Vậy hệ phương trình có nghiệm duy nhất (-3 ; 2).

Từ (1) ta rút ra được $x = \frac{2}{3} y$ (*)

Thế (*) vào phương trình (2) ta được :

$\frac{2}{3} y + y - 10 = 0 \Leftrightarrow \frac{5}{3} y = 10 \Leftrightarrow y = 6$

Thay y = 6 vào (*) ta được x = 4.

Vậy hệ phương trình có nghiệm duy nhất (x ; y) = (4 ; 6).

Cách 2:

$a) \{\begin{cases} 3 x - y = 5 \\ 5 x + 2 y = 23 \end{cases} \Leftrightarrow \{\begin{cases} y = 3 x - 5 \\ 5 x + 2 (3 x - 5) = 23 \end{cases} \Leftrightarrow \{\begin{cases} y = 3 x - 5 \\ 5 x + 6 x - 10 = 23 \end{cases} \Leftrightarrow \{\begin{array}{l} y = 3 x - 5 \\ 11 x = 33 \end{array} \Leftrightarrow \{\begin{cases} y = 4 \\ x = 3 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất (3;4)

$b) \{\begin{cases} 3 x + 5 y = 1 \\ 2 x - y = - 8 \end{cases} \Leftrightarrow \{\begin{cases} 3 x + 5 y = 1 \\ y = 2 x + 8 \end{cases} \Leftrightarrow \{\begin{cases} 3 x + 5 (2 x + 8) = 1 \\ y = 2 x + 8 \end{cases} \Leftrightarrow \{\begin{cases} 3 x + 10 x + 40 = 1 \\ y = 2 x + 8 \end{cases} \Leftrightarrow \{\begin{array}{l} 13 x = - 39 \\ y = 2 x + 8 \end{array} \Leftrightarrow \{\begin{cases} x = - 3 \\ y = 2 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất (-3;2).

$c) \{\begin{cases} \frac{x}{y} = \frac{2}{3} \\ x + y - 10 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{2}{3} y \\ \frac{2}{3} y + y = 10 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{2}{3} y \\ \frac{5}{3} y = 10 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{2}{3} y \\ y = 6 \end{cases} \Leftrightarrow \{\begin{cases} x = 4 \\ y = 6 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất là (4;6).

Câu 3:

Giải các hệ phương trình sau bằng phương pháp thế:

a) $\{\begin{cases} x \sqrt{2} - y \sqrt{3} = 1 \\ x + y \sqrt{3} = \sqrt{2} \end{cases}$ ;

b) $\{\begin{cases} x - 2 \sqrt{2} y = \sqrt{5} \\ x \sqrt{2} + y = 1 - \sqrt{10} \end{cases}$ ;

c) $\{\begin{cases} (\sqrt{2} - 1) x - y = \sqrt{2} \\ x + (\sqrt{2} + 1) y = 1 \end{cases}$ .

Xem đáp án

Cách 1

a) $\{\begin{cases} x \sqrt{2} - y \sqrt{3} = 1 (1) \\ x + y \sqrt{3} = \sqrt{2} (2) \end{cases}$

Từ (2) suy ra x = $- y \sqrt{3} + \sqrt{2}$ (*)

Thế (*) vào (1) ta được:

$\begin{array}{l} (- y \sqrt{3} + \sqrt{2}) . \sqrt{2} - y \sqrt{3} = 1 \\ \Leftrightarrow y \sqrt{6} + 2 - y \sqrt{3} = 1 \\ \Leftrightarrow - y (\sqrt{6} + \sqrt{3}) = - 1 \\ \Leftrightarrow y = \frac{1}{\sqrt{6} + \sqrt{3}} \\ \Leftrightarrow y = \frac{\sqrt{6} - \sqrt{3}}{3} \end{array}$

Thay $\begin{array}{l} y = \frac{\sqrt{6} - \sqrt{3}}{3} \end{array}$ vào (*) ta được:

$\begin{array}{l} x = - \frac{\sqrt{6} - \sqrt{3}}{3} \end{array} . \sqrt{3} + \sqrt{2} = 1$

Vậy hệ phương trình có nghiệm duy nhất $(1; \frac{\sqrt{6} - \sqrt{3}}{3})$ .

Vậy hệ phương trình có nghiệm duy nhất $(\frac{2 \sqrt{2} - 3 \sqrt{5}}{5}; \frac{1 - 2 \sqrt{10}}{5})$ .

Vậy hệ phương trình có nghiệm duy nhất $(\frac{3 + \sqrt{2}}{2}; \frac{- 1}{2})$ .

Cách 2

$a) \{\begin{cases} x \sqrt{2} - y \sqrt{3} = 1 \\ x + y \sqrt{3} = \sqrt{2} \end{cases} \Leftrightarrow \{\begin{cases} x \sqrt{2} - y \sqrt{3} = 1 \\ x = - y \sqrt{3} + 2 \end{cases} \Leftrightarrow \{\begin{cases} (- y \sqrt{3} + 2) \sqrt{2} - y \sqrt{3} = 1 \\ x \sqrt{2} - y \sqrt{3} = 1 \end{cases} \Leftrightarrow \{\begin{cases} - y \sqrt{6} + 2 - y \sqrt{3} = 1 \\ x = - y \sqrt{3} + 2 \end{cases} \Leftrightarrow \{\begin{cases} - y (\sqrt{6} + \sqrt{3}) = - 1 \\ x = - y \sqrt{3} + 2 \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{1}{\sqrt{6} + \sqrt{3}} \\ x = - y \sqrt{3} + 2 \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{\sqrt{6} - \sqrt{3}}{3} \\ x = - \frac{\sqrt{6} - \sqrt{3}}{3} . \sqrt{3} + \sqrt{2} \end{cases} \Leftrightarrow \{\begin{array}{l} y = \frac{\sqrt{6} - \sqrt{3}}{3} \\ x = - (\sqrt{2} - 1) + \sqrt{2} \end{array} \Leftrightarrow \{\begin{cases} y = \frac{\sqrt{6} - \sqrt{3}}{3} \\ x = 1 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất $(1; \frac{\sqrt{6} - \sqrt{3}}{3})$

$b) \{\begin{cases} x - 2 \sqrt{2} y = \sqrt{5} \\ x \sqrt{2} + y = 1 - \sqrt{10} \end{cases} \Leftrightarrow \{\begin{array}{l} x = 2 \sqrt{2} y + 5 \\ (2 \sqrt{2} y + 5) \sqrt{2} + y = 1 - \sqrt{10} \end{array} \Leftrightarrow \{\begin{cases} x = 2 \sqrt{2} y + 5 \\ 4 y + \sqrt{10} + y = 1 - 10 \end{cases} \Leftrightarrow \{\begin{array}{l} x = 2 \sqrt{2} y + 5 \\ 5 y = 1 - 2 \sqrt{10} \end{array} \Leftrightarrow \{\begin{cases} x = 2 \sqrt{2} y + 5 \\ y = \frac{1 - 2 \sqrt{10}}{5} \end{cases} \Leftrightarrow \{\begin{array}{l} x = 2 \sqrt{2} . \frac{1 - 2 \sqrt{10}}{5} + \sqrt{5} \\ y = \frac{1 - 2 \sqrt{10}}{5} \end{array} \Leftrightarrow \{\begin{cases} x = \frac{2 \sqrt{2} - 3 \sqrt{5}}{5} \\ y = \frac{1 - 2 \sqrt{10}}{5} \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất $(\frac{2 \sqrt{2} - 3 \sqrt{5}}{5}; \frac{1 - 2 \sqrt{10}}{5})$ .

$c) \{\begin{cases} (\sqrt{2} - 1) x - y = \sqrt{2} \\ x + (\sqrt{2} + 1) y = 1 \end{cases} \Leftrightarrow \{\begin{cases} y = (\sqrt{2} - 1) x - \sqrt{2} \\ x + (\sqrt{2} + 1) [(\sqrt{2} - 1) x - \sqrt{2}] = 1 \end{cases} \Leftrightarrow \{\begin{cases} y = (\sqrt{2} - 1) x - \sqrt{2} \\ x + (\sqrt{2} + 1) (\sqrt{2} - 1) x - (\sqrt{2} + 1) . \sqrt{2} = 1 \end{cases} \Leftrightarrow \{\begin{cases} y = (\sqrt{2} - 1) x - \sqrt{2} \\ x + x - 2 - \sqrt{2} = 1 \end{cases} \Leftrightarrow \{\begin{cases} y = (\sqrt{2} - 1) x - \sqrt{2} \\ 2 x = 3 + \sqrt{2} \end{cases} \Leftrightarrow \{\begin{cases} y = (\sqrt{2} - 1) x - \sqrt{2} \\ x = \frac{3 + \sqrt{2}}{2} \end{cases} \Leftrightarrow \{\begin{cases} y = (\sqrt{2} - 1) . \frac{3 + \sqrt{2}}{2} - \sqrt{2} \\ x = \frac{3 + \sqrt{2}}{2} \end{cases} \Leftrightarrow \{\begin{cases} y = \frac{- 1}{2} \\ x = \frac{3 + \sqrt{2}}{2} \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất là $(\frac{3 + \sqrt{2}}{2}; \frac{- 1}{2})$ .

Câu 4:

a) Xác định các hệ số a và b, biết rằng hệ phương trình $\{\begin{cases} 2 x + b y = - 4 \\ b x - a y = - 5 \end{cases}$ có nghiệm (1; -2).

b) Cũng hỏi như vậy nếu phương trình có nghiệm là $\sqrt{2} - 1; \sqrt{2}$ .

Xem đáp án

a) Hệ phương trình $\{\begin{cases} 2 x + b y = - 4 \\ b x - a y = - 5 \end{cases}$ có nghiệm (1 ; -2) khi và chỉ khi (1;-2) thỏa mãn hệ phương trình.

Thay x = 1, y = -2 vào hệ phương trình ta được:

$\{\begin{cases} 2.1 + b . (- 2) = - 4 \\ b . 1 - a . (- 2) = - 5 \end{cases} \Leftrightarrow \{\begin{cases} 2 - 2 b = - 4 \\ b + 2 a = - 5 \end{cases} \Leftrightarrow \{\begin{array}{l} - 2 b = - 6 \\ 2 a = - b - 5 \end{array} \Leftrightarrow \{\begin{array}{l} b = 3 \\ a = - \frac{b + 5}{2} \end{array} \Leftrightarrow \{\begin{cases} b = 3 \\ a = - 4 \end{cases}$

Vậy với a = -4 và b = 3 thì hệ phương trình nhận (1; -2) là nghiệm.

b) Hệ phương trình $\{\begin{cases} 2 x + b y = - 4 \\ b x - a y = - 5 \end{cases}$ có nghiệm ( $\sqrt{2} - 1; \sqrt{2}$ ) khi và chỉ khi ( $\sqrt{2} - 1; \sqrt{2}$ ) thỏa mãn hệ phương trình.

Thay $(\sqrt{2} - 1; \sqrt{2})$ vào hệ phương trình ta được:

Câu 5:

Biết rằng: Đa thức P(x) chia hết cho đa thức x – a khi và chỉ khi P(a) = 0. Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x – 3: P(x) = mx3 + (m – 2)x2 – (3n – 5)x – 4n.

Xem đáp án

+ P(x) chia hết cho x + 1

⇔ P(-1) = 0

⇔ m.(-1)3 + (m – 2)(-1)2 – (3n – 5).(-1) – 4n = 0

⇔ -m + m – 2 + 3n – 5 – 4n = 0

⇔ -n – 7 = 0

⇔ n = -7 (1)

+ P(x) chia hết cho x – 3

⇔ P(3) = 0

⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0

⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0

⇔ 36m – 13n = 3 (2)

Từ (1) và (2) ta có hệ phương trình :

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Toán 9 Chương 3: Hệ hai phương trình bậc nhất hai ẩn

Luyện tập trang 15-16 (Tập 2)

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương