29 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2021 có đáp án (Phần 1) (Đề 13)

Câu 1:

y = - 3 x^{2}

có đồ thị là hình vẽ nào dưới đây

A. Media VietJack

B. Media VietJack

C.

Hàm số y = -3x^2 có đồ thị là hình vẽ nào dưới đây (ảnh 1)

D.

Hàm số y = -3x^2 có đồ thị là hình vẽ nào dưới đây (ảnh 2)

Xem đáp án

Đáp án đúng là B

Câu 2:

Hàm số nào dưới đây là hàm số bậc nhất ?

$A . y = \sqrt{x} + 10$

$B . y = - 4 x^{2}$

$C . y = \frac{2021}{x}$

$D . y = 20 x - 21$

Xem đáp án

Đáp án đúng là D

Câu 3:

Điều kiện của x để biểu thức $\sqrt{2 x + 10}$ có nghĩa là :

A. $x \leq 5$

B. $x \geq - 5$

C. $x \geq 5$

D. $x \leq - 5$

Xem đáp án

Đáp án đúng là B

Câu 4:

Phương trình nào sau đây là phương trình bậc hai một ẩn ?

$A . x^{3} - 4 x + 6 = 0$

$B .3 x + 11 = 0$

$C .3 x^{2} - x + 5 = 0$

$D . x^{4} - 2 x^{2} + 9 = 0$

Xem đáp án

Đáp án đúng là C

Câu 5:

Cặp số (15;16) là nghiệm của hệ phương trình nào dưới đây ?

$A . \{\begin{cases} x + y = - 31 \\ 15 x - 16 y = 31 \end{cases}$

$B . \{\begin{cases} - x + y = 1 \\ 15 x + 16 y = 31 \end{cases}$

$C . \{\begin{cases} - x + y = - 1 \\ 15 x + 16 y = - 31 \end{cases}$

$D . \{\begin{cases} x + y = 31 \\ 15 x - 16 y = - 31 \end{cases}$

Xem đáp án

Đáp án đúng là D

Câu 6:

Cho tứ giác ABCD nội tiếp đường tròn (O) và $∠ B C D = 112 °$ . Số đo của $∠ B O D$ bằng:

Cho tứ giác ABCD nội tiếp đường tròn (O) và góc BCD = 112 độ . Số đo của góc BOD bằng: (ảnh 1)

A. $68 °$

B. $136 °$

C. $112 °$

D. $56 °$

Xem đáp án

Đáp án đúng là B

Câu 7:

Nghiệm của hệ phương trình $\{\begin{cases} 5 x - 3 y = - 5 \\ x - 2 y = - 8 \end{cases}$ là :

A. (-5 ; -2)

B. (-2; -5)

C. (5; 2)

D. (2; 5)

Xem đáp án

Đáp án đúng là D

Câu 8:

Cho hàm số y = ax + b có đô thị như hình vẽ bên dưới

Hàm số đã cho là :

A. y = -x + 4

B. y = x + 4

C. y = -x - 4

D. y = x- 4

Xem đáp án

Đáp án đúng là A

Câu 9:

Cho đường tròn tâm O bán kính 12 cm và điểm M nằm ngoài đường tròn sao cho MO = 20cm. Vẽ tiếp tuyến MA với đường tròn (O) (A là tiếp điểm). Độ dài của đoạn thẳng MA bằng :

A. 16cm

B. 20 cm

C. 256 cm

D. 8 cm

Xem đáp án

Đáp án đúng là A

Câu 10:

Một cột cờ cao 7,8 m có bóng trên mặt đất dài 13m. Số đo góc $α$ mà tia sáng mặt trời tạo với mặt đất (làm tròn đến độ) bằng

A. $31 °$

B. $59 °$

C. $37 °$

D. $53 °$

Xem đáp án

Đáp án đúng là A

Câu 11:

Gọi S và P lần lượt là tổng và tích hai nghiệm của phương trình $x^{2} - 4 x - 7 = 0$ . Giá trị của biểu thức S. P bằng :

A. -14

B. 14

C. -28

D. 28

Xem đáp án

Đáp án đúng là C

Câu 12:

Cho đường tròn tâm O bán kính 4 cm. Độ dài của đường tròn (O) bằng:

A. $8 πcm$

B. $16 πcm$

C. $2 πcm$

D. $4 πcm$

Xem đáp án

Đáp án đúng là A

Câu 13:

Thể tích của hình cầu có bán kính 15 cm bằng :

$A .13500 π (c m^{3})$

$B .900 π (c m^{3})$

$C .300 π (c m^{3})$

$D .4500 π (c m^{3})$

Xem đáp án

Đáp án đúng là D

Câu 14:

Tọa độ giao điểm của đường thẳng (d): y = -2x + 3 và parabol (P)

y = x^{2}

là

$A . (1; - 1); (3; - 9)$

$B . (- 1; - 1), (- 3; 9)$

$C . (1; 1), (- 3; 9)$

$D . (1; 1), (- 3; - 9)$

Xem đáp án

Đáp án đúng là C

Câu 15:

Giá trị của biểu thức $5 \sqrt{144} - \sqrt[3]{15625} + 7$ bằng:

A. 92

B. -72

C. 42

D. -56

Xem đáp án

Đáp án đúng là C

Câu 16:

Bạn Lan đi siêu thị mua hai loại trái cây là xoài và ổi. Số tiền mà Lan phải trả theo giá niêm yết khi mua 2kg xoài và 3kg ổi là 80 000 đồng. Tuy nhiên, khi Lan trả tiền thì giá của xoài được giảm 10%so với giá niêm yết. Do đó, Lan chỉ trả 75 000 đồng. Giá niêm yết của mỗi kg xoài và kg ổi lần lượt là

A. 10000 đồng và 25 000 đồng

B. 28000 đồng và 8 000 đồng

C. 16000 đồng và 16 000 đồng

D. 25000 đồng và 10 000 đồng

Xem đáp án

Đáp án đúng là D

Câu 17:

Cho đường thẳng $(d_{1}) : y = a x + b$ đi qua điểm M(0; 5) và đồng thời song song với đường thẳng $(d_{2}) : y = 2 x - \frac{3}{4}$ . Giá trị của a và b là :

$A . a = \frac{- 3}{4}, b = 2$

$B . a = 2, b = 5$

$C . a = 5, b = 2$

$D . a = 2, b = - \frac{3}{4}$

Xem đáp án

Đáp án đúng là B

Câu 18:

Tất cả giá trị của tham số m sao cho hệ phương trình $\{\begin{cases} x + (m - 3) y = 2 \\ x - 6 y = 4 \end{cases}$ có nghiệm duy nhất là :

$A . m \neq 9$

$B . m \neq - 3$

$C . m \neq 3$

$D . m \neq - 9$

Xem đáp án

Đáp án đúng là B

Câu 19:

Giá trị của tham số m sao cho phương trình $2 x^{2} + 4 x + m + 4 = 0$ có nghiệm kép là :

A. m = -2

B. m = 2

C. m = 6

D. m = -6

Xem đáp án

Đáp án đúng là A

Câu 20:

Một lon sữa hình trụ có đường kính đáy 1,2 dm và chiều cao 1,8 dm. Diện tích nhãn dán xung quanh (không kể mép dán) của lon sữa đó (kết quả làm tròn đến hai chữ số thập phân và lấy giá trị gần đúng của $π$ bằng 3,14) là :

$A .13,56 d m^{2}$

$B .2,16 d m^{2}$

$C .6,78 d m^{2}$

$D .4,07 d m^{2}$

Xem đáp án

Đáp án đúng là C

Câu 21:

Giải phương trình và hệ phương trình sau :

$a) x^{2} - 5 x + 6 = 0$

Xem đáp án

$a) x^{2} - 5 x + 6 = 0$

Ta có : $Δ = {(- 5)}^{2} - 4.6 = 1 > 0$ nên phương trình có hai nghiệm phân biệt

$[\begin{array}{l} x_{1} = \frac{5 + 1}{2} = 3 \\ x_{2} = \frac{5 - 1}{2} = 2 \end{array}$

Vậy tập nghiệm của phương trình $S = \{2; 3\}$

Câu 22:

Giải phương trình và hệ phương trình sau : $b) \{\begin{cases} x + 2 y = 21 \\ 3 x - y = 7 \end{cases}$

Xem đáp án

$b) \{\begin{cases} x + 2 y = 21 \\ 3 x - y = 7 \end{cases} \Leftrightarrow \{\begin{cases} x + 2 y = 21 \\ 6 x - 2 y = 14 \end{cases} \Leftrightarrow \{\begin{cases} 7 x = 35 \\ y = 3 x - 7 \end{cases} \Leftrightarrow \{\begin{cases} x = 5 \\ y = 8 \end{cases}$

Vậy hệ phương trình có nghiệm

(x; y) = (5; 8)

Câu 23:

Rút gọn biểu thức $A = \frac{\sqrt{15} - \sqrt{3}}{\sqrt{5} - 1} - \frac{1}{2 - \sqrt{3}}$

Xem đáp án

$\begin{array}{l} A = \frac{\sqrt{15} - \sqrt{3}}{\sqrt{5} - 1} - \frac{1}{2 - \sqrt{3}} = \frac{\sqrt{3} (\sqrt{5} - 1)}{\sqrt{5} - 1} - \frac{2 + \sqrt{3}}{(2 - \sqrt{3}) (2 + \sqrt{3})} \\ = \sqrt{3} - 2 - \sqrt{3} = - 2 \end{array}$

Vậy A = -2

Câu 24:

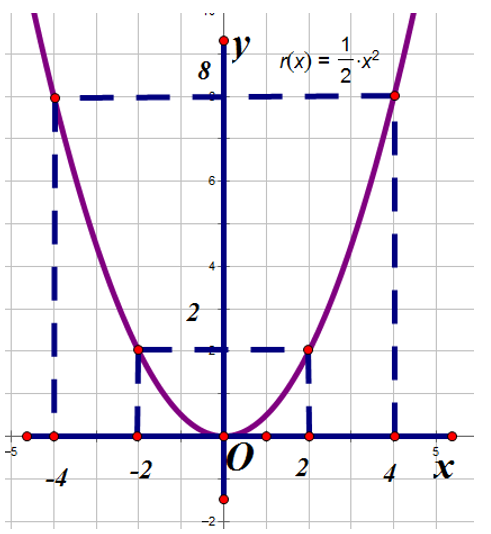
b) Vẽ đồ thị của hàm số $y = \frac{1}{2} x^{2}$

Xem đáp án

Parabol $(P) : y = \frac{1}{2} x^{2}$ có bề lõm hướng lên trên và nhận Oy làm trục đối xứng

Ta có bảng giá trị sau :

$\begin{array}{l} x - 4 - 2024 \\ y = \frac{1}{2} x^{2} 82028 \end{array}$

$\Rightarrow P a r a b o l (P) : y = \frac{1}{2} x^{2}$ đi qua các điểm $(- 4; 8), (- 2; 2), (0; 0), (2; 2), (4; 8)$

b) Vẽ đồ thị của hàm số y = 1/2 x^2 (ảnh 1)

Câu 25:

a) Tìm tất cả các giá trị của tham số m sao cho phương trình $x^{2} - m x - m - 1 = 0$ có hai nghiệm phân biệt $x_{1}; x_{2}$ thỏa mãn $\frac{1}{x_{1}} + \frac{1}{x_{2}} = x_{1} + x_{2}$

Xem đáp án

a) Phương trình $x^{2} - m x - m - 1 = 0$ có hai nghiệm phân biệt $x_{1}; x_{2}$

$\begin{array}{l} \Leftrightarrow Δ = b^{2} - 4 a c > 0 \Leftrightarrow {(- m)}^{2} - 4.1. (- m - 1) > 0 \\ \Leftrightarrow m^{2} + 4 m + 4 > 0 \Leftrightarrow {(m + 2)}^{2} > 0 \Leftrightarrow m \neq - 2 (1) \end{array}$

Khi đó, theo hệ thức Vi- et ta có : $\{\begin{cases} x_{1} + x_{2} = m \\ x_{1} x_{2} = - m - 1 \end{cases}$ . Theo bài ra ta có :

$\begin{array}{l} \frac{1}{x_{1}} + \frac{1}{x_{2}} = x_{1} + x_{2} \Leftrightarrow \frac{x_{1} + x_{2}}{x_{1} x_{2}} = x_{1} + x_{2} \\ \Leftrightarrow \frac{x_{1} + x_{2}}{x_{1} x_{2}} - x_{1} + x_{2} = 0 \Leftrightarrow (x_{1} + x_{2}) (\frac{1}{x_{1} x_{2}} - 1) = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x_{1} + x_{2} = 0 \\ x_{1} x_{2} = 1 \end{array} \Leftrightarrow [\begin{array}{l} m = 0 \\ - m - 1 = 1 \end{array} \Leftrightarrow [\begin{array}{l} m = 0 (t m) \\ m = - 2 (k t m) \end{array}$

Vậy m= 0 là giá trị cần tìm

Câu 26:

b) Trong năm học 2020-2021, trường Trung học cơ sở A tổ chức cho học sinh đăng ký tham gia câu lạc bộ Toán học và câu lạc bộ Sáng tạo khoa học. Ở học kỳ 1, số lượng học sinh tham gia câu lạc bộ Toán học ít hơn số lượng học sinh tham gia câu lạc bộ Sáng tạo khoa học là 50 học sinh. Sang học kỳ 2, có 5 học sinh chuyển từ câu lạc bộ Sáng tạo khoa học sang câu lạc bộ Toán học nên số lượng học sinh của câu lạc bộ Toán học bằng $\frac{3}{4}$ số lượng học sinh của câu lạc bộ Sáng tạo khoa học. Biết rằng trong năm học, tổng số học sinh tham gia cả hai câu lạc bộ không thay đổi và mỗi học sinh chỉ tham gia một câu lạc bộ. Hỏi số lượng học sinh của mỗi câu lạc bộ ở học kỳ 2 là bao nhiêu ?

Xem đáp án

b) Gọi số lượng học sinh tham gia câu lạc bộ Toán học ở học kỳ I là x học sinh $(x \in ℕ *)$

Vì số lượng học sinh tham gia câu lạc bộ Toán học ít hơn số lượng học sinh tham gia câu lạc bộ Sáng tạo khoa học là 50 học sinh nên số học sinh tham gia câu lạc bộ Sáng tạo khoa học ở học kỳ I là x + 50 (học sinh)

Học kỳ 2, số học sinh tham gia câu lạc bộ Sáng tạo khoa học và câu lạc bộ Toán học lần lượt là x + 50 - 5 = x + 45 (học sinh) và x + 5 (học sinh)

Do số lượng học sinh của câu lạc bộ Toán học bằng $\frac{3}{4}$ số lượng học sinh của câu lạc bộ Sáng tạo khoa học nên ta có phương trình

$x + 5 = \frac{3}{4} (x + 45) \Leftrightarrow x + 5 = \frac{3}{4} x + \frac{135}{4} \Leftrightarrow x = 115 (t m d k)$

Vậy học kỳ 2, số lượng học sinh tham gia câu lạc bộ Toán học là 115 + 5 = 120 học sinh, số lượng học sinh của câu lạc bộ Sáng tạo khoahọc115 + 45 = 160 học sinh

Câu 27:

Cho tam giác ABC ( $A B < A C$ ) có ba góc nhọn và nội tiếp đường tròn (O). Các đường cao AD, BE và CF của tam giác ABC cắt nhau tại điểm H

a) Chứng minh các tứ giác BCEF, EHDC nội tiếp

Xem đáp án

b)

+)Xét tứ giác BFEC có $∠ B F C = ∠ B E C = 90 ° (g t)$

Suy ra tứ giác BFEC nội tiếp (Tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau)

+)Xét tứ giác EHDC có $∠ H D C + ∠ H E C = 90 ° + 90 ° = 180 °$ suy ra HDCE là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng $180 °$

Câu 28:

b) Gọi K là giao điểm của hai đường thẳng EF và BC. Đường thẳng AK cắt đường tròn (O) tại điểm thứ hai là I. Chứng minh tam giác KBF đồng dạng với tam giác KEC và $K I . K A = K F . K E$

Xem đáp án

b) Ta có :

Tứ giác BFCE nội tiếp nên $∠ K F B = ∠ K C E$ (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp)

Xét $∆ K B F$ và $∆ K E C$ có : $\{\begin{cases} ∠ K F B = ∠ K C E (c m t) \\ ∠ B K F = ∠ C K E \end{cases} \Rightarrow Δ K B F ∽ Δ K E C (g . g)$

$\Rightarrow \frac{K B}{K E} = \frac{K F}{K C}$ (hai cặp cạnh tương ứng tỉ lệ) $\Rightarrow K F . K E = K B . K C (1)$

Trong (O) có $∠ K A B = ∠ K C I$ (hai góc nội tiếp cùng chắn cung BBI

Xét $∆ K A B$ và $∆ K C I$ có : $\{\begin{cases} ∠ A K B = ∠ C K I \\ ∠ K A B = ∠ K C I (c m t) \end{cases} \Rightarrow Δ K A B ∽ Δ K C I (g . g)$

$\Rightarrow \frac{K A}{K C} = \frac{K B}{K I}$ (hai cặp cạnh tương ứng tỉ lệ) $\Rightarrow K A . K I = K B . K C (2)$

Từ (1) và (2) suy ra $K I . K A = K E . K F$

Câu 29:

c) Qua điểm B vẽ đường thẳng song song với đường thẳng AC cắt các đường thẳng AK và AH lần lượt tại điểm M và điểm N. Chứng minh HM = HN.

Xem đáp án

c) Ta có : $K I . K A = K F . K E (c m t) \Rightarrow \frac{K I}{K E} = \frac{K F}{K A}$

Xét $∆ K I F$ và $∆ K E A$ ta có : $\frac{K I}{K E} = \frac{K F}{K A} (c m t); ∠ A K E$ chung

$\Rightarrow Δ K I F ∽ Δ K E A (c . g . c) \Rightarrow ∠ K I F = ∠ F E A$ (hai góc tương ứng)

$\Rightarrow A I F E$ là tứ giác nội tiếp (Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện) $\Rightarrow I, A, F, E$ cùng thuộc một đường tròn.

Mà tứ giác AEHF là tứ giác nội tiếp (do có $∠ A E H + ∠ A F H = 180 °) \Rightarrow A, E, H, F$ cùng thuộc một đường tròn

Do đó 5 điểm $I, A, F, H, E$ cùng nội tiếp đường tròn đường kính AH

$\Rightarrow ∠ H I A = 90 °$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow H I ⊥ A K \Rightarrow ∠ H I M = 90 °$ (kề bù với $∠ H I A)$

Ta có: $\{\begin{cases} B E ⊥ A C \\ A C / / M N (g t) \end{cases} \Rightarrow B E ⊥ M N$ (từ vuông góc đến song song) $\Rightarrow ∠ H B M = 90 °$

$\Rightarrow ∠ H I M = ∠ H B M = 90 ° \Rightarrow ∠ H I M + ∠ H B M = 180 °$

$\Rightarrow B H I M$ nội tiếp đường tròn đường kính HM (dấu hiệu nhận biết)

$\Rightarrow ∠ M H B = ∠ M I B = ∠ K I B$ (2 góc nội tiếp cùng chắn cung BBM

Mà $∠ K I B = ∠ K C A$ (vì $∠ K I B$ là góc ngoài tại đỉnh I của tứ giác nội tiếp BIAC)

$\Rightarrow ∠ M H B = ∠ K C A$

Mặt khác ta có : $∠ K C A = ∠ A H E$ (cùng phụ $∠ H A E)$ và $∠ A H E = ∠ B H N$ (đối đỉnh)

$\Rightarrow ∠ M H B = ∠ B H N \Rightarrow H B$ là tia phân giác của góc MMHN

$\Rightarrow Δ M H N$ cân tại H (do có HB là đường cao đồng thời là phân giác)

Vậy HM= HN

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2021 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2021 có đáp án (Phần 1) (Đề 13)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm