Bài tập Góc nội tiếp có đáp án
-
2237 lượt thi
-
22 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
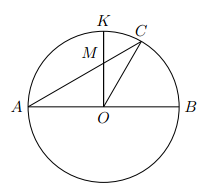
Muốn xác định tâm của một đường tròn mà chỉ dùng ê ke thì phải làm như thế nào?
 Xem đáp án
Xem đáp án
Để xác định tâm của một đường tròn mà chỉ dùng ê ke, ta thực hiện theo các bước sau:
Bước 1: Kẻ đường thẳng cắt đường tròn tại A và B.
Bước 2: Qua B, dùng ê ke kẻ đường thẳng vuông góc với AB ở B và cắt đường tròn tại C.
Bước 3: Nối C với A.
Bước 4: Qua A, dùng ê ke kẻ đường thẳng vuông góc với AB tại A và cắt đường tròn tại D.
Bước 5: Nối B với D. Giao điểm của AC và BD là tâm đường tròn.
Câu 2:
Dựng một tam giác vuông, biết cạnh huyền dài 4 cm và một cạnh góc vuông dài 2,5 cm.
 Xem đáp án
Xem đáp án
Giả sử dựng được tam giác ABC vuông có cạnh huyền BC = 4 cm, cạnh góc vuông AB = 2,5 cm.
Gọi O là trung điểm của BC. Ta có: OB = OC = OA = 2 cm.
Vậy tam giác ABC nội tiếp đường tròn đường kính BC có cạnh AB = 2,5 cm.
Cách dựng: Ta thực hiện các bước sau:
Bước 1: Dựng đường tròn bán kính r = 2 cm.
Bước 2: Qua O kẻ đường thẳng d cắt đường tròn tại hai điểm B cà C
Bước 3: Dựng đường tròn tâm B, bán kính 2,5 cm và cắt đường tròn (O) tại .
Vậy thỏa mãn đề bài.
Câu 4:
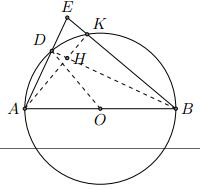
Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.
 Xem đáp án
Xem đáp án
Ta có là các góc nội tiếp chắn nửa đường tròn nên:
Do đó, là trực tâm của tam giác SAB.
Vậy ta được .
Câu 6:
Trên nửa đường tròn (O) đường kính AB, lấy điểm M (khác A và B). Vẽ tiếp tuyến của (O) tại A. Đường thẳng BM cắt tiếp tuyến đó tại C. Chứng minh rằng ta luôn có:
 Xem đáp án
Xem đáp án
Ta có (tính chất của hai tiếp tuyến)
Suy ra vuông tại A.
Mặt khác, (góc nội tiếp chắn nửa đường tròn) nên AM là đường cao của tam giác ABC.
Theo hệ thức lượng trong tam giác vuông, ta có .
Câu 9:
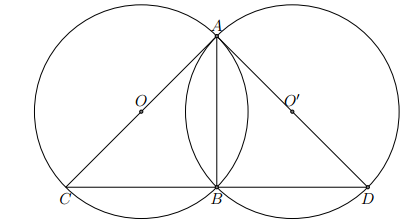
Cho đường tròn (O) và (O’) bằng nhau, cắt nhau tại A và B. Qua B vẽ một cát tuyến cắt đường tròn (O) và (O’) lần lượt tại C và D.
a) Chứng minh AC = AD.
b) Tìm quỹ tích trung điểm M của CD khi cát tuyến CBD quay quanh B.
 Xem đáp án
Xem đáp án
a) Từ giả thiết “hai đường tròn (O) và (O’) bằng nhau”, nên hai cung nhỏ AB của chúng bằng nhau, do đó:
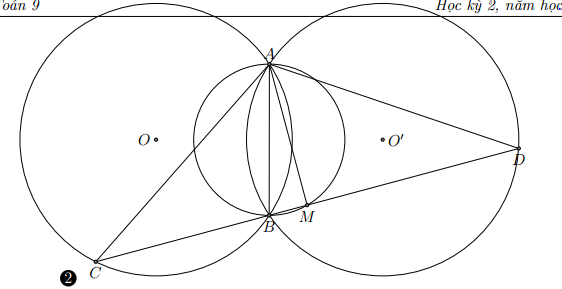
b) Ta lần lượt thực hiện:
Phân thuận: với M là trung điểm của CD, suy ra , vì cân tại A
Vậy điểm M thuộc đường tròn đường kính AB
Phần đảo: Lấy điểm và giả sử đường thẳng BM cắt (O) và (O’) theo thứ tự tại C và D, ta cần chứng minh M là trung điểm CD.
Thật vậy, trong cân tại A, ta có: . Góc nội tiếp chắn nửa đường tròn , vì tam giác cân đường cao là trung tuyến
Kết luận: quỹ tích các điểm M là đường tròn đường kính AB.
Câu 12:
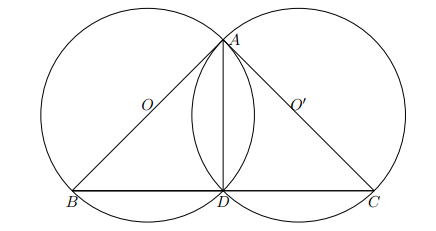
Cho hai đường tròn bằng nhau (O) và (O’) cắt nhau tại A và B. Vẽ đường thẳng qua A cắt (O) tại M và (O’) tại N (A nằm giữa M và N). Hỏi MBN là tam giác gì: Tại sao?
 Xem đáp án
Xem đáp án
Hai đường tròn (O) và (O’) bằng nhau nên AOBO’ là hình thoi.
Do đó . Theo tính chất của góc nội tiếp, ta có:
Vậy ta được là tam giác cân tại B.
Câu 16:
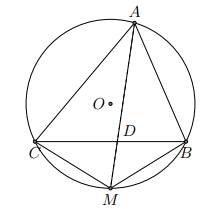
Cho nửa đường tròn đường kính AB. Gọi O là điểm chính giữa của nửa đường tròn và M là một điểm bất kì của nửa đường tròn đó. Tia AM cắt đường tròn (O; OA) tại điểm thứ hai là N. Chứng minh rằng MN = MB.
 Xem đáp án
Xem đáp án
Từ giả thiết ta có ngay , vì chúng đều là góc nội tiếp chắn nửa đường tròn đường kính AB.
Mặt khác, ta cũng có OA = OB => B
Do đó,
Khi đó, vuông tại M có nên nó là tam giác vuông cân, suy ra MN = NB
Câu 17:
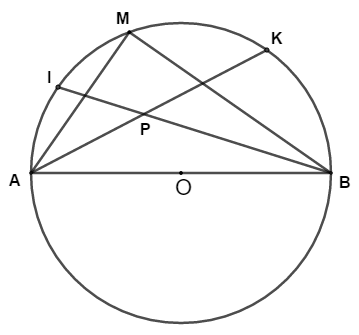
Cho đường tròn (O) và hai dây MA, MB vuông góc với nhau. Gọi I và K lần lượt là điểm chính giữa của các cung nhỏ MA và MB. Gọi P là giao điểm của AK và BI
a) Chứng minh ba điểm A, O, B thẳng hàng.
b) Chứng minh rằng P là tâm đường tròn nội tiếp của
c) Giả sử MA = 12 cm, MB = 16 cm, tính bán kính của đường tròn nội tiếp
 Xem đáp án
Xem đáp án
Vậy bán kính của đường tròn nội tiếp tam giác MAB bằng 4 cm.
Câu 18:
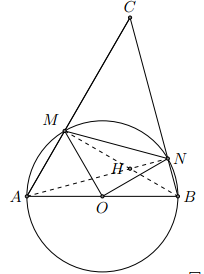
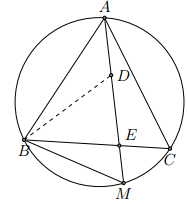
Cho đường tròn tâm O đường kính AB và một điểm C chạy trên một nửa đường tròn. Vẽ một đường tròn (I) tiếp xúc với đường tròn (O) tại C và tiếp xúc với đường kính AB tại D, đường tròn này cắt CA và CB tại các điểm thứ hai là M và N. Chứng minh rằng:
a) Ba điểm M, I, N thẳng hàng
b)
c) Đường thẳng CD đi qua điểm cố định
d) Nêu cách dựng đường tròn (I) nói trên.
 Xem đáp án
Xem đáp án
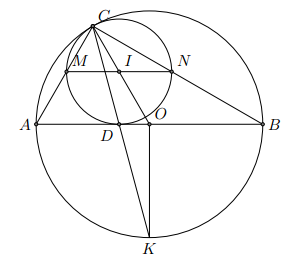
=> K là điểm chính giữa của cung.
Do đó K cố định. Vậy CD luôn đi qua điểm cố định K
d) Để dựng đường tròn (I), ta thực hiện:
- Dựng OK vuông góc với AB, với K thuộc nửa đường tròn không chứa điểm C.
- Nối CK cắt AB tại D.
- Dựng đường thẳng qua D vuông góc với AB cắt CD tại I.
- Dựng đường tròn (I; ID) đây chính là đường tròn cần dựng.
Câu 19:
Cho có ba góc nhọn nội tiếp đường tròn (O), đường cao AH. Kẻ đường kính AE.
a) Tính
b) Chứng minh rằng
c) Gọi K là giao điểm của AH với đường tròn (O). Tứ giác BCEK là hình gì?
 Xem đáp án
Xem đáp án
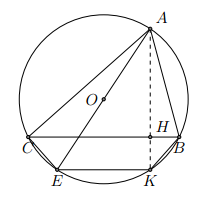
Từ (1) và (2) ta kết luận BCEK là hình thang cân.