Bài tập Đường tròn ngoại tiếp – đường tròn nội tiếp có đáp án
-
2241 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
a) Vẽ đường tròn tâm O, bán kính 2 cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) đó.
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b rồi vẽ đường tròn (O; r)
 Xem đáp án
Xem đáp án
a) Cách vẽ: mở compa một khoảng 2 cm. Quay một vòng để vẽ đường tròn (O;2)
b) Cách vẽ
- Từ điểm A bất kì trên đường tròn, vẽ đường kính AC.
- Vẽ đường kính BD vuông góc với đường kính AC
- A, B, C, D là bốn đỉnh của hình vuông cần dựng.

c) Đường tròn nội tiếp hình vuông có đường kính bằng cạnh của hình vuông ABCD.
Ta có
Cách vẽ đường tròn nội tiếp hình vuông. Kẻ , vẽ đường tròn (O;OE)
Câu 2:
a) Vẽ đều cạnh a = 3 cm.
b) Vẽ đường tròn (O; R) ngoại tiếp . Tính R.
c) Vẽ đường tròn (O; r) nội tiếp . Tính r.
d) Vẽ tam giác đều IJK ngoại tiếp đường tròn (O; R)
 Xem đáp án
Xem đáp án
a) Cách vẽ:
- Vẽ BC = 3 cm.
- Vẽ các đường tròn (B; 3 cm) và (C; 3 cm) cắt nhau tại A.
- là tam giác đều có cạnh bằng 3 cm.
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC trùng với trọng tâm của tam giác đó.
Ta có bán kính R của đường tròn ngoại tiếp là
Các đường tròn này cắt nhau tại I, J, K thì là tam giác ngoại tiếp đường tròn (O; R)
Câu 5:
Cho lục giác đều ABCDEF tâm O
a) Gọi a là độ dài cạnh lục giác đều. Tính bán kính đường tròn ngoại tiếp R và bán kính đường tròn nội tiếp r của lục giác.
b) Gọi m là một điểm bất kì trong tam giác AOB. Gọi H, I, K theo thứ tự là hình chiếu của M trên OA, OB, CF. chứng minh rằng năm điểm M, H, I, O, K cùng thuộc một đường tròn.
c) Chứng minh rằng tam giác HIK là tam giác đều.
 Xem đáp án
Xem đáp án
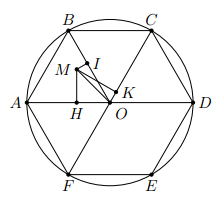
c) Giả sử K thuộc đoạn thẳng OF
Xét đường tròn đi qua năm điểm H, I, K, O, M ta có vì góc nội tiếp cùng chắn một cung.
Câu 6:
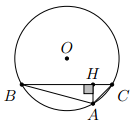
Trên một đường tròn bán kính R lần lượtđặt theo cùng một chiều, kẻ từ một điểm A, ba cung AB, BC, CD sao cho sđ , sđ và sđ
a) Tứ giác ABCD là hình gì?
b) Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.
c) Tính độ dài các cạnh của tứ giác ABCD theo R
 Xem đáp án
Xem đáp án
(vì có cặp góc so le trong bằng nhau)
Do đó, ABCD là hình thang và hình thang nội tiếp đường tròn nên nó là hình thang cân.
b) Gọi M là giao điểm của AC và BD, vì là góc có đỉnh ở bên trong đường tròn nên
Câu 8:
Một đa giác đều nội tiếp đường tròn (O; R). Biết độ dài mỗi cạnh của nó là . Hỏi đa giác đó là hình gì?
 Xem đáp án
Xem đáp án
Gọi a, n theo thứ tự là số đỉnh, độ dài cạnh của đa giác đều đó, ta có a =
Vậy đa giác cần tìm là tứ giác đều (hình vuông)
Câu 10:
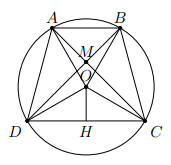
Cho ngũ giác đều ABCDE. Hai đường chéo AC và AD cắt BE lần lượt tại M và N.
a) Tính tỉ số giữa các bán kính của đường tròn nội tiếp và đường tròn ngoại tiếp ngũ giác đều đó.
b) Chứng minh rằng các tam giác AMN và CMB là tam giác cân.
c) Chứng minh rằng AB.BC = BM.AC
 Xem đáp án
Xem đáp án

a) Gọi a, R, r theo thứ tự là độ dài mỗi cạnh, bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp ABCDE.
Câu 12:
Cho đều, nội tiếp đường tròn (O; R). Gọi D, E, F theo thứ tự là điểm chính giữa cung AB, BC, CA. Chứng minh rằng ADBECF là lục giác đều.
 Xem đáp án
Xem đáp án
Vì tam giác ABC đều nên
Mà D, E, F theo thứ tự là điểm chính giữa cung AB, BC, CA nên
Do đó các tam giác AOD, DOB, BOE, EOC, COF, FOA là tam giác đều có cạnh bằng R.
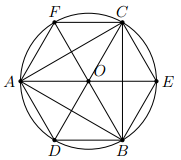
Vậy ADBECF có 6 cạnh bằng nhau và 6 góc bằng nên là lục giác đều.