Bài tập Diện tích hình tròn, hình quạt tròn có đáp án
-
2240 lượt thi
-
16 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tính diện tích hình tròn nội tiếp một hình vuông có cạnh là 4 cm.
 Xem đáp án
Xem đáp án
Hình tròn nội tiếp hình vuông có đường kính d bằng cạnh hình vuông: d = 4 cm.
Hình tròn nội tiếp hình vuông cạnh 4 cm là:
Câu 3:
Diện tích hình tròn sẽ thay đổi như thế nào nếu:
a) Bán kính tăng gấp đôi?
b) Bán kính tăng gấp ba?
c) Bán kính tăng gấp k lần (k > 1)?
 Xem đáp án
Xem đáp án
Diện tích hình tròn có bán kính (kR) là
a) Nếu bán kính tăng gấp đôi thì diện tích hình tròn tăng gấp 4 lần.
b) Nếu bán kính tăng gấp ba thì diện tích hình tròn tăng gấp 9 lần.
c) Nếu bán kính tăng gấp k lần thì diện tích hình tròn tăng gấp lần.
Câu 6:
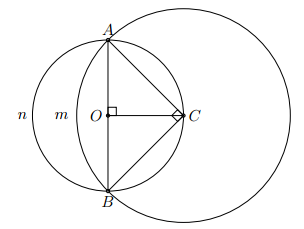
Lấy cạnh BC của một tam giác đều làm đường kính, vẽ một nửa đường tròn về cùng một phía với tam giác ấy đối với đường thẳng BC. Cho biết cạnh BC = a, hãy tính diện tích của hai hình viên phân được tạo thành.
 Xem đáp án
Xem đáp án
Gọi O là trung điểm của BC, ta có OB = OC =
Gọ D, E theo thứ tự là giao điểm của AB và AC với đường tròn đường kính BC. Dễ thấy OAB, OEC là các tam giác đều.
Từ đó, ta có diện tích của hai hình viên phân gạch sọc là:
Câu 7:
Hình vành khăn là phần hình tròn bao gồm giữa hai đường tròn đồng tâm. Tính diện tích hình vành khăn tạo thành bởi đường tròn nội tiếp và đường tròn ngoại tiếp tam giác đều có cạnh 6 cm.
 Xem đáp án
Xem đáp án
Gọi R, r theo thứ tự là bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp tam giác đều, ta có:
Câu 8:
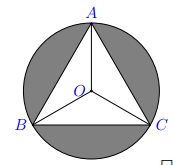
a) Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1 cm. Nêu cách vẽ.
b) Tính diện tích miền gạch sọc.
 Xem đáp án
Xem đáp án
a) Cách vẽ:
- Vẽ cung CD có số đo bằng của đường tròn (A; 1cm)
- Vẽ cung DE có số đo bằng của đường tròn (B; 2cm)
- Vẽ cung EF có số đo bằng của đường tròn (C; 3cm)
b) Diện tích miền gạch sọc là:
Câu 9:
Một đường tròn có độ dài là 72 cm. Tính diện tích hình viên phân tạo thành bởi một cạnh của tam giác đều nội tiếp và cung nhỏ bị trương.
 Xem đáp án
Xem đáp án
Bán kính của đường tròn là
Diện tích hình viên phân giới hạn bởi cung nhỏ AB và cạnh AB là:
Câu 10:
Cho đường tròn (O; 2cm), một điểm M có MO = 2cm. Qua M kẻ hai tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm). Tính diện tích hình giới hạn bởi các đoạn thẳng MA, MB và cung nhỏ AB.
 Xem đáp án
Xem đáp án
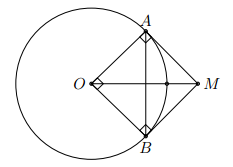
Các tam giác OBM, OAM là các tam giác vuông cân. Do đó, tứ giác OBMA là hình vuông. Gọi S là diện tích của hình giới hạn bởi MA, MB và cung nhỏ AB. Ta có:
Câu 13:
Cho vuông tại A có AB = 10m, . Vẽ nửa đường tròn tâm O đường kính BC và đi qua điểm A. tính tổng diện tích hai hình viên phân ứng với cung AB và cung AC.
 Xem đáp án
Xem đáp án

Tổng diện tích hai hình viên phân bằng diện tích nửa hình tròn trừ đi diện tích tam giác ABC.
Câu 15:
Tính diện tích của phần gạch sọc trên hình.
 Xem đáp án
Xem đáp án
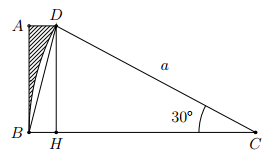
Diện tích phải tìm bằng hiệu của diện tích hình thang vuông ABCD và hình quạt
Kẻ , ta được:
Câu 16:
Một hình vuông và một hình tròn có cùng chu vi. Hỏi hình nào có diện tích lớn hơn?
 Xem đáp án
Xem đáp án
Gọi C là độ dài chu vi của hình vuông và hình tròn.
Gọi a là độ dài cạnh hình vuông, suy ra
Gọi R là bán kính của hình tròn, suy ra
Vậy diện tích hình tròn lớn hơn.