11 câu hỏi trắc nghiệm thuộc Bài tập Liên hệ giữa cung và dây có đáp án

Câu 1:

Cho $∆$ ABC vuông cân tại A và nội tiếp trong đường tròn (O). Chứng minh rằng

a) $\overset{⏜}{AB} = \overset{⏜}{BC}$

b) $\overset{⏜}{AB} < \overset{⏜}{BC}$

Xem đáp án

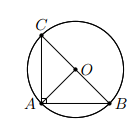
Trong đường tròn (O):

Xét $∆$ ABC vuông cân tại A, ta có ngay:

- AB = AC (hai cạnh bên của tam giác cân) => $\overset{⏜}{AB} = \overset{⏜}{BC}$

- AB < BC (cạnh góc vuông nhỏ hơn cạnh huyền) => $\overset{⏜}{AB} < \overset{⏜}{BC}$

Câu 2:

a) Vẽ đường tròn tâm (O), bán kính R = 2 cm. Nêu cách vẽ cung $\overset{⏜}{AB}$ có số đo bằng $60^{0}$ . Hỏi dây AB dài bao nhiêu xen – ti – mét?

b) Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như hình dưới

Xem đáp án

b)

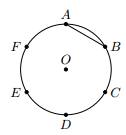
Vậy các điểm A, B, C, D, E, F chia đường tròn thành 6 cung bằng nhau.

Câu 3:

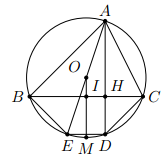
Cho đường tròn (O), dây AB. Gọi M là điểm chính giữa của cung AB. Vẽ dây MC cắt dây AB tại D. Vẽ đường vuông góc với AB tại D, cắt OC ở K. Chứng minh rằng là tam giác cân.

Xem đáp án

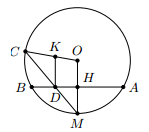
Vì M là điểm chính giữa của cung AB nên

Suy ra <=> $∆ KCD$ là tam giác cân

Câu 4:

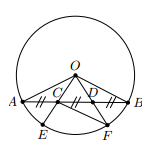
Chứng minh rằng hai cung chắn giữa hai dây song song thì bằng nhau.

Xem đáp án

Xét hai dây song song AB và CD, kẻ bán kính $ON ⊥ AB$ , khi đó vì:

Câu 5:

Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Đường cao AH của tam giác cắt đường tròn ở D. Vẽ đường kính AE.

a) Chứng minh rằng BECD là hình thang cân.

b) Gọi M là điểm chính giữa của cung DE, OM cắt BC tại I. Chứng minh rằng I là trung điểm của BC.

c) Tính bán kính của đường tròn biết BC = 24cm, IM = 8cm.

Xem đáp án

Câu 6:

Cho hai đường tròn bằng nhau (O) và (O’) cắt nhau tại hai điểm A và B. Kẻ các đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O’). Gọi E là giao điểm thứ hai của AC với đường tròn (O’)

a) So sánh các cung nhỏ $\overset{⏜}{BC}, \overset{⏜}{BD}$ .

b) Chứng minh rằng B là điểm chính giữa của cung $\overset{⏜}{EBD}$ (tức là điểm B chia cung $\overset{⏜}{EBD}$ thành hai cung bằng nhau $\overset{⏜}{BE} = \overset{⏜}{BD}$ )

Xem đáp án

Câu 7:

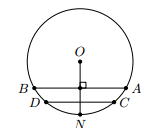
Tứ giác ABCD có $\overset{⏜}{B} = \overset{⏜}{D} = 90^{0}$ . Biết AB < AD, chứng minh rằng BC > CD.

Xem đáp án

Suy ra ABCD nội tiếp đường tròn đường kính AC.

Ta có

Câu 8:

Hai đường tròn (O) và (O’) cùng bán kính cắt nhau tại M và N.

a) Chứng minh rằng hai cung nhỏ $\overset{⏜}{MN}$ của hai đường tròn bằng nhau.

b) Vẽ các đường kính MA của đường tròn (O) và đường kính MB của đường tròn (O’). Chứng minh rằng $\overset{⏜}{NA} = \overset{⏜}{NB}$

c) Vẽ đường kính NOC. Tia BM cắt đường tròn (O) tại D. Chứng minh rằng các cung nhỏ $\overset{⏜}{MN}, \overset{⏜}{AC}, \overset{⏜}{CD}$ bằng nhau.

Xem đáp án

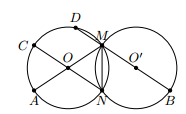
a) Vì MN là dây cung chung của hai đường tròn bằng nhau nên hai cung nhỏ của hai đường tròn bằng nhau.

b) Ta có $\overset{⏜}{AM} = \overset{⏜}{MB}$ , vì hai đường tròn bằng nhau

c) Tứ giác ACMN là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường, nên

Mặt khác, ta có A, N, B thẳng hàng và AN = BN

Suy ra ON là đường trung bình của $∆ ABD$ , do đó

Câu 9:

Cho $∆ ABC$ . Trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp $∆ DBC$ . Từ O lần lượt hạ các đường vuông góc với OH, OK với BC và BD ( $H \in BC, K \in BD$ )

a) Chứng minh rằng OH > OK

b) So sánh hai cung nhỏ $\overset{⏜}{BD}, \overset{⏜}{BC}$

Xem đáp án

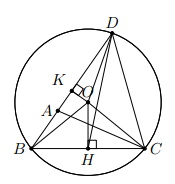
a) Xét $∆ OBD$ và $∆ OBC$ cân tại đỉnh O có các đường cao kẻ từ đỉnh theo thứ tự là OK và OH nên chúng đồng thời là các trung tuyến.

Câu 10:

Trên dây cung $\overset{⏜}{AB}$ của đường tròn (O) lấy hai điểm C và D sao cho AC = CD = DB. Các bán kính qua C và D cắt cung nhỏ AB lần lượt tại E và F. Chứng minh rằng $\overset{⏜}{AE} = \overset{⏜}{BF} < \overset{⏜}{EF}$

Xem đáp án

Câu 11:

a) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy. mệnh đề đảo có đúng không? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.

b) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.

Xem đáp án

a) Giả sử đường kính CD của đường tròn (O) có C là điểm chính giữa của cung AB.

Nghĩa là AC = CB. Suy ra $\hat{O_{1}} = \hat{O_{2}}$

Gọi I là giao điểm của CD và AB, ta có:

OI vừa là tia phân giác vừa là trung tuyến của tam giác OAB

Vậy I là trung điểm của AB

Mệnh đề đảo không đúng, ta cần bổ sung thêm “Đường kính đi qua trung điểm một dây không đi qua tâm của đường tròn thì nó vuông góc với dây đó”.

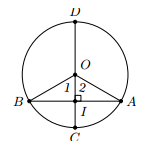
b) Đường kính CD đi qua C là điểm chính giữa cung AB nên AC = CB

Suy ra $\hat{AOC} = \hat{COB}$ => OC là tia phân giác của góc $\hat{AOB}$

Vì tam giác OAB cân tại O nên đường phân giác đồng thời là đường cao

Vậy ta có $OC ⊥ AB \Rightarrow CD ⊥ AB$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập ôn tập chương 3 hình học 9 có đáp án

Bài tập Liên hệ giữa cung và dây có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương