20 câu hỏi trắc nghiệm thuộc Bài tập Ôn tập chương III có đáp án

Câu 1:

Cho đường tròn tâm O, đường kính AB = 2R. Lấy $M \in (O)$ với AM < BM. Trên cạnh MB lấy điểm C sao cho MC = MA. Gọi OD là bán kính vuông góc với AB (M và D ở hai bên đường thẳng AB)

a) Chứng minh $\hat{AMB} = 90^{0}$ . Tính theo R độ dài các cạnh của

b) Chứng tỏ MD là phân giác $\hat{AMB} = 90^{0}$ và $MD ⊥ AC$

c) Chứng minh rằng D là tâm của đường tròn (ABC)

d) Đường tròn (ABC) cắt MD tại I. Chứng minh I là tâm đường tròn nội tiếp $∆ MAB$

Xem đáp án

Câu 2:

Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B, C là hai tiếp điểm). Vẽ cát tuyến ADE của đường tròn (O) (D, E thuộc đường tròn (O); D nằm giữa A và E, tia AD nằm giữa hai tia AB, AO).

a) Chứng minh rằng A, B, O, C cùng thuộc một đường tròn và xác định tâm của đường tròn này.

b) Chứng minh rằng ${AB}^{2} = AD . AE$

c) Gọi H là giao điểm của OA và BC. Chứng minh rằng $∆ ADH ~ ∆ AEO$ và tứ giác DEOH nội tiếp.

d) Đường thẳng AO cắt đường tròn (O) tại M, N (M nằm giữa A và O). Chứng minh rằng $\frac{EH}{AN} = \frac{MH}{AD}$

Xem đáp án

Câu 3:

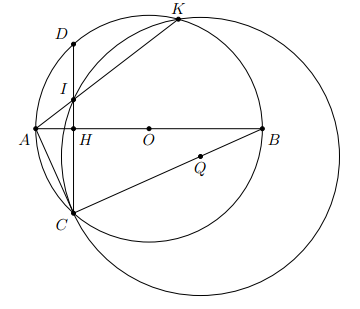
Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E. Hai tiếp tuyến EM và Bx của (O) cắt nhau tại D (M thuộc (O))

a) Chứng minh rằng 4 điểm O, M, D, B cùng thuộc một đường tròn.

b) Chứng minh $∆ EMA ~ ∆ EBM$ , suy ra ${EM}^{2} = {EO}^{2} - R^{2}$

c) Trên đoạn ME lấy điểm C sao cho hai góc $\hat{CAM}, \hat{EDO}$ bằng nhau. Chứng minh rằng OC // MB.

d) Giả sử M là trung điểm đoạn ED. Tính EM theo R.

Xem đáp án

a) Vì EM và BD là tiếp tuyến với đường tròn (O) nên

Vậy tứ giác DMOB nội tiếp, suy ra 4 điểm O, M, D, B cùng thuộc một đường tròn.

Câu 4:

Cho tam giác ABC nội tiếp đường tròn (O; R). Gọi đường tròn (I; r) đường tròn nội tiếp tam giác ABC, H là tiếp điểm của AB với đường tròn (I), D là giao điểm của AI với đường tròn (O), DK là đường kính của đường tròn (O). Gọi d là độ dài của OI. Chứng minh rằng:

a) $∆ AHI ~ ∆ KCD$

b) $DI = DB = DC$

c) $IA . ID = R^{2} - d^{2}$

d) $d^{2} = R^{2} - 2 Rr$

Xem đáp án

Câu 5:

Cho điểm C thuộc nửa đường tròn đường kính AB. Kẻ tiếp tuyến Ax của nửa đường tròn đó (Ax nằm trên cùng một nửa mặt phẳng có bờ là đường thẳng AB chứa nửa đường tròn). Tia phân giác của góc Cax cắt nửa đường tròn tại D. kéo dài AD và BC cắt nhau tại E. kẻ EH vuông góc với Ax tại H.

a) Chứng minh tứ giác AHEC nội tiếp đường tròn.

b) Chứng minh $\hat{ABD} = \hat{BDC}$

c) Chứng minh tam giác ABE cân.

d) Tia BD cắt AC và Ax lần lượt tại F và K. Chứng minh AKEF là hình thoi.

Xem đáp án

Câu 6:

Cho đường tròn tâm O, đường kính AB cố định. H là điểm cố định thuộc đoạn OA (H không trùng O và A). Qua H vẽ đường thẳng vuông góc với AB cắt đường tròn tâm O tại C và D. Gọi K là điểm tùy ý thuộc cung lớn CD (K không trùng các điểm C, D và B). Gọi I là giao điểm của AK và CD.

a) Chứng minh tứ giác HIKB nội tiếp đường tròn.

b) Chứng minh AI.AK = AH.AB

c) Chứng minh khi điểm K thay đổi trên cung lớn CD của đường tròn tâm O thì tâm đường tròn ngoại tiếp tam giác KCI luôn thuộc một đường thẳng cố định.

Xem đáp án

Câu 7:

Cho đường tròn (O) bán kính R và mọt dây cung BC cố định. Gọi A là điểm chính giữa cung nhỏ $\overset{⏜}{BC}$ . Lấy điểm M bất kì trên cung nhỏ $\overset{⏜}{AC}$ , kẻ tia Bx vuông góc với tia MA ở I và cắt tia CM tại D.

a) Chứng minh $\hat{AMD} = \hat{ABC}$ và MA là tia phân giác của góc $\hat{BMD}$

bc Chứng minh A là tâm đường tròn ngoại tiếp tam giác BCD và góc $\hat{BCD}$ có độ lớn không phụ thuộc vào vị trí điểm M.

c Tia DA cắt BC tại E và cắt đường tròn (O) tại điểm thứ hai là F. Chứng minh AB là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF.

Xem đáp án

Câu 8:

Cho tam giác ABC vuông tại A. Đường tròn tâm O đường kính AB cắt các đoạn BC và OC lần lượt tại D và I. Gọi H là hình chiếu vuông góc của A lên OC, AH cắt BC tại M.

a) Chứng minh tứ giác ACDH là nội tiếp và $\hat{CHD} = \hat{ABC}$

b) Chứng minh hai tam giác OHB và OBC đồng dạng với nhau và HM là tia phân giác của góc $\hat{BHD}$

c) Gọi K là trung điểm của BD chứng minh MD.BC = MB.CD và MB.MD = MK.MC.

d) Gọi E là giao điểm của AM và OK, J là giao điểm của IM và (O) (J khác I). Chứng minh hai đường thẳng OC và EJ cắt nhau tại một điểm trên (O).

Xem đáp án

Câu 9:

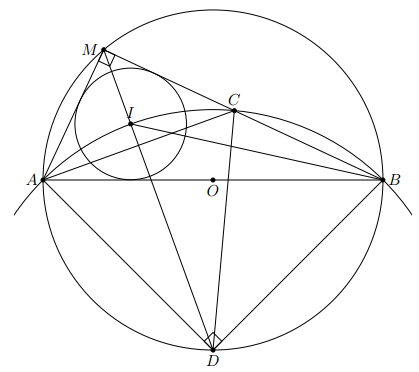
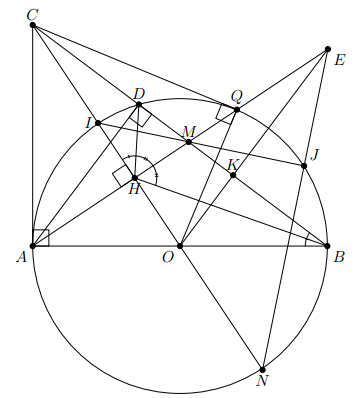
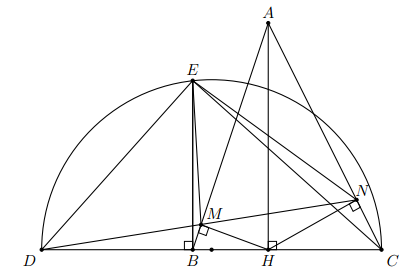
Cho đường tròn (O) ngoại tiếp tam giác nhòn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.

a) Chứng minh bốn điểm C, N, K, I cùng thuộc một đường tròn.

b) Chứng minh ${NB}^{2}$ = NK.NM

c) Chứng minh tứ giác BHIK là hình thoi.

d) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O). Chứng minh ba điểm D, E, K thẳng hàng.

Xem đáp án

Chứng minh tương tự các ý ở trên, ta được KI // BH (5)

Từ (4) và (5) suy ra BHIK là hình bình hành.

Từ (6) và (7) suy ra BH = BK

Mà BHIK là hình bình hành nên BHIK là hình thoi.

Mà hai góc này ở vị trí đồng vị nên PK // CD => PK // DQ (10)

Chứng minh tương tự ta có C, Q, D thẳng hàng và QK // DP (11)

Từ (10) và (11) suy ra DPKQ là hình bình hành.

Mà E là trung điểm của đường chéo PQ nên E cũng là trung điểm của đường chéo DK.

Vậy D, E, K thẳng hàng.

Câu 10:

Cho tứ giác ABCD nội tiếp đường tròn (O) đường kính AC = 2R. Gọi K và M lần lượt là chân đường cao hại từ A và C xuống BD, E là giao điểm của AC và BD, biết K thuộc đoạn BE ( $K \neq B, K \neq E$ ). Đường thẳng qua K song song với BC cắt AC tại P.

a) Chứng minh tứ giác AKPD nội tiếp.

b) Chứng minh $KP ⊥ PM$

c) Biết $\hat{ABD} = 60^{0}$ và AK = x. Tính BD theo R và x.

Xem đáp án

Câu 11:

Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn (C) tâm o bán kính R. Hai đường cao AE và BK của tam giác ABC cắt nhau tại H (với E thuộc BC, K thuộc AC)

a) Chứng minh tứ giác ABEK nội tiếp được trong một đường tròn.

b) Chứng minh CE.CB = CK.CA

c) Chứng minh $\hat{OCA} = \hat{BAE}$

d) Cho B, C cố định và A di động trên ( C) nhưng vẫn thỏa mãn điều kiện tam giác ABC nhọn, khi đó H thuộc một đường tròn (T) cố định. Xác định tâm I và tính bán kính r của đường tròn (T), biết R = 3 cm.

Xem đáp án

$\Rightarrow IH = OA = R = 3 (cm)$ => H thuộc đường tròn (I; 3cm) cố định.

Câu 12:

Cho tam giác nhọn ABC có AB < AC và đường cao AK. Vẽ đường tròn tâm O đường kính BC. Từ A kẻ các tiếp tuyến AM, AN với đường tròn (O) (M, N là các tiếp điểm; M và B nằm trên nửa mặt phẳng có bờ là đường thẳng AO). Gọi H là giao điểm của hai đường thẳng MN và AK. Chứng minh rằng:

a) Tứ giác AMKO nội tiếp đường tròn.

b) KA là tia phân giác của $\hat{MKN}$

c) ${AN}^{2}$ = AK.AH

d) H là trực tâm của tam giác ABC.

Xem đáp án

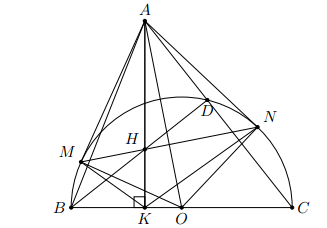
a) AM, AN là tiếp tuyến của đường tròn (O) nên $\hat{AMO} = \hat{ANO} = 90 °$

AK là đường cao của tam giác ABC nên $\hat{AKO} = \hat{AKC} = 90 °$

Ba điểm M, K, N cùng nhìn đoạn AO dưới một góc vuông nên năm điểm M,

K, N, A, O thuộc đường tròn đường kính AO.

Vậy tứ giác AMKO nội tiếp đường tròn.

b) AM, AN là tiếp tuyến của đường tròn (O) nên AM = AN (1)

Theo chứng minh câu trên, năm điểm M, K, N, O, A cùng thuộc một đường tròn nên ta có tứ giác AMKN nội tiếp

Từ (1) và (2) suy ra $\hat{AKM} = \hat{AKN}$ (các góc nội tiếp cùng chắn các cung bằng nhau thì bằng nhau). Vậy KA là tia phân giác của $\hat{MKN}$

Câu 13:

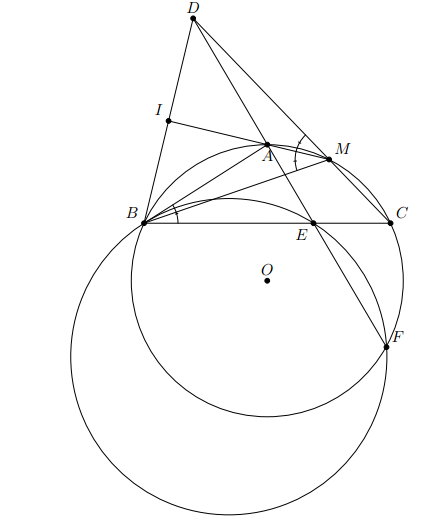
Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB với đường tròn (A, B là hai tiếp điểm). Lấy điểm C trên cung nhỏ AB (C không trùng với A, B). Từ điểm C kẻ CD vuông góc với AB, CE vuông góc với MA, CF vuông góc với MB ( $D \in AB, E \in MA, F \in MB$ ). Gọi I là giao điểm của AC và DE, K là giao điểm của BC và DF. Chứng minh rằng

a) Tứ giác ADCE nội tiếp đường tròn.

b) Hai tam giác CDE và CFD đồng dạng

c) Tia đối của tia CD là tia phân giác của góc $\hat{ECF}$

d) Đường thẳng IK song song với đường thẳng AB.

Xem đáp án

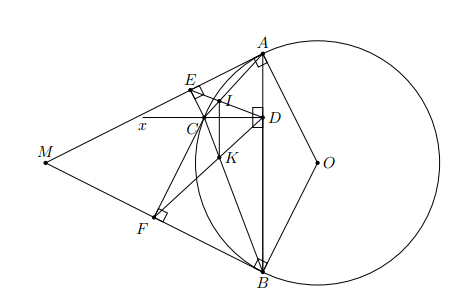
a) Tứ giác ADCE có $\hat{ADC} = \hat{AEC} = 90 °$ nên ADCE là tứ giác nội tiếp.

b) Tứ giác ADCE nội tiếp nên $\hat{EAC} = \hat{EDC}$

Tương tự, tứ giác BDCF nội tiếp, suy ra $\hat{CFD} = \hat{CBD}$

Mặt khác, theo tính chất của góc tạo bởi tiếp tuyến và dây cung thì

Câu 14:

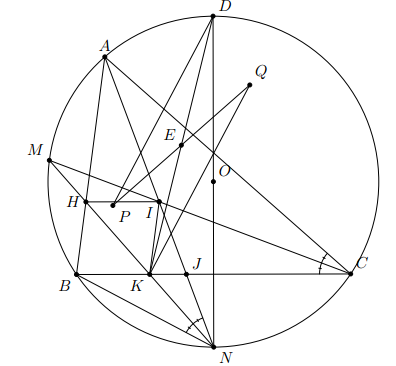
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ $\overset{⏜}{AB}$ và cung nhỏ $\overset{⏜}{BC}$ . Hai dây AN và CM cắt nhau tại I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.

a) Chứng minh các điểm C, N, K, I cùng thuộc một đường tròn.

b) Chứng minh ${NB}^{2} = NK . MN$

c) Chứng minh tứ giác BHIK là hình thoi.

d) Gọi PQ lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O). Chứng minh ba điểm D, E, K thẳng hàng.

Xem đáp án

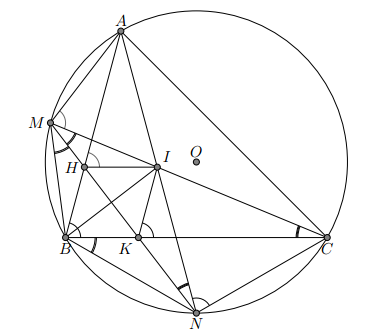
a) Ta có M là điểm chính giữa cung AB

$\Rightarrow AM = BM \Rightarrow \hat{MNA} = \hat{MCB}$ $\Rightarrow \hat{KNI} = \hat{ICK}$

Tứ giác CNKI có C và N là hai đỉnh kề nhau cùng nhìn cạnh KI dưới hai góc bằng nhau nên CNKI nội tiếp (dấu hiệu nhận biết tứ giác nội tiếp).

Do dó bốn điểm C, N, I, K cùng thuộc một đường tròn.

b) Ta có N là điểm chính giữa cung BC

nên BK // HI (2)

Từ (1) và (2) suy ra tứ giác BHIK là hình bình hành.

Mặt khác, AN, CM lần lượt là các tia phân giác của các góc A và C trong tam giác ABC nên I là giao điểm ba đường phân giác, do đó BI là tia phân giác góc B.

Vậy tứ giác BHIK là hình thoi

Do vậy D, Q, C thẳng hàng nên KQ // PK.

Chứng minh tương tự ta có D, P, B thẳng hàng và DQ // PK.

Do đó tứ giác PDQK là hình bình hành nên E là trung điểm của PQ cũng là trung điểm của DK. Vậy D, E, K thẳng hàng.

Câu 15:

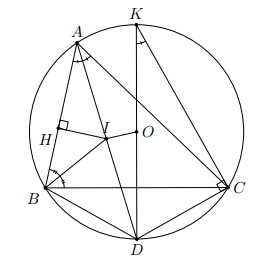
Cho đường tròn tâm O và điểm A nằm ngoài đường tròn. Từ A kẻ hai tiếp tuyến AB và AC (B, C là các tiếp điểm).

a) Chứng minh tứ giác ABOC là tứ giác nội tiếp.

b) Gọi H là trực tâm tam giác ABC. Chứng minh tứ giác BOCH là hình thoi.

c) Gọi I là giao điểm của đoạn OA với đường tròn (O). Chứng minh I là tâm đường tròn nội tiếp tam giác ABC.

d) Cho OB = 3cm, OA = 5cm. Tính diện tích tam giác ABC.

Xem đáp án

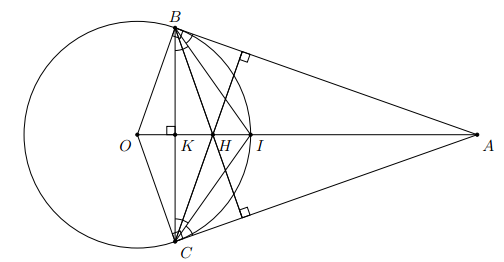
a) Vì AB, AC là các tiếp tuyến của (O) (tại B, C) nên $\hat{ABO} = \hat{ACO} = 90 °$

=> AOBC là tứ giác nội tiếp đường tròn đường kính AO.

Tương tự OC // BH (2)

Từ (1) và (2) ta có BOCH là hình bình hành. Mà OB = OC nên BOCH là hình thoi.

Vì AB, AC là các tiếp tuyến của (O) nên AO là tia phân giác $\hat{BAC}$ . Vì I là giao điểm của đoạn AO với (O) nên I là điểm chính giữa của cung (nhỏ) $\hat{BC}$

do vậy I là tâm đường tròn nội tiếp tam giác ABC.

c) Gọi I là giao điểm của OA và BC => K là trung điểm của BC và $BK ⊥ AO$

Áp dụng định lí Pitago cho tam giác AOB vuông tại B:

$AB = \sqrt{{AO}^{2} - {OB}^{2}} = 4 cm$

Áp dụng hệ thức lượng cho tam giác AOB vuông tại B:

Câu 16:

Cho hình chữ nhật ABCD nội tiếp đường tròn tâm O. Tiếp tuyến của đường tròn tâm O tại điểm C cắt các đường thẳng AB và AD theo thứ tự tại M, N. Dựng AH vuông góc với BD tại điểm H; K là giao điểm của hai đường thẳng MN và BD.

a) Chứng minh tứ giác AHCK là tứ giác nội tiếp.

b) Chứng minh rằng: AD.AN = AB.AM

c) Gọi E là trung điểm của MN. Chứng minh ba điểm A, H, E thẳng hàng.

d) Cho AB = 6 cm, AD = 8 cm. Tính độ dài đoạn MN.

Xem đáp án

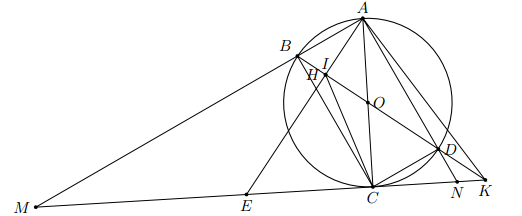
a) Xét tứ giác AHCK ta có $\hat{AHK} = 90 °$

Ck là tiếp tuyến của đường tròn O và AC là đường kính nên $AC ⊥ CK \Rightarrow \hat{ACK} = 90 °$

Vậy H và C cùng nhìn AK dưới một góc vuông nên tứ giác AHCK nội tiếp một đường tròn.

b) Ta có ABCD là hình chữ nhật $\Rightarrow \hat{ADB} = \hat{ACB}$

c) Giả sử AE vắt BD tại I, ta chứng minh H trùng với I. Thật vậy.

Ta có $∆ AMN$ vuông tại A có E là trung điểm của cạnh MN => $∆ AEN$ cân tại E

$\Rightarrow \hat{EAN} = \hat{ENA}$

Theo chứng minh trên ta có $\hat{ADB} = \hat{AMN}$

Câu 17:

Cho tam giác ABC (AB < AC) nội tiếp trong đường tròn tâm (O), M là một điểm nằm trên cung BC không chứa điểm A. Gọi D, E, F làn lượt là hình chiếu vuông góc của M trên các đường thẳng BC, CA, AB. Chứng minh rằng:

a) Bốn điểmM, D, B, F thuộc một đường tròn và bốn điểm M, D, E, C thuộc một đường tròn.

b) Ba điểm D, E, F thẳng hàng.

c) $\frac{BC}{MD} = \frac{CA}{ME} + \frac{AB}{MF}$

Xem đáp án

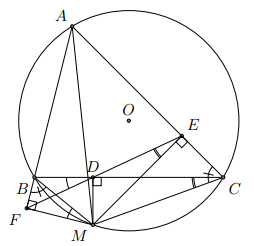
a) Ta có D và F lần lượt là hình chiếu của M trên BC và AB.

Câu 18:

Cho tam giác ABC có ba góc nhọn (AB < AC), dựng AH vuông góc với BC tại điểm H. Gọi M, N theo thứ tự là hình chiếu vông góc của điểm H trên AB và AC. Đường thẳng MN cắt đường thẳng BC tại điểm D. Trên nửa mặt phẳng bờ CD chứa điểm A, vẽ nửa dường tròn đường kính CD. Qua B kẻ đường thẳng vuông góc với CD cắt nửa đường tròn trên tại E.

a) Chứng minh rằng tứ giác AMHN là tứ giác nội tiếp.

b) Chứng minh $\hat{EBM} = \hat{DNH}$

c) Chứng minh rằng $DM . DN = DB . DC$

d) Gọi O là tâm đường tròn ngoại tiếp tam giác MNE. Chứng minh rằng $OE ⊥ DE$

Xem đáp án

Câu 19:

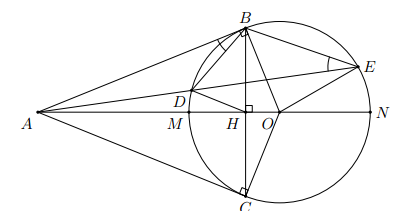
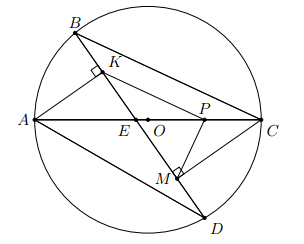
Tam giác AMB cân tại M nội tiếp trong đường tròn (O; R). Kẻ MH vuông góc AB ( $H \in AB$ ) ,MH cắt đường tròn tại N. Biết MA = 10 cm, AB = 12 cm.

a) Tính MH và bán kính R của đường tròn.

b) Trên tia đối tia BA lấy điểm C. Tia MC cắt đường tròn tại D, ND cắt AB tại E. Chứng minh tứ giác MDEH nội tiếp và chứng minh các hệ thức sau: ${NB}^{2} = NE . ND$ và $AC . BE = BC . AE$

c) Chứng minh NB tiếp xúc với đường tròn ngoại tiếp tam giác BDE.

Xem đáp án

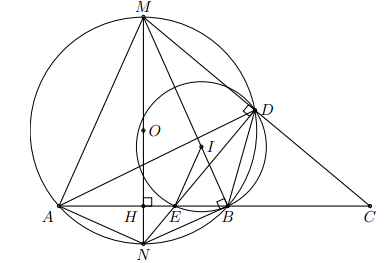
a) Theo tính chất đường kính và dây cung suy ra H là trung điểm AB và AH = 6cm.

Vậy NB tiếp xúc với đường tròn ngoại tiếp tam giác BDE.

Câu 20:

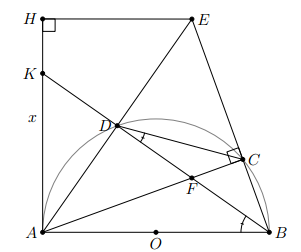
Cho ba điểm cố định A, B, C thẳng hàng (B nằm giữa A và C). Gọi (O) là một đường tròn thay đổi luôn đi qua B và C (tâm O không thuộc đường thẳng BC). Từ A kẻ các tiếp tuyến AD, AE đến đường tròn (O) (D, E là các tiếp điểm và D, O nằm cùng trên nửa mặt phẳng có bờ là đường thẳng BC). Gọi K, H lần lượt là trung điểm của BC và DE.

a) Chứng minh ${AE}^{2} = AB . AC$

b) Trên DE lấy điểm M sao cho BM song song với AD. Chứng minh tứ giác BMKE nội tiếp đường tròn và MK song song với DC.

c) Chứng minh rằng khi đường tròn (O) thay đổi thì tâm đường tròn ngoại tiếp tam giác OHK thuộc một đường thẳng cố định.

Xem đáp án

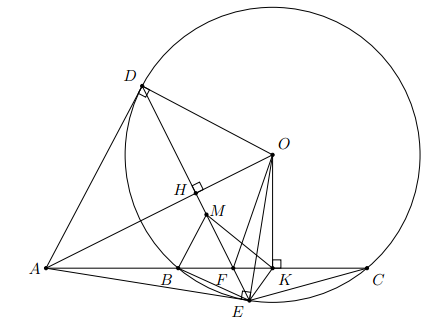
b) Dễ thấy, năm điểm O, A, D, E, K nằm trên đường tròn đường kính OA.

Vậy tứ giác BMKE là tứ giác nội tiếp.

c) Gọi F là giao điểm của DE và AC. Khi đó tứ giác OHFK nội tiếp đường tròn đường kính OF

Suy ra,

$AF . AK = AH . AO =$ ${AE}^{2} = AB . AC$

Hay $AF = \frac{AB . AC}{AK}$ , do đó F là điểm cố định. Vậy tâm đường tròn ngoại tiếp tam giác OHK chạy trên đường trung trực của đoạn thẳng FK.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập ôn tập chương 3 hình học 9 có đáp án

Bài tập Ôn tập chương III có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương