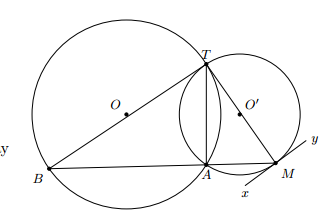Bài tập Góc tạo bởi tiếp tuyến và dây cung có đáp án
-
2245 lượt thi
-
17 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
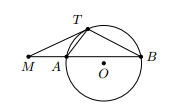
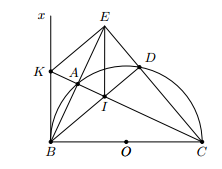
Cho đường tròn (O) và một điểm M nằm bên ngoài đường tròn. Tia Mx quay quanh M và cắt đường tròn tại hai điểm A và B. Gọi I là một điểm thuộc tia Mx sao cho = MA.MB. Tìm quỹ tích điểm I.
 Xem đáp án
Xem đáp án
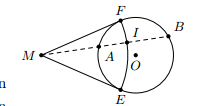
Phần thuận: Kẻ hai tiếp tuyến ME, MF tới đường tròn (O).
Ta có nên
Suy ra I thuộc đường tròn (M; ME)
Hạn chế quỹ tích: vì A chỉ chạy trên cung của đường tròn (O) nên I chỉ chạy trên cung của đường tròn (M,ME) nằm trong đường tròn (O)
Phần đảo: lấy điểm I thuộc của đường tròn (M. ME) nằm trong đường tròn (O).
Nối MI cắt đường tròn (O) tại A và B. Ta cần chứng minh . Thật vậy,
Kết luận: vậy quỹ tích điểm I là cung của đường tròn (M, ME) nằm trong đường tròn (O).
Câu 12:
Cho ngoại tiếp đường tròn (O). Gọi D, E, F là các tiếp điểm của đường tròn trên các cạnh AB, BC, CA. Gọi M, N, P lần lượt là giao điểm của đường tròn (O) với các tia OA, OB, OC. Chứng minh rằng các điểm M, N, P lần lượt là tâm đường tròn nội tiếp các tam giác , ,
 Xem đáp án
Xem đáp án
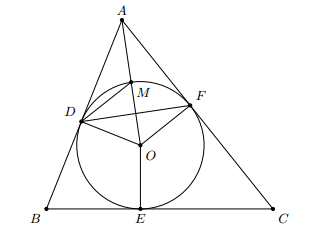
Để chứng minh M là tâm đường tròn nội tiếp các tam giác ADF, ta chứng minh M là giao điểm của hai tia phân giác trong của tam giác ADF.
AD là tiếp tuyến của đường tròn (O) nên AM là tia phân giác của (1)
Lại có, nên DM là tia phân giác của (2)
Từ (1) và (2) suy ra M là tâm đường tròn nội tiếp các tam giác ADF
Chứng minh tương tự với các điểm N và P.
Câu 13:
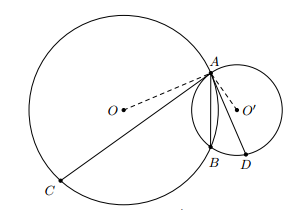
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Một đường thẳng tiếp xúc với đường tròn (O’) tại D. Vẽ đường tròn (I) qua ba điểm A, C, D cắt đường thẳng AB tại điểm thứ hai là E. Chứng minh rằng:
a)
b) Tứ giác BCED là hình bình hành.
 Xem đáp án
Xem đáp án
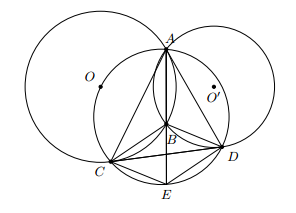
a) Sử dụng tính chất góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung, ta có:
Vậy tứ giác BCDE là hình bình hành.
Câu 14:
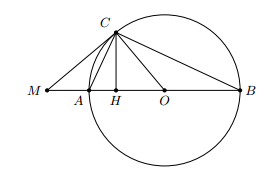
Cho nửa đường tròn (O) đường kính BC. Điểm A thuộc nửa đường tròn (AB < AC). Tiếp tuyến tại A cắt đường thẳng BC ở I. Kẻ . Chứng minh rằng
a) AB là tia phân giác của
b) = IB.IC
 Xem đáp án
Xem đáp án

Suy ra KA = IA và BK = BI.
Xét tứ giác BKEI có hai đường chéo KI và BE cắt nhau tại trung điểm mỗi đường và BK = BI nên tứ giác BKEI là hình thoi.
Câu 16:
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O’) cắt đường tròn (O) tại điểm thứ P. Tia PB cắt đường tròn (O’) tại Q, Chứng minh AQ song song với tiếp tuyến tại P của đường tròn (O).
 Xem đáp án
Xem đáp án
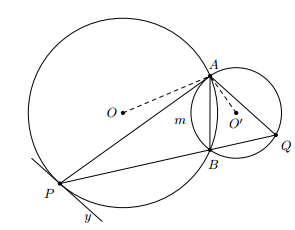
Xét đường tròn (O) ta có:
Câu 17:
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm I có đường kính BH, nó cắt AB ở M. Vẽ đường tròn tâm K có đường kính CH, nó cắt AC ở N.
a) Tứ giác AMHN là hình gì?
b) Chứng minh rằng MN là tiếp tuyến chung của hai đường tròn (I) và (K).
c) Vẽ tiếp tuyến Ax của đường tròn ngoại tiếp . Chứng minh rằng Ax song song với MN.
 Xem đáp án
Xem đáp án
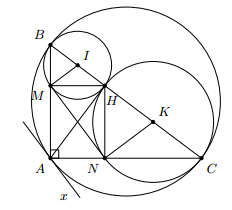
a) Tứ giác AMHN là hình chữ nhật vì có ba góc vuông.