Bài tập Tứ giác nội tiếp có đáp án
-
2160 lượt thi
-
20 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
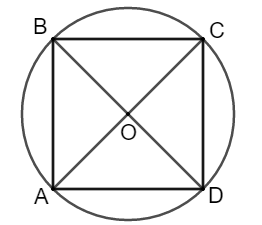
Chứng minh rằng hình chữ nhật ABCD nội tiếp được.
Xem đáp án
Gọi O là giao điểm hai đường chéo AC và BD, ta có ngay
OA = OB = OC = OD => ABCD nội tiếp trong (O; OA)
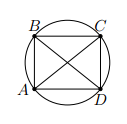
Câu 2:
Cho tam giác ABC đều. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và
a) Chứng minh ABDC là tứ giác nội tiếp.
b) Xác định tâm của đường tròn đi qua bốn điểm A, B, C, D.
Xem đáp án
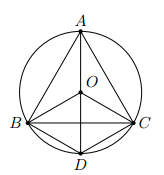
Vậy tứ giác ABDC nội tiếp.
b) Do đường tròn ngoại tiếp ABC cũng đồng thời là đường tròn ngoại tiếp tứ giác ABCD nên để xác định tâm đường tròn đi qua A, B, C, D chỉ cần tìm giao điểm O của AD với đường cao BB’ của tam giác ABC.
Đường tròn (O; OA) đi qua A, B, C, D.
Câu 3:
Cho hình thoi ABCD tâm O, cạnh bằng a. Gọi M, N, P, Q theo thứ tự là trung điểm của AB, BC, CD, DA
a) Chứng minh rằng AMNC là một tứ giác nội tiếp.
b) Chứng minh rằng MNPQ là một tứ giác nội tiếp.
Xem đáp án
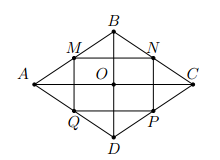
Vậy tứ giác AMNC nội tiếp được một đường tròn.
b) Vì OM, ON, OP, OQ theo thứ tự là đường trung tuyến của các tam giác vuông nên
<=> MNPQ nội tiếp đường tròn (O;)
Câu 4:
Tứ giác ABCD có . Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm.
Xem đáp án
Tứ giác ABCD có tổng hai góc đối nên nó là tứ giác nội tiếp đường tròn tâm O.
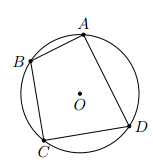
Đường tròn (O) cũng là đường tròn ngoại tiếp nên O là giao điểm các đường trung trực của AB và AC.
Tương tự, (O) là đường tròn ngoại tiếp nên O nằm trên đường trung trực của BD.
Vậy các trung trực của AB, BD, AC cùng đi qua điểm O.
Câu 8:
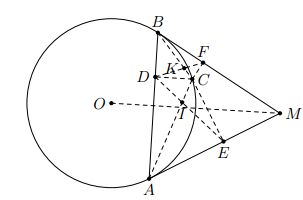
Cho , các đường phân giác của các góc trong gặp nhau tại S, các đường phân giác của các góc ngoài và gặp nhau tại E. Chứng minh rằng:
a) BSCE là tứ giác nội tiếp.
b) Ba điểm A, S, E thẳng hàng.
c) Trung điểm M của SE thuộc đường tròn ngoại tiếp
Xem đáp án
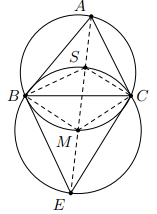
a) Ta có:
- Vì BS, BE là các tia phân giác của hai góc kề bù nên
- Vì CS, CE là các tia phân giác của hai góc kề bù nên
Do đó, tứ giác BSCE nội tiếp (cụ thể nội tiếp đường tròn đường kính SE)
b) Vì AS và AE đều là tia phâ giác của góc nên A, S, E thẳng hàng.
c) Vì M là tâm đường tròn ngoại tiếp tứ giác BSCE nên
Do đó tứ giác ABMC nội tiếp.
Vậy điểm M thuộc đường tròn ngoại tiếp tam giác ABC.
Câu 10:
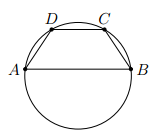
Chứng minh rằng tứ giác ABCD nội tiếp được, biết
a) ABCD là hình thang cân
b) ABCD là hình chữ nhật
Xem đáp án
a) Vì ABCD là hình thang cân nên ta có
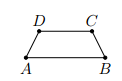
(tổng hai góc trong cùng phía)
Vậy hình thang cân ABCD nội tiếp được.
b) Gọi O là giao điểm hai đường chéo AC và BD.
Ta có OA = OB = OC = OD <=> ABCD nội tiếp trong (O; OA)
Câu 11:
Cho nửa đường tròn (O) đường kính AB và tia tiếp tuyến Bx của nửa đường tròn. Trên tia Bx lấy hai điểm C và D (C nằm giữa B và D). Các tia AC và AD lần lượt cắt đường tròn tại E và F. Hai dây AE và BF cắt nhau tại M. Hai tia AF và BE cắt nhau tại N. Chứng minh rằng
a) MN // Bx.
b) Tứ giác CDFE nội tiếp được.
Xem đáp án
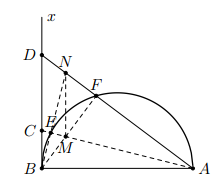
a) Trong tam giác ABN ta có:
Từ (1) và (2) suy ra M là trực tâm tam giác ABN
Suy ra MN // Bx
b) Nhận xét rằng
Câu 12:
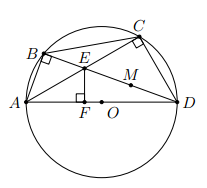
Cho tam giác ABC, các đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC.
a) Chứng minh tứ giác ABDC nội tiếp được trong một đường tròn. Xác định tâm O của đường tròn đó.
b) Đường thẳng DH cắt đường tròn (O) tại điểm thứ hai là I. Chứng minh rằng 5 điểm A, I, F, H, E cùng nằm trên một đường tròn.
Xem đáp án
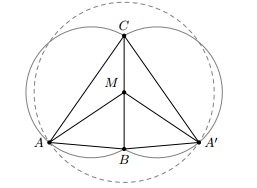
a) Nhận xét rằng, tứ giác CDBH có hai đường chéo CB và DH cắt nhau tại trung điểm mỗi đường nên nó là hình bình hành, suy ra
b) Nhận xét
Vậy các điểm E, F, I cùng nhìn AH dưới một góc vuông, do đó 5 điểm A, I, F, H, E cùng nằm trên một đường tròn đường kính AH.
Câu 13:
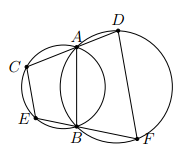
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Tia OA cắt đường tròn (O’) tại C, tia O’A cắt đường tròn (O) tại D. Chứng minh rằng
a) Tứ giác OO’CD nội tiếp
b) Tứ giác OBO’C nội tiếp
c) Năm điểm O, O’, B, C, D cùng nằm trên một đường tròn.
Xem đáp án
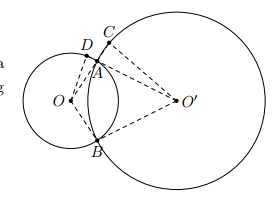
Vậy các điểm C,D nằm cùng phía đối với OO’ và thỏa mãn nên bốn điểm O, O’, C, D thuộc cùng một đường tròn, tức là tứ giác OO’CD nội tiếp.
b) Xét hai tam giác và ta có
OO’ chung
OA = O’B vì cùng bằng bán kính đường tròn (O)
O’A = O’B vì cùng bằng bán kính đường tròn (O’)
c) Nhận thấy rằng:
- Từ kết quả câu a, suy ra D thuộc đường tròn ngoại tiếp tam giác COO’
- Từ kết quả câu b, ta suy ra B thuộc đường tròn ngoại tiếp tam giác COO’
Vậy năm điểm O, O’, B, C, D cùng nằm trên một đường tròn ngoại tiếp tam giác COO’.
Câu 15:
Chứng minh rằng trong một đường tròn hai dây không đi qua tâm không thể cắt nhau tại trung điểm mỗi dây.
Xem đáp án
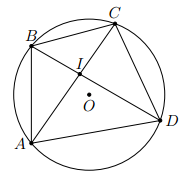
Ta đi chứng minh bằng phản chứng.
Giả sử trái lại có hai dây cung AC và BD cắt nhau tại trung điểm I của mỗi đường và không đi qua tâm O.
Khi đó tứ giác ABCD là hình bình hành.
Do đó, ABCD là hình chữ nhật =>
Vậy BD là đường kính.
, mâu thuẫn.
Câu 17:
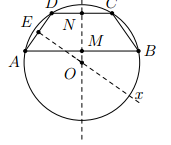
Hai đường tròn (O) và (O’) cắt nhau tại A và B. Một đường thẳng qua A cắt đường tròn (O) và (O’) tại C và D. Vẽ dây CE của đường tròn (O) và dây DF của đường tròn (O’) song song với nhau. Chứng minh rằng ba điểm B, E, F thẳng hàng.
Xem đáp án
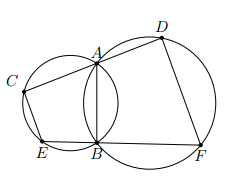
Vẽ dây chung AB, ta lần lượt thấy
Câu 18:
Cho hình vuông ABCD. Trên cạnh AB lấy một điểm M. Đường thẳng qua C vuông góc với CM cắt các tia AB, AD lần lượt tại E và F. Tia CM cắt đường thẳng AD tại N. Chứng minh rằng
a) Tứ giác AMCF nội tiếp được.
b) Tứ giác ANEC nội tiếp được.
c) CM + CN = EF
Xem đáp án
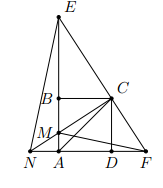
a) Ta lần lượt thấy
Do đó, tứ giác AMCF nội tiếp đường tròn đường kính MF.
b) Ta lần lượt thấy
Do đó, tứ giác ANEC nội tiếp đường tròn đường kính NE.
c) Ta lần lượt xét
