13 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 2

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 2

6690 lượt thi
13 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giải phương trình: $x^{2} - 3 x + 2 = 0$

Xem đáp án

$x^{2} - 3 x + 2 = 0 \Leftrightarrow x^{2} - 2 x - x + 2 = 0$

$\begin{array}{l} \Leftrightarrow x (x - 2) - (x - 2) = 0 \Leftrightarrow (x - 1) (x - 2) = 0 \\ \Leftrightarrow [\begin{array}{l} x = 1 \\ x = 2 \end{array} . \\ V a y .... S = \{1; 2\} \end{array}$

Câu 2:

Giải hệ phương trình: $\{\begin{cases} x + 3 y = 3 \\ 4 x - 3 y = - 18 \end{cases}$

Xem đáp án

$\{\begin{cases} x + 3 y = 3 \\ 4 x - 3 y = - 18 \end{cases} \Leftrightarrow \{\begin{cases} 5 x = - 15 \\ y = \frac{3 - x}{3} \end{cases} \Leftrightarrow \{\begin{cases} x = - 3 \\ y = 2 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất $(x; y) = (- 3; 2)$

Câu 3:

Rút gọn biểu thức $A = \frac{2}{3 + \sqrt{7}} + \frac{\sqrt{28}}{2} - 2$

Xem đáp án

$A = \frac{2}{3 + \sqrt{7}} + \frac{\sqrt{28}}{2} - 2 = \frac{2 (3 - \sqrt{7})}{3^{2} - 7} + \frac{\sqrt{4.7}}{2} - 2$

$= \frac{2 (3 - \sqrt{7})}{2} + \frac{2 \sqrt{7}}{2} - 2 = 3 - \sqrt{7} + \sqrt{7} - 2 = 1$

Vậy A = 1

Câu 4:

Giải phương trình: ${(x^{2} - 2 x)}^{2} + {(x - 1)}^{2} - 13 = 0$

Xem đáp án

$\begin{array}{l} {(x^{2} - 2 x)}^{2} + {(x - 1)}^{2} - 13 = 0 \\ \Leftrightarrow {(x^{2} - 2 x + 1 - 1)}^{2} + {(x - 1)}^{2} - 13 = 0 \\ \Leftrightarrow {[{(x - 1)}^{2} - 1]}^{2} + {(x - 1)}^{2} - 13 = 0 \\ \Leftrightarrow {(x - 1)}^{4} - 2 {(x - 1)}^{2} + 1 + {(x - 1)}^{2} - 13 = 0 \\ \Leftrightarrow {(x - 1)}^{4} - {(x - 1)}^{2} - 12 = 0 \end{array}$

Đặt ${(x - 1)}^{2} = t (t \geq 0) .$ Khi đó ta có phương trình:

$\begin{array}{l} t^{2} - t - 12 = 0 \Leftrightarrow t^{2} - 4 t + 3 t - 12 = 0 \\ \Leftrightarrow t (t - 4) + 3 (t - 4) = 0 \\ \Leftrightarrow (t + 3) (t - 4) = 0 \Leftrightarrow [\begin{array}{l} t = - 3 (k t m) \\ t = 4 (t m) \end{array} \end{array}$

Với $t = 4 \Leftrightarrow {(x - 1)}^{2} = 4 \Leftrightarrow [\begin{array}{l} x - 1 = 2 \\ x - 1 = - 2 \end{array} \Leftrightarrow [\begin{array}{l} x = 3 \\ x = - 1 \end{array}$

Vậy tập nghiệm của phương trình là

S = \{- 1; 3\}

Câu 5:

Cho parabo $(P) : y = - 2 x^{2}$ và đường thẳng $(d) : y = x - m$ (với m là tham số)

Vẽ parabol (P)

Xem đáp án

Học sinh tự vẽ

Câu 6:

b,Tìm tất cả các giá trị của tham số m để đường thẳng (d) cắt P tại hai điểm phân biệt có hoành độ $x_{1}, x_{2}$ thỏa mãn điều kiện $x_{1} + x_{2} = x_{1} x_{2}$

Xem đáp án

b, Phương trình hoành độ giao điểm của (d) và (P)là:

$- 2 x^{2} = x - m \Leftrightarrow 2 x^{2} + x - m = 0 (*)$

Đường thẳng (d) cắt (P) tại hai điểm phân biệt $\Leftrightarrow (*)$ có hai nghiệm phân biệt

$\Leftrightarrow Δ > 0 \Leftrightarrow 1 + 4.2 m > 0 \Leftrightarrow 8 m > - 1 \Leftrightarrow m > \frac{- 1}{8}$

Với $m > - \frac{1}{8}$ thì đường thẳng (d) cắt (P) tại hai điểm phân biệt có hoành độ $x_{1}, x_{2}$

Áp dụng hệ thức Viet ta có: $\{\begin{cases} x_{1} + x_{2} = - \frac{1}{2} \\ x_{1} x_{2} = - \frac{m}{2} \end{cases}$

Theo đề bài ta có: $x_{1} + x_{2} = x_{1} x_{2} \Leftrightarrow - \frac{1}{2} = - \frac{m}{2} \Leftrightarrow m = 1 (t m)$

Vậy m=1 thỏa mãn bài toán.

Câu 7:

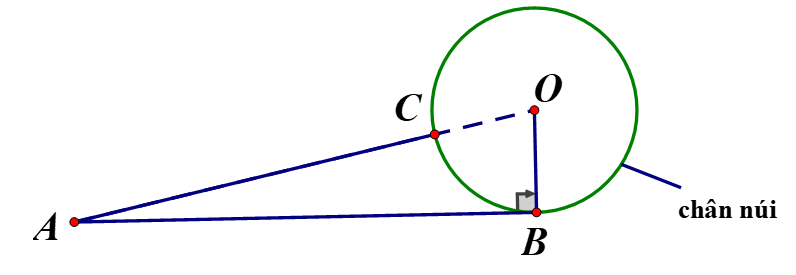
Có một vụ tai nạn ở vị trí B tại chân của một ngọn núi (chân núi có dạng đường tròn tâm O, bán kính 3km Và một trạm cứu hộ ở vị trí A (tham khảo hình vẽ). Do chưa biết đi đường nào dể đến vi trí tai nạn nhanh hơn nên đội cứu hộ quyết định diều hai xe cứu thương cùng xuất phát ở trạm cứu hộ đến vị trí tai nạn theo hai cách sau:

Xe thứ nhất: đi theo đường thẳng từ A đến B, do đường xấu nên vận tốc trung bình của xe là 40km

Xe thứ hai: đi theo đường thẳng từ A đến C với vận tốc trung bình $60 k m / h$ , rồi đi từ C đến B theo đường cung nhỏ CB ở chân núi với vận tốc trung bình $30 k m / h$ (ba điểm A, O, C thẳng hàng và C ở chân núi). Biết đoạn đường AC dài 27km và $\hat{A O B} = 90^{0}$

a, Tính độ dài quãng đường xe thứ nhất đi từ A đến B

Xem đáp án

a) Ta có: $A O = C A + O C = 27 + 3 = 30 k m$

Áp dụng định lý Pytago cho $Δ A B O$ vuông tại B ta có:

$\begin{array}{l} A B^{2} = A O^{2} - O B^{2} = 30^{2} - 3^{2} = 891 \\ \Rightarrow A B = \sqrt{891} = 9 \sqrt{11} \approx 29,85 k m \end{array}$

Vậy quãng đường xe thứ nhất đi là $A B \approx 29,85 k m$

Câu 8:

b, Nếu hai xe cứu thương xuất phát cùng lúc tại A thì xe nào đến vị trí tai nạn trước

Nếu hai xe cứu thương xuất phát cùng lúc tại A thì xe nào đến vị trí tai nạn trước (ảnh 1)

Xem đáp án

b, Thời gian xe thứ nhất đi đến vị trí tai nạn là: $\frac{9 \sqrt{11}}{40} \approx 0,746$ (giờ)

+)ta có: $\cos \hat{A O B} = \cos \hat{C O B} = \frac{3}{30} = \frac{1}{10} \Rightarrow \hat{C O B} \approx {84,26}^{0}$

$\Rightarrow s d \overset{⏜}{B C} = \hat{C O B} = {84,26}^{0}$ (số đo góc ở tâm bằng số đo cung bị chắn)

Suy ra độ dài cung $B C : l_{B C} = \frac{π .3.84,26}{180} \approx 4,41 k m$

$\Rightarrow$ Thời gian xe thứ hai đến vị trí tai nạn là: $27 : 60 + 4,41 : 30 = 0,597$ (giờ)

Ta thấy thời gian xe thứ hai đi đến vị trí tai nạn ít hơn thời gian xe thứ nhất đi đến vị trí tai nạn nên xe thứ hai đến trước xe thứ nhất.

Câu 9:

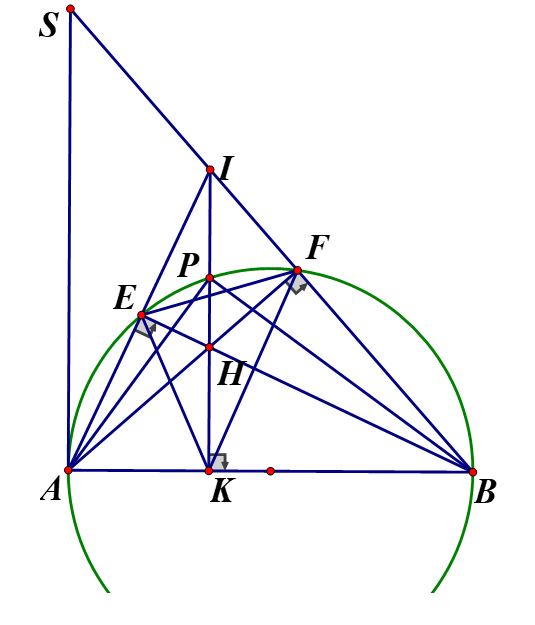
Cho nửa đường tròn tâm O đường kính AB và điểm E tùy ý trên nửa đường tròn đó (E khác A,B). Lấy điểm H thuộc đoạn EB (H khác E, B ). Tia AH cắt nửa đường tròn tại điểm thứ hai là F Kéo dài tia AE và BF cắt nhau tại I. Đường cao IH cắt nửa đường tròn tại P và cắt AB tại K

a) Chứng minh tứ giác IEHFnội tiếp được đường tròn

Xem đáp án

Cho nửa đường tròn tâm O đường kính AB và điểm E tùy ý trên nửa đường tròn đó (E khác A,B). (ảnh 1)

a) Ta có

\hat{A E B} = \hat{A F B} = 90^{0}

(góc nội tiếp chắn nửa đường tròn)

$\Rightarrow A E ⊥ E B, A F ⊥ E B$ hay $B E ⊥ A I, A F ⊥ B I \Rightarrow \hat{I E H} = \hat{I F H} = 90^{0}$

Xét tứ giác IEHF có $\hat{I E H} + \hat{I F H} = 90^{0} + 90^{0} = 180^{0} \Rightarrow$ Tứ giác IEHF là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng $180^{0})$

Câu 10:

b, Chứng minh $\hat{A I H} = \hat{A B E}$

Xem đáp án

b) Ta có $I E H F$ là tứ giác nội tiêp(cmt) $\Rightarrow \hat{E I H} = \hat{E F H}$ (hai góc nội tiếp cùng chắn cung EH) hay $\hat{A I H} = \hat{E F A}$ mà $\hat{E B A} = \hat{E F A}$ (hai góc nội tiếp cùng chắn cung AF của (O))

\Rightarrow \hat{A I H} = \hat{A B E} (= \hat{E F H}) (d f c m)

Câu 11:

c, Chứng minh: $\cos \hat{A B P} = \frac{P K + B K}{P A + P B}$

Xem đáp án

c, Nối $P A, P B$ ta có: $\hat{A P B} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn)

Xét tam giác BPKvà tam giác BAP có:

$\hat{A B P}$ chung; $\hat{B K P} = \hat{B P A} = 90^{0}$

$\Rightarrow Δ B P K ~ Δ B A P (g g) \Rightarrow \frac{P K}{P A} = \frac{B K}{P B}$ (hai cặp cạnh tương ứng tỉ lệ)

Áp dụng tính chất dãy tỉ số bằng nhau ta có: $\frac{P K}{P A} = \frac{B K}{P B} = \frac{P K + B K}{P A + P B} (1)$

Xét tam giác BKF vuông ta có: $\cos \hat{A B P} = \cos \hat{K P B} = \frac{B K}{P K} (2)$

Từ (1) và (2) ta có: $\cos \hat{A B P} = \frac{P K + B K}{P A + P B}$

Câu 12:

d, Gọi S là giao điểm của tia BF và tiếp tuyến tại A của nửa đường tròn Khi tứ giác $A H I S$ nội tiếp được đường tròn. Chứng minh $E F ⊥ E K$

Xem đáp án

d, Xét tứ giác AEHK có $\hat{A E H} + \hat{A K H} = 90^{0} + 90^{0} = 180^{0} \Rightarrow$ Tứ giác AEHK là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng $180^{0})$

$\Rightarrow \hat{H E K} = \hat{H A K} = \hat{F A B}$ (hai góc nội tiếp cùng chắn cung HK)

Lại có: $\hat{F A B} = \hat{F E B}$ (hai góc nội tiếp cùng chắn cung FE của (O))

$\Rightarrow \hat{H E K} = \hat{F E B} \Rightarrow E B$ là phân giác của $\hat{F E K} \Rightarrow \hat{F E K} = 2. \hat{F E B} = 2. \hat{F A B} (3)$

Ta có: $\{\begin{cases} I H ⊥ A B (g t) \\ S A ⊥ A B (g t) \end{cases} \Rightarrow I H / / S A \Rightarrow$ Tứ giác $A H I S$ là hình thang (tứ giác có 2 cạnh đối song song)

Khi AHIS là tứ giác nội tiếp thì $\hat{S A H} + \hat{S I H} = 180^{0}$ (tổng hai góc đối của tứ giác nội tiếp)

Mà $\hat{S A H} + \hat{A H I} = 180^{0}$ (hai góc trong cùng phía bù nhau)

$\Rightarrow \hat{S I H} = \hat{A H I} \Rightarrow$ Tứ giác AHIS là hình thang cân

Do đó $\hat{I S A} = \hat{S A H}$ (tính chất hình thang cân) hay $\hat{B S A} = \hat{S A F}$

Mà $\hat{S A F} = \hat{S B A}$ (góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn $\overset{⏜}{A F})$

$\Rightarrow \hat{B S A} = \hat{S B A} \Rightarrow Δ S A B$ vuông cân tại A $\Rightarrow \hat{S B A} = 45^{0} (4)$

Từ (3) và (4) ta có: $\hat{F E K} = 2 \hat{F A B} = {2.45}^{0} = 90^{0}$

Vậy khi tứ giác AHIS nội tiếp được đường tròn, ta có được $E F ⊥ E K (d f c m)$

Câu 13:

Cho các số thực dương x,y thỏa mãn $x + y \leq 3.$ Tìm giá trị nhỏ nhất của biểu thức:

$P = \frac{1}{5 x y} + \frac{5}{x + 2 y + 5} .$

Xem đáp án

Ta có: $\frac{1}{5 x y} + \frac{x}{10} + \frac{y}{20} \geq 3 \sqrt[3]{\frac{x y}{1000 x y}} = \frac{3}{10}$

$\frac{5}{x + 2 y + 5} + \frac{x + 2 y + 5}{20} \geq 2 \sqrt{\frac{5}{20}} = 1$

$\begin{array}{l} \Rightarrow P + \frac{3. (x + y)}{20} + \frac{1}{4} \geq \frac{3}{10} + 1 \\ \Leftrightarrow P + \frac{9}{20} + \frac{1}{4} \geq \frac{13}{10} \\ \Leftrightarrow P \geq \frac{13}{10} - \frac{1}{4} - \frac{9}{20} \\ \Leftrightarrow P \geq \frac{3}{5} \end{array}$

Dấu $" = "$ xảy ra $\Leftrightarrow \{\begin{cases} x = 1 \\ y = 2 \end{cases}$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 2

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm