10 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 8

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 8

6692 lượt thi
10 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giải phương trình $3 (x - 1) = 5 x + 2$

Xem đáp án

$3 (x - 1) = 5 x + 2$

$\Leftrightarrow 3 x - 3 = 5 x + 2 \Leftrightarrow 5 x - 3 x = - 3 - 2 \Leftrightarrow 2 x = - 5 \Leftrightarrow x = \frac{- 5}{2}$

Câu 2:

Cho biểu thức $A = \sqrt{x + 2 \sqrt{x - 1}} + \sqrt{x - 2 \sqrt{x - 1}},$ với $x \geq 1$

Tính giá trị của biểu thức A khi x =5

Xem đáp án

a) Điều kiện $x \geq 1$

Khi $x = 5 (t m ... x \geq 1)$ thay vào biểu thức ta được:

$\begin{array}{l} A = \sqrt{5 + 2 \sqrt{5 - 1}} + \sqrt{5 - 2 \sqrt{5 - 1}} = \sqrt{5 + 2 \sqrt{4}} + \sqrt{5 - 2 \sqrt{4}} \\ = \sqrt{5 + 2.2} + \sqrt{5 - 2.2} = \sqrt{9} + \sqrt{1} = 3 + 1 = 4 \end{array}$

Vậy khi x=5 thì A=4

Câu 3:

b,Rút gọn biểu thức A khi $1 \leq x \leq 2$

Xem đáp án

b) Điều kiện $1 \leq x \leq 2$

$\begin{array}{l} A = \sqrt{x + 2 \sqrt{x - 1}} + \sqrt{x - 2 \sqrt{x - 1}} \\ = \sqrt{x - 1 + 2 \sqrt{x - 1} + 1} + \sqrt{x - 1 - 2 \sqrt{x - 1} + 1} \\ = \sqrt{{(\sqrt{x - 1} + 1)}^{2}} + \sqrt{{(\sqrt{x - 1} - 1)}^{2}} \\ = |\sqrt{x - 1} + 1| + |\sqrt{x - 1} - 1| \\ = \sqrt{x - 1} + 1 + 1 - \sqrt{x - 1} (1 \leq x \leq 2 \Rightarrow 0 \leq \sqrt{x - 1} \leq 1 \Rightarrow \sqrt{x - 1} - 1 \leq 0) \\ = 2 \end{array}$

Câu 4:

1. Cho phương trình : $x^{2} - (m - 1) x - m = 0.$ Tìm m để phương trình có một nghiệm bằng 2. Tính nghiệm còn lại

Xem đáp án

Thay nghiệm x= 2 vào phương trình ta được:

$2^{2} - (m - 1) .2 - m = 0 \Leftrightarrow 4 - 2 m + 2 - m = 0 \Leftrightarrow 3 m = 6 \Leftrightarrow m = 2$

Thay m= 2 vào phương trình ta được: $x^{2} - x - 2 = 0 \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 2 \end{array}$

Vậy với m=2 phương trình đã cho có 1 nghiệm bằng 2, nghiệm còn lại x=-1

Câu 5:

Trong mặt phẳng tọa độ Oxy cho ba đường thẳng $d_{1} : y = 2 x - 1; d_{2} : y = x;$

$d_{3} : y = - 3 x + 2.$ Tìm hàm số có đồ thị là đường thẳng $d / / d_{3}$ đồng thời đi qua giao điểm của hai đường thẳng $d_{1}$ và $d_{2}$

Xem đáp án

Gọi phương trình đường thẳng $d : y = a x + b (a, b \in ℝ)$

Đường thẳng $d / / d_{3} \Rightarrow \{\begin{cases} a = - 3 \\ b \neq 2 \end{cases} \Rightarrow d : y = - 3 x + b (b \neq 2)$

Tọa độ giao điểm của hai đường thẳng $d_{1}, d_{2}$ là nghiệm của hệ phương trình:

$\{\begin{cases} y = 2 x - 1 \\ y = x \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 1 \end{cases} \Rightarrow A (1; 1)$

Đường thẳng $d : y = - 3 x + b$ đi qua giao điểm của hai đường thẳng $d_{1}, d_{2}$ nên d đi qua $A (1; 1)$

Thay tọa độ điểm $A (1; 1)$ vào phương trình đường thẳng d ta được:

$1 = - 3.1 + b \Leftrightarrow b = 4 (t m)$

Vậy phương trình đường thẳng cần tìm là $d : y = - 3 x + 4$

Câu 6:

Hai đội công nhân cùng làm chung trong 4 giờ thì hoàn thành được $\frac{2}{3}$ công việc. Nếu làm riêng thì thời gian hoàn thành công việc đội thứ hai ít hơn đội thứ nhất là 5 giờ. Hỏi nếu làm riêng thì thời gian hoàn thành công việc của mỗi đội là bao nhiêu

Xem đáp án

Gọi thời gian làm riêng hoàn thành công việc của đội là x (giờ) $(x > 5)$

Vì nếu làm riêng thì thời gian hoàn thàn công việc đội thứ hai ít hơn đội thứ nhất 5 giờ

Nên thời gian đội 2 làm riêng để hoàn thành công việc là 5 giờ

Trong 1 giờ đội thứ nhất làm riêng được x-5 (công việc)

Trong 4 giờ đội thứ nhất làm được $\frac{1}{x}$ (công việc)

Trong 4 giờ đội thứ hai làm được $\frac{4}{x - 5}$ (công việc)

Trong 4 giờ cả hai đội làm được: $\frac{4}{x} + \frac{4}{x - 5} = \frac{2}{3}$ (công việc)

Giải phương trình

$\begin{array}{l} \frac{4}{x} + \frac{4}{x - 5} = \frac{2}{3} \Leftrightarrow 4. (\frac{1}{x} + \frac{1}{x - 5}) = \frac{2}{3} \\ \Leftrightarrow \frac{1}{x} + \frac{1}{x - 5} = \frac{1}{6} \Leftrightarrow \frac{x - 5 + x}{x (x - 5)} = \frac{1}{6} \\ \Leftrightarrow 12 x - 30 = x^{2} - 5 x \Leftrightarrow x^{2} - 17 x + 30 = 0 \\ \Leftrightarrow (x - 2) (x - 15) = 0 \Leftrightarrow [\begin{array}{l} x = 2 (k t m) \\ x = 15 (t m) \end{array} \end{array}$

Vậy thời gian hoàn thành công việc của đội I là 15 giờ, của đội II là 10 giờ

Câu 7:

Cho (O;R) và một đường thẳng (d) không cắt (O). Dựng đường thẳng $O H ⊥ d$ tại điểm H. Trên đường thẳng d lấy điểm K (K khác H), qua K vẽ hai tiếp tuyến $K A, K B$ với (O), (A, B là tiếp điểm) sao cho $A, H$ nằm về hai phía của đường thẳng OK

Chứng minh tứ giác KAOH nội tiếp

Xem đáp án

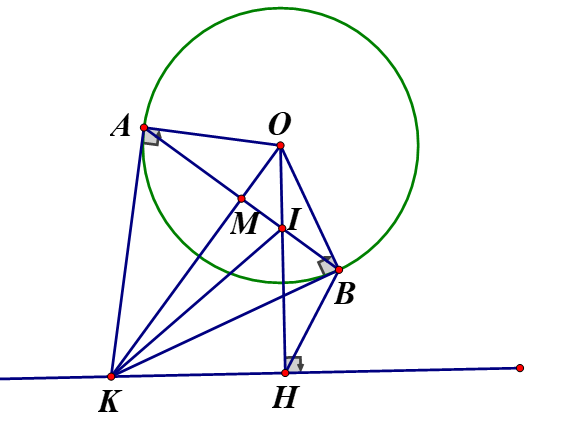
Cho (O;R) và một đường thẳng (d) không cắt (O). Dựng đường thẳng OH vuông góc d tại điểm H. (ảnh 1)

Vì KA là tiếp tuyến của (O) nên $A K ⊥ O A \Rightarrow \hat{K A O} = 90^{0}$

Lại có : $\hat{O H K} = 90^{0} ($ do $O H ⊥ d)$

Xét tứ giác AOKH có $\hat{O A K} + \hat{O H K} = 90^{0} + 90^{0} = 180^{0}$ mà 2 góc ở vị trí đối nhau nên OAKH là tứ giác nội tiếp (dhnb)

Câu 8:

b, Đường thẳng AB cắt đường thẳng OH tại I. CMR: $I A . I B = I H . I O$ và I là điểm cố định khi điểm K chạy trên đường thẳng d cố định

Khi $O K = 2 R, O H = R \sqrt{3} .$ Tính diện tích $Δ K A I$ theo R

Xem đáp án

Xét (O) có $\hat{O B K} = 90^{0}$ (do KB là tiếp tuyến của đường tròn (O))

Từ đó ta có: $\hat{O A K} = \hat{O B K} = \hat{O H K} = 90^{0}$ nên 5 điểm $A, O, B, H, K$ cùng thuộc đường tròn đường kính OK $\Rightarrow \hat{O A B} = \hat{O H B}$ (hai góc nội tiếp cùng chắn cung OB)

Xét $Δ I O A$ và $Δ I B H$ có: $\hat{O I A} = \hat{B I H}$ (hai góc đối đỉnh), $\hat{O A B} = \hat{O H B} (c m t)$

$\Rightarrow Δ I O A ~ Δ I B H (g . g) \Rightarrow \frac{I O}{I B} = \frac{I A}{I H} \Leftrightarrow I O . I H = I A . I B$

Xét đường tròn đường kính OK có

$\hat{O H B}$ là góc nội tiếp chắn cung OB

$\hat{O B A}$ là góc nội tiếp chắn cung OA

$\Rightarrow \hat{O H B} = \hat{O B A}$ (hai góc nội tiếp chắn hai cung bằng nhau)Mà $O A = O B = R$

Xét $Δ O I B$ và $Δ O B H$ có:

$\hat{B O H}$ chung; $\hat{O H B} = \hat{O B A} (c m t)$

$\Rightarrow Δ O I B ~ Δ O B H (g . g) \Rightarrow \frac{O I}{O B} = \frac{O B}{O H} \Leftrightarrow O I = \frac{O B^{2}}{O H}$

Mà đường thẳng d cố định nên OH không đổi vì $O H ⊥ d$

$\Rightarrow O I = \frac{R^{2}}{O H}$ không đổi hay điểm I cố định khi K chạy trên đường thẳng d cố định

Câu 9:

c, Khi $O K = 2 R, O H = R \sqrt{3} .$ Tính diện tích $Δ K A I$ theo R

Xem đáp án

Gọi M là giao điểm của $O K, A B$

Xét (O) có KA, KB là hai tiếp tuyến nên KA=KB

Lại có $O A = O B = R$ nên OK là đường trung trực của AB suy ra $A B ⊥ O K$ tại M

$\Rightarrow S_{A K I} = \frac{1}{2} A I . K M$

Theo câu b) ta có: $O I = \frac{R^{2}}{O H} = \frac{R^{2}}{R \sqrt{3}} = \frac{R}{\sqrt{3}}$

Xét tam giác OAK vuông tại A, theo hệ thức lượng trong tam giác vuông ta có:

$O A^{2} = O M . O K \Leftrightarrow O M = \frac{O A^{2}}{O K} = \frac{R^{2}}{2 R} = \frac{R}{2}$

Suy ra $K M = O K - O M = 2 R - \frac{R}{2} = \frac{3 R}{2}$

$A M^{2} = O M . K M = \frac{R}{2} . \frac{3 R}{2} = \frac{3 R^{2}}{4} \Rightarrow A M = \frac{R \sqrt{3}}{2}$

Xét tam giác OMI vuông tại M, theo định lý Pytago, ta có:

$M I = \sqrt{O I^{2} - O M^{2}} = \sqrt{{(\frac{R}{\sqrt{3}})}^{2} - {(\frac{R}{2})}^{2}} = \frac{R \sqrt{3}}{6}$

Suy ra $A I = A M + M I = \frac{R \sqrt{3}}{2} + \frac{R \sqrt{3}}{6} = \frac{2 R \sqrt{3}}{3}$

$\Rightarrow S_{K A I} = \frac{1}{2} K M . A I = \frac{1}{2} . \frac{3 R}{2} . \frac{2 R \sqrt{3}}{3} = \frac{R^{2} \sqrt{3}}{2}$

Vậy $S_{K A I} = \frac{R^{2} \sqrt{3}}{2}$

Câu 10:

Cho x, y là hai số thực thỏa $\{\begin{cases} x > y \\ x y = 1 \end{cases} .$ Tìm giá trị nhỏ nhất của biểu thức $P = \frac{x^{2} + y^{2}}{x - y}$

Xem đáp án

Với $x > y, x y = 1$ ta có:

$P = \frac{x^{2} + y^{2}}{x - y} = \frac{{(x - y)}^{2} + 2 x y}{x - y} = (x - y) + \frac{2}{x - y} \overset{C o s i}{\geq} 2 \sqrt{(x - y) \frac{2}{x - y}} = 1 (D o .. x > y \Rightarrow x - y > 0)$ Dấu “=” xảy ra $\Leftrightarrow x - y = \frac{2}{x - y} \Leftrightarrow {(x - y)}^{2} = 2 \Leftrightarrow x - y = \sqrt{2} \Rightarrow x = y + \sqrt{2}$

Mà $x y = 1 \Leftrightarrow (y + \sqrt{2}) y = 1 \Leftrightarrow y^{2} + \sqrt{2} y = 1 \Leftrightarrow y^{2} + \sqrt{2 y} - 1 = 0 \Leftrightarrow [\begin{array}{l} y = \frac{\sqrt{6} - \sqrt{2}}{2} (t m) \\ y = \frac{- \sqrt{6} - \sqrt{2}}{2} \end{array} ($

Khi đó $x = \frac{1}{y} = \frac{2}{\sqrt{6} - \sqrt{2}} = \frac{\sqrt{6} + \sqrt{2}}{2}$

Vậy giá tri nhỏ nhất của P là $2 \sqrt{2}$ tại $x = \frac{\sqrt{6} + \sqrt{2}}{2}; y = \frac{\sqrt{6} - \sqrt{2}}{2}$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 8

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm