12 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 12

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 12

6887 lượt thi
12 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Rút gọn biểu thức $A = \sqrt{5} (\sqrt{20} - 3) + \sqrt{45}$

Xem đáp án

$\begin{array}{l} a) A = \sqrt{5} . (\sqrt{20} - 3) + \sqrt{45} a \\ = \sqrt{5} . \sqrt{20} - 3 \sqrt{5} + \sqrt{9.5} \\ = \sqrt{100} - 3 \sqrt{5} + 3 \sqrt{5} \\ = 10 \end{array}$

Câu 2:

b, Chứng minh rằng: $\sqrt{24 + 16 \sqrt{2}} - \sqrt{24 - 16 \sqrt{2}} = 4 \sqrt{2}$

Xem đáp án

Ta có:

$V T = \sqrt{24 + 16 \sqrt{2}} - \sqrt{24 - 16 \sqrt{2}}$

$= \sqrt{16 + 2.4.2 \sqrt{2} + 8} - \sqrt{16 - 2.4.2 \sqrt{2} + 8}$

$= \sqrt{{(4 + 2 \sqrt{2})}^{2}} - \sqrt{{(4 - 2 \sqrt{2})}^{2}}$

$= 4 + 2 \sqrt{2} - |4 - 2 \sqrt{2}|$

$= 4 + 2 \sqrt{2} - (4 - 2 \sqrt{2}) (d o 4 - 2 \sqrt{2} > 0)$

$= 4 + 2 \sqrt{2} - 4 + 2 \sqrt{2}$

$= 4 \sqrt{2} = V P (d f c m)$

Câu 3:

c, Tìm tập hợp các giá trị của x sao cho $\sqrt{2 x + 1} \leq 5$

Xem đáp án

c) Điều kiện: $2 x + 1 \geq 0 \Leftrightarrow x \geq - \frac{1}{2}$

Khi đó , bất phương trình đề $\Leftrightarrow 2 x + 1 \leq 25$

$\Leftrightarrow 2 x \leq 24 \Leftrightarrow x \leq 12$

Kết hợp với điều kiện, ta có: $- \frac{1}{2} \leq x \leq 12$

Câu 4:

a, Giải phương trình $\sqrt{x^{2} - 4 x + 4} + x = 8$

Xem đáp án

a, Ta có: $x^{2} - 4 x + 4 = {(x - 2)}^{2}$

Điều kiện: ${(x - 2)}^{2} \geq 0$ luôn đúng với mọi $x \in ℝ$

$\begin{array}{l} \sqrt{x^{2} - 4 x + 4} + x = 8 \Leftrightarrow \sqrt{{(x - 2)}^{2}} + x = 8 (*) \\ \Leftrightarrow |x - 2| + x = 8 \end{array}$

Nếu $x - 2 \geq 0$ thì $x \geq 2 \Rightarrow |x - 2| = x - 2$

Khi đó phương trình (*) trở thành: $x - 2 + x = 8 \Leftrightarrow x = 5 (t m)$

Nếu $x - 2 < 0 \Leftrightarrow x < 2 \Rightarrow |x - 2| = - x + 2$

Khi đó, phương trình (*) trở thành $- x - 2 + x = 8 \Leftrightarrow - 2 = 8$ (vô lý)

Vậy tập nghiệm của phương trình đã cho là $S = \{5\}$

Câu 5:

Giải hệ phương trình: $\{\begin{cases} x + y = 4 \\ 2 x - y = - 7 \end{cases}$

Xem đáp án

$b) \{\begin{cases} x + y = 4 \\ 2 x - y = - 7 \end{cases} \Leftrightarrow \{\begin{cases} 3 x = - 3 \\ x + y = 4 \end{cases} \Leftrightarrow \{\begin{cases} x = - 1 \\ y = 4 - x \end{cases} \Leftrightarrow \{\begin{cases} x = - 1 \\ y = 5 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất $(x; y) = (- 1; 5)$

Câu 6:

Cho phương trình $x^{2} - 2 (m + 2) x + m + 1 = 0$ (x là ẩn)

Giải phương trình khi $m = - \frac{3}{2}$

Xem đáp án

Thay $m = - \frac{3}{2}$ vào phương trình đã cho ta được:

$\begin{array}{l} x^{2} - 2. (\frac{- 3}{2} + 2) x - \frac{3}{2} + 1 = 0 \\ \Leftrightarrow x^{2} - 2. \frac{1}{2} x - \frac{1}{2} = 0 \\ \Leftrightarrow x^{2} - x - \frac{1}{2} = 0 (*) \\ Δ = 1^{2} - 4.1. (- \frac{1}{2}) = 3 > 0 \Rightarrow \sqrt{Δ} = \sqrt{3} \end{array}$

Phương trình (*) có 2 nghiệm phân biệt $x_{1} = \frac{1 + \sqrt{3}}{2}; x_{2} = \frac{1 - \sqrt{3}}{2}$

Câu 7:

b, Chứng minh rằng phương trình luôn có hai nghiệm phân biệt

Xem đáp án

Phương trình $x^{2} - 2 (m + 2) x + m + 1 = 0$ (x là ẩn)

$\begin{array}{l} Δ' = {(m + 2)}^{2} - 1 (m + 1) \\ = m^{2} + 4 m + 4 - m - 1 \\ = m^{2} + 3 m + 3 \\ = (m^{2} + 2. m . \frac{3}{2} + \frac{9}{4}) + \frac{3}{4} \end{array}$

$Δ' = {(m + \frac{3}{2})}^{2} + \frac{3}{4} > 0$ với mọi m

Vậy phương trình đã cho luôn có 2 nghiệm phân biệt

Câu 8:

Gọi $x_{1}; x_{2}$ là hai nghiệm của phương trình. Tìm các giá trị của m để $x_{1}^{2} + x_{2}^{2} = 8$

Xem đáp án

Phương trình $x^{2} - 2 (m + 2) x + m + 1 = 0$ luôn có hai nghiệm phân biệt

Áp dụng hệ thức Viet ta có: $\{\begin{cases} x_{1} + x_{2} = 2 (m + 2) = 2 m + 4 \\ x_{1} x_{2} = m + 1 \end{cases}$

Theo đề, ta có: $x_{1}^{2} + x_{2}^{2} = 8 \Leftrightarrow {(x_{1} + x_{2})}^{2} - 2 x_{1} x_{2} = 8$

$\begin{array}{l} \Rightarrow {(2 m + 4)}^{2} - 2 (m + 1) = 8 \\ \Leftrightarrow 4 m^{2} + 16 m + 16 - 2 m - 2 = 8 \\ \Leftrightarrow 4 m^{2} + 14 m + 6 = 0 \\ \Leftrightarrow 2 m^{2} + 7 m + 3 = 0 \\ \Leftrightarrow (2 m^{2} + 6 m) + (m + 3) = 0 \\ \Leftrightarrow 2 m (m + 3) + (m + 3) = 0 \\ \Leftrightarrow (2 m + 1) (m + 3) = 0 \\ \Leftrightarrow [\begin{array}{l} 2 m + 1 = 0 \\ m + 3 = 0 \end{array} \Leftrightarrow [\begin{array}{l} m = - \frac{1}{2} \\ m = - 3 \end{array} \end{array}$

Vậy $m = - 3, m = - \frac{1}{2}$ thỏa mãn yêu cầu bài toán

Câu 9:

Hai đội công nhân cùng làm một công việc thì xong trong 4 giờ. Nếu mỗi đội làm riêng xong được công việc ấy, thì đội thứ hai cần nhiều hơn đội thứ nhất là 6 giờ. Hỏi mỗi đội làm riêng xong công việc ấy trong bao lâu ?

Xem đáp án

Gọi thời gian làm riêng công việc của đội thứ nhất là x (giờ) $x > 0$

Thời gian làm riêng xong công việc của đội thứ hai là x +6 (giờ)

Trong 1 giờ, đội thứ nhất làm được : $\frac{1}{x}$ (công việc)

Trong 1 giờ, đội thứ hai làm được: $\frac{1}{x + 6}$ (công việc)

Hai đội cùng làm một công việc thì xong trong 4 giờ nên ta có:

$\begin{array}{l} 4. (\frac{1}{x} + \frac{1}{x + 6}) = 1 \Leftrightarrow \frac{1}{x} + \frac{1}{x + 6} = \frac{1}{4} \\ \Leftrightarrow \frac{4. (x + 6)}{4 x (x + 6)} + \frac{4 x}{4 x (x + 6)} = \frac{x (x + 6)}{4 x (x + 6)} \\ \Rightarrow 4. (x + 6) + 4 x = x (x + 6) \Leftrightarrow 4 x + 24 + 4 x = x^{2} + 6 x \\ \Leftrightarrow x^{2} + 6 x - 4 x - 24 - 4 x = 0 \Leftrightarrow x^{2} - 2 x - 24 = 0 \\ \Leftrightarrow x^{2} - 6 x + 4 x - 24 = 0 \Leftrightarrow x (x - 6) + 4 (x - 6) = 0 \\ \Leftrightarrow (x + 4) (x - 6) = 0 \Leftrightarrow [\begin{array}{l} x = - 4 (k t m) \\ x = 6 (t m) \end{array} \end{array}$

Vậy đội thứ nhất làm riêng xong công việc trong 6 giờ, đội thứ hai làm riêng xong công việc trong 12 giờ.

Câu 10:

Cho tam giác ABC vuông tại A (AB> AC) , đường cao AH. Trên đoạn HC lấy điểm D sao cho DH= DB vẽ CE vuông góc với $A D (E \in A D) .$

Chứng minh tứ giác AHEC nội tiếp, xác định tâm O của đường tròn ngoại tiếp tứ giác AHEC

Xem đáp án

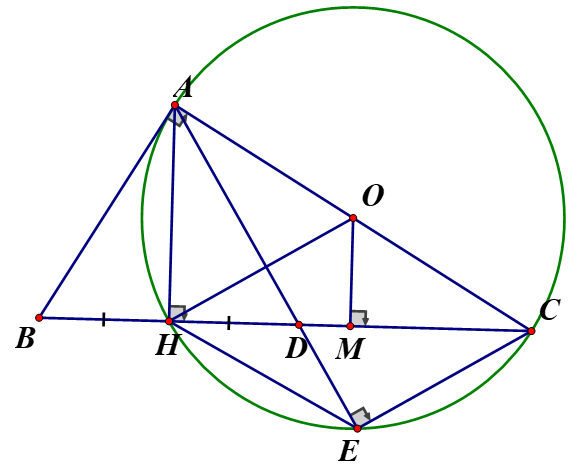
Cho tam giác ABC vuông tại A (AB> AC) , đường cao AH. (ảnh 1)

Ta có: $\hat{A H C} = 90^{0}$ (vì $A H ⊥ B C)$ và $\hat{A E C} = 90^{0}$ (vì $A E ⊥ E C)$

Xét tứ giác AHCE có E, H là hai đỉnh kề nhau cùng nhìn cạnh AC dưới một góc $α = 90^{0}$ $(\hat{A H C} = \hat{A E C} = 90^{0})$

Suy ra tứ giác AHCE là tứ giác nội tiếp . Tâm O của đường tròn ngoại tiếp tứ giác AHCE là trung điểm của cạnh AC.

Câu 11:

b, Chứng minh CH là tia phân giác của $\hat{A C E}$

Xem đáp án

Vì tứ giác AHEC là tứ giác nội tiếp nên:

$\hat{A C H} = \frac{1}{2} s d \overset{⏜}{A H}$ (hai góc nội tiếp cùng chắn cung AH) (1)

Theo câu a, tứ giác AHEC nội tiếp đường tròn đường kính AC.

Theo đề bài: $\hat{B A C} = 90^{0}$ (Vì $Δ A B C$ vuông tại A)

$\Rightarrow A B$ là tiếp tuyến của đường tròn tâm O, đường kính AC.

$\Rightarrow \hat{B A H} = \frac{1}{2} s d \overset{⏜}{A H}$ (góc tạo bởi tia tiếp tuyến và dây cung ) (2)

Từ (1) và (2) suy ra $\hat{A C H} = \hat{B A H} (3)$

Vì tứ giác AHEC là tứ giác nội tiếp nên:

$\hat{E A H} = \hat{E C H} = \frac{1}{2} s d \overset{⏜}{E H}$ (hai góc nội tiếp cùng chắn cung AH ) (4)

Xét $Δ A B D$ có AH là đường cao, đồng thời là đường trung tuyến nên $Δ A B D$ cân tại A $\Rightarrow A H$ là phân giác của $\hat{B A D} \Rightarrow \hat{B A H} = \hat{E A H} (5)$

Từ (3), (4), (5) suy ra $\hat{A C H} = \hat{E C H}$

Vậy CH là tia phân giác của $\hat{A C E}$

Câu 12:

c,Tính diện tích giới hạn bởi đoạn thẳng CA, CH và cung nhỏ AH của đường tròn ngoại tiếp tứ giác AHEC Biết $C A = 6 c m, \hat{A C B} = 30^{0} .$

Xem đáp án

Gọi diện tích hình quạt tròn AOH là $S_{q} = \frac{π R^{2} . \hat{A O H}}{360^{0}}$

Diện tích cần tính là: $S_{q} + S_{O H C}$

Theo đề bài , $A C = 6 c m,$ O là trung điểm của AC

$\Rightarrow O A = O C = R = 3 c m$

Ta lại có: $O H = O C = R = 3 c m \Rightarrow Δ O H C$ cân tại O

$\Rightarrow \hat{O H C} = \hat{O C H} = 30^{0}$ (vì $\hat{A C B} = 30^{0})$

$\Rightarrow \hat{A O H} = \hat{O H C} + \hat{O C H} = 30^{0} + 30^{0} = 60^{0}$ (góc ngoài của tam giác)

$S_{q} = \frac{π {.3}^{2} {.60}^{0}}{360^{0}} = \frac{π {.3}^{2}}{6} = \frac{3}{2} π (c m^{2})$

Gọi M là trung điểm của HC

$\Rightarrow O M ⊥ H C$ (tính chất đường kính dây cung)

$S_{O H C} = \frac{1}{2} O M . H C$

Xét $Δ A H C$ vuông tại H có:
$\cos \hat{A C H} = \frac{H C}{A C} \Rightarrow H C = A C . \cos \hat{A C H} = A C . \cos 30^{0} = 6. \frac{\sqrt{3}}{2} = 3 \sqrt{3} (c m)$

Vì M là trung điểm của $H C \Rightarrow H M = \frac{H C}{2} = \frac{3 \sqrt{3}}{2}$

Xét $Δ O M H$ vuông tại M, theo định lý Pytago ta có: $O H^{2} = O M^{2} + M H^{2}$

$\begin{array}{l} \Rightarrow O M^{2} = O H^{2} - M H^{2} = 3^{2} - {(\frac{3 \sqrt{3}}{2})}^{2} \\ O M^{2} = 9 - \frac{27}{4} = \frac{9}{4} \Rightarrow O M = \sqrt{\frac{9}{4}} = \frac{3}{2} (c m) \end{array}$

$S_{O H C} = \frac{1}{2} . O M . H C = \frac{1}{2} . \frac{3}{2} .3 \sqrt{3} = \frac{9 \sqrt{3}}{4} (c m^{2})$

Diện tích cần tính là : $S_{q} + S_{O H C} = \frac{3}{2} π + \frac{9 \sqrt{3}}{4} = \frac{9 \sqrt{3} + 6 π}{4} (c m^{2})$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 12

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm